矩形覆盖

矩形覆盖

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

比如n=3时，2*3的矩形块有3种覆盖方法：

这又是一个斐波那契，重要的是思路:

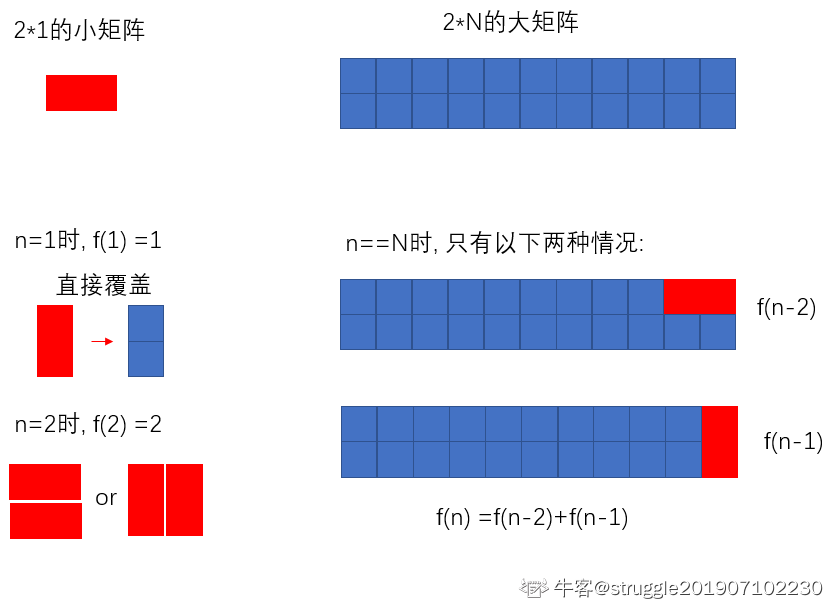
其实严格来说，斐波那契数列问题是动态规划问题的一种特殊情况，所以其实其也属于动态规划问题

---

上面是宽度为2的情况，那么宽度为三呢？

http://noi.openjudge.cn/ch0405/1665/

1665:完美覆盖

• 查看

• 提交

• 统计

• 提问

• 总时间限制:

  1000ms

• 内存限制:

  65536kB

• 描述

  一张普通的国际象棋棋盘，它被分成 8 乘 8 (8 行 8 列) 的 64 个方格。设有形状一样的多米诺牌，每张牌恰好覆盖棋盘上相邻的两个方格，即一张多米诺牌是一张 1 行 2 列或者 2 行 1 列的牌。那么，是否能够把 32 张多米诺牌摆放到棋盘上，使得任何两张多米诺牌均不重叠，每张多米诺牌覆盖两个方格，并且棋盘上所有的方格都被覆盖住？我们把这样一种排列称为棋盘被多米诺牌完美覆盖。这是一个简单的排列问题，同学们能够很快构造出许多不同的完美覆盖。但是，计算不同的完美覆盖的总数就不是一件容易的事情了。不过，同学们 发挥自己的聪明才智，还是有可能做到的。 现在我们通过计算机编程对 3 乘 n 棋盘的不同的完美覆盖的总数进行计算。 任务 对 3 乘 n 棋盘的不同的完美覆盖的总数进行计算。

• 输入

  一次输入可能包含多行，每一行分别给出不同的 n 值 ( 即 3 乘 n 棋盘的列数 )。当输入 -1 的时候结束。 n 的值最大不超过 30.

• 输出

  针对每一行的 n 值，输出 3 乘 n 棋盘的不同的完美覆盖的总数。

• 样例输入

  2 8 12 -1

• 样例输出

  3 153 2131

---

思路：

设 a[i] 为 N=i 时的方法数. i 为奇数的时候肯定为 0.

如果 i 为偶数, a[i] 可以看成 a[i-2] 加上两个单位组成的, 此时多出来的 2 单位有 3 种方法..

也可以看成 a[i-4] 加上四个单位组成的, 此时这四个单位一定是连在一起的, 中间不能分割, 所以只有两种放法.

同理, 可看成 a[i-6] 加上六个单位组成的, 此时这六个单位也连在一起, 不能分割, 只有两种放法…

直到所有的砖块都是连在一起的, 中间不能分割, 也只有两种放法.

所以
a[i]=3*a[i-2]+2*(a[i-4]+a[i-6]+…+a[0]) ①

a[i-2]=3*a[i-4]+2*(a[i-6]+…a[0]) ②

①-②, 得 a[i]=4*a[i-2]-a[i-4].

---

这里有一点关键的，就是我在分析的时候犯了一个错误：

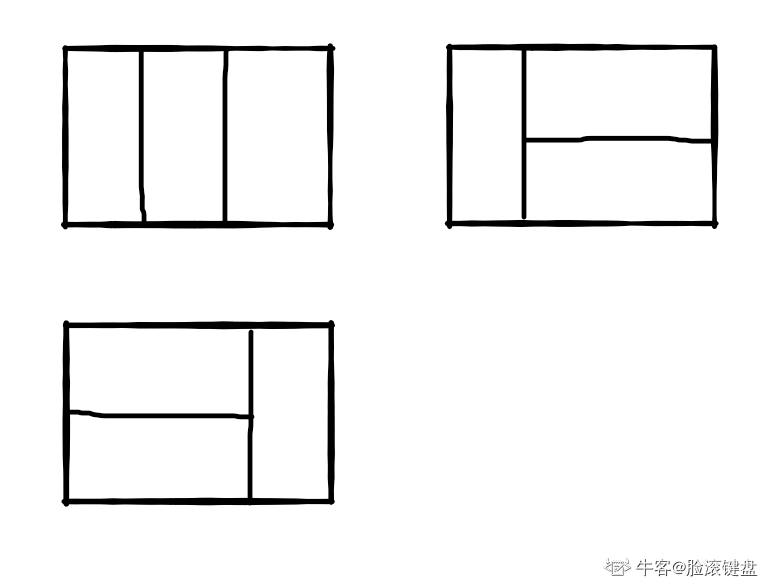
分析6个单位的情况时，我以为有四种情况，分别是:

但是其实这里我犯了个错误，就是后面两种情况其实是两个单位的情况，而不是六个！所以最后分析上出现了失误

按原思路来，其就变成了一个动态规划问题。

另外，原思路中对式子进行消元的思路很好，如果只拿着①式做的话需要不断地求数列和，而消元后只需要求两项和了

---

package com.jiading.noi;

import java.util.Scanner;


/*
 * 1665:完美覆盖
 * http://noi.openjudge.cn/ch0405/1665/
 */
public class Problem30 {
//a[i]=4*a[i-2]-a[i-4].
	public static void main(String[] args) {
		Scanner scanner=new Scanner(System.in);
		int largestN=0;
		int[]largestDp=null;
		while(true) {
			Integer n=scanner.nextInt();
			if(n.equals(-1)) {
				return;
			}
            //没什么原因，oj平台要求的
			if(n.equals(0)) {
				System.out.println(1);
				continue;
			}
			//不可能是奇数，所以奇数的话可以直接返回是0
			if(n<0||n%2==1) {
				System.out.println(0);
				continue;
			}
			if(n.equals(2)) {
				System.out.println(3);
				continue;
			}
			if(n.equals(4)) {
				System.out.println(11);
				continue;
			}
			if(n>largestN) {
				int[]dp=new int[n+1];
				dp[2]=3;
				dp[4]=11;
				for(int i=6;i<=n;i+=2) {
					dp[i]=4*dp[i-2]-dp[i-4];
				}
				System.out.println(dp[n]);
				largestN=n;
				largestDp=dp;
			}else {
				System.out.println(largestDp[n]);
			}
		}
	}
}

注意这里我设置了一个largestDp!，它可以在多次输入n，也就是多次计算该动态规划问题时复用之前计算出来的dp数组，默认只保留最大的dp数据，如果需要更大的则重新计算并保存该计算结果，这可以省不少时间

还有一个思路是，因为这里限定了N最大是30，所以可以先把30的算出来，从而之后n是几都可以直接拿，避免重复计算，也是一个很好的思路