求素数

求素数 - 普通方法

void s12_2()
{
    //求素数 - 普通方法
    const int MAX2=100; 
    bool a[MAX2+10];                    //全局数组，初始值均为false即0
    int prime[MAX2],Count=0;            //prime存素数,Count统计素数个数
    for (int i=2; i<=MAX2; i++)
    {
      if (a[i]==0)                   //a[i]=0表示是素数
        prime[Count++]=i;            //素数依次存入prime[]
      if(i<=sqrt(MAX2))               //不要写成i*i<=MAX,防止i*i过大溢出
        for (int j=i*i; j<=MAX2; j+=i)//从i*i开始，因为i*(2~i-1)已删除
          a[j]=1;                    //标记a[j]不是素数
    }
    for (int i=0; i<Count; i++)
      cout<<prime[i]<<' ';
} 

 

 

 

 

 

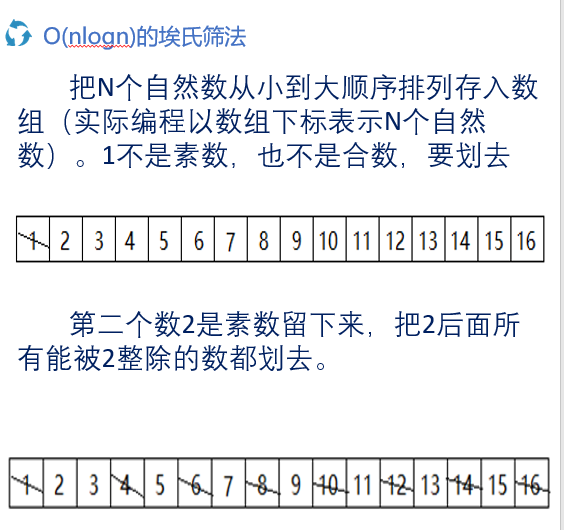
const int MAX1=100;
void s12()
{
    //O(nlogn)的埃氏筛法 
    bool a[MAX1+10]={0};                    //全局数组，初始值均为false即0
    int prime[MAX1],Count=0;            //prime存素数,Count统计素数个数
    int limit=sqrt(MAX1);    
     for (int i=2; i<=MAX1; i++)
     {
         if (a[i]==0)                   //a[i]=0表示是素数
         {
             prime[Count++]=i;            //素数依次存入prime[]
        }
        if(i<limit)               //不要写成i*i<=MAX,防止i*i过大溢出
        {
              for (int j=i*i; j<=MAX1; j+=i)//从i*i开始，因为i*(2~i-1)已删除
              {
                   a[j]=1;                    //标记a[j]不是素数
              }
        }        
     }
     for (int i=0; i<Count; i++)
     {
         cout<<prime[i]<<' ';
     }
     cout<<endl;    
} 

 

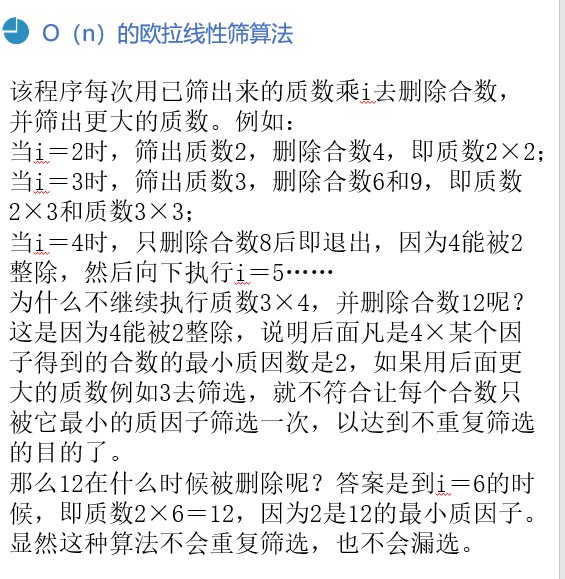
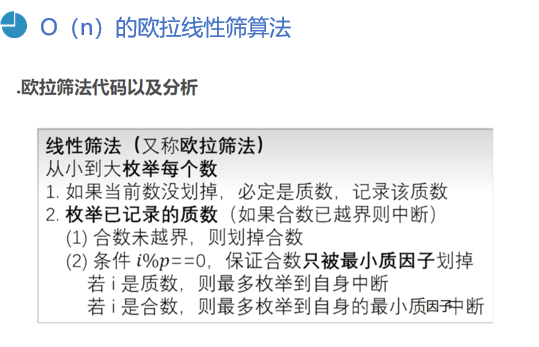
void s12_1()
{
    //欧拉线性筛算法
    const int MAXN = 100;
    bool a[MAXN];                   //a[i]=0表示i是质数
    int prime[MAXN/3], Count;       //prime[N]保存质数,Count:找到的质数个数
    for(int i=2; i<MAXN; i++)
    {
      //从小到大枚举每个数    
      if(a[i]==0)
        prime[Count++] = i;       //质数依次存起来
      for(int j=0; j<Count && i*prime[j]<MAXN; j++)
      {
          //枚举已记录的质数 
        a[i*prime[j]]=1;          //合数未越界，记录合数 
        if(i%prime[j] == 0)       //此处是优化的关键
        {
          /*
          若i为质数，则最多枚举到自身中断
          若i为合数，则最多枚举到自身的最小质因数中断 
          */ 
          break;                  //保证每个合数被它最小的质因数筛去
        } 
      }
    }
    for(int i=0; i<Count; i++)
      cout<<prime[i]<<' ';
    //cout<<prime[Count-1]<<endl;
}