浅谈STM32-ADC之基本组成及原理（1）

在使用STM32编写ADC时，我们要先了解下ADC的A/D转换器。

ADC相关篇幅中，主要是关于ADC如何使用的相关内容，然而学习总是有一个循序渐进的过程，在不了解ADC之前，强硬的训练实现熟练应用，太过于强求。

因此在学习ADC之前，重新翻看了数电中关于A/D转换的相关基础知识。

1.前因后果

由于计算机在自动控制，自动检测以及许多其他领域广泛应用数字电子技术(我们使用的计算机本质就是数字计算机)。但是并不是多有信号都是数字信号，有些是模拟信号。为了能够使用数字电路处理模拟信号，所以出现了：模拟信号转换成相应的数字信号（模——数转换，A/D）,和数字信号转换成相应的模拟信号（数——模转换，D/A）.

2.如何转换的呢（A/D转换的基本原理）

（1）首先在一个选定的瞬间对模拟信号进行采样。（2）然后再将取样值转换成数字量。（3）按照一定的编码格式给出转换结果。

3.反思

这三个步骤，看上去并没有啥问题。但是真的没有吗？试想一下，对于一个规律变化的正弦波，如果采样分别出现在正最大值和负最大值，那么同一个波形，根据这两个极端的采样，经转换得到的两个数字量，是千差万别的。

接下来的（1）（2）（3）将是对上面（《2如何转换的》中的（1）（2）（3）的具体解释）。

（1）因此说明对于采样是有一定讲究的。如下图：

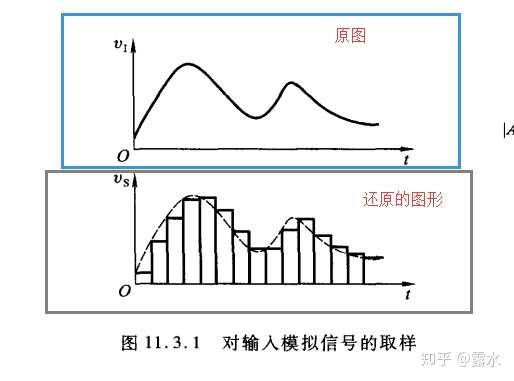
需要明确一件事：采样决不是采一个点。而是许多点。如果在某一个时间段，采样的个数足够多，换句话说，就是长方形最够又长又细，已经接近一条竖线，那么我将这些长方形拼接起来就是原来的波形。

上面一句话中，有一句黑体加粗文字：“如果再某一个时间段，采取的个数足够多”。这句话其实就是频率的事情，在一个固定的时间段中采样次数越多，那么采样的频率也就越快。

上图中原图的波形的最大频率如果是  ,然而如果采样的频率比原图波形最大频率的2倍还要大。那么将采样的所有样本拼接在一起，将可以正确无误的表达原图的波形（这就是采样定理）。

（2）将取样值转换成数字量也需要一定的标准（参考标准）。我们在表达一个数字量大小的时候，必须要有一个最小数量单位（标准）。其他数字量都是这个最小单位的整数倍。因此我们在进行量化的过程中不可避免的就存在了误差。如下图

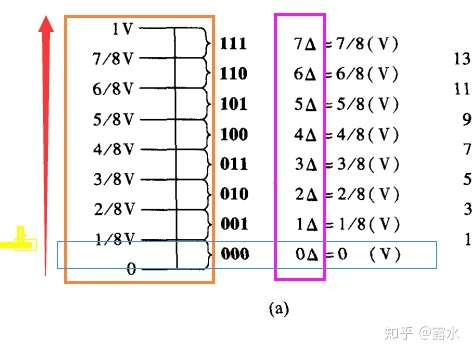
从0V-1V是一个连续的电压量。然而0-  统一被认定为0  .势必存在误差（  是最小基本单位）。

（3）按照一定的编码格式给出转换结果，这个很容易理解，是二进制，八进制，十进制，还是十六进制。

4.举例

举两个A/D转换器的例子：（1）计数型反馈比较型A/D转换器

如下图

 

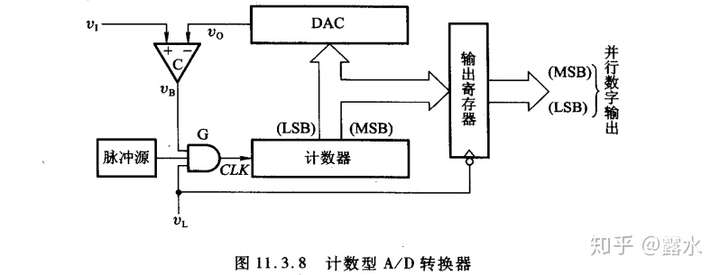
为了理清楚转换器转换的思路，不在过多介绍细节。主要步骤如下：

（1）  从低电平变为高电平，从而脉冲源发出的脉冲经过G加到CLK上。计数器加1

（2）将这个计数器数值 送到DAC中，转换为一个模拟信号  .

（3） 和  比较，如果小于 继续重复（1）（2）。直到俩信号相等为止，这里 就是我们想要转换的模拟量（就是模数转换的目的就是想把他转换成数字量，换句话说我们在转换器中输入一个模拟量，经转换输出一个数字量，那么这个输入的模拟量就是）。这里是通过计数器不断的加1加1.生成一个和 一样的模拟量。如果 = .那么计数器的值，也就自然而然等于 转换成数字量的值了。（因为计数器中的值经过数模转换转换成了 ，= 所以， 经转换，转换成数字量当然等于计数器的值）

（4）将 = 时，计数器的值送到输出寄存器，这就是果 转换成的数字量

 

 

 

举例（2）逐次渐近型A/D转换器

如下图

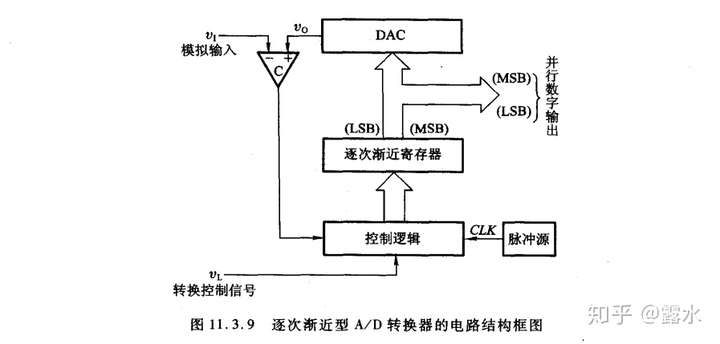
同理为了理清楚转换的思路，不再过多介绍电路细节。步骤如下：

（1）控制信号  从低电平变为高电平。脉冲产生CLK。

（2）逐次渐近寄存器最高位（就像一个字节8位的最高位）变为1.

（3）将这个寄存器中的数送到DAC，转换为一个模拟量  .

(4)和 进行比较。不相等的话接下来至此渐近寄存器的次高位变为1，最高位变为0.等等一系列变换，不断的去接近.直到等于 。

 

这里 就是我们想要转换的模拟信号（就是模数转换的目的就是想把他转换成数字量，换句话说我们在转换器中输入一个模拟量，经转换输出一个数字量，那么这个输入的模拟量就是）。

 

如果 = .那么。逐次渐近寄存器中的值就是 经过转换后得到的数字量，将这个数字量输出