数模-微分方程（概述、导弹引例问题、建立微分方程、MATLAB求微分方程解析解）

微分方程的框架

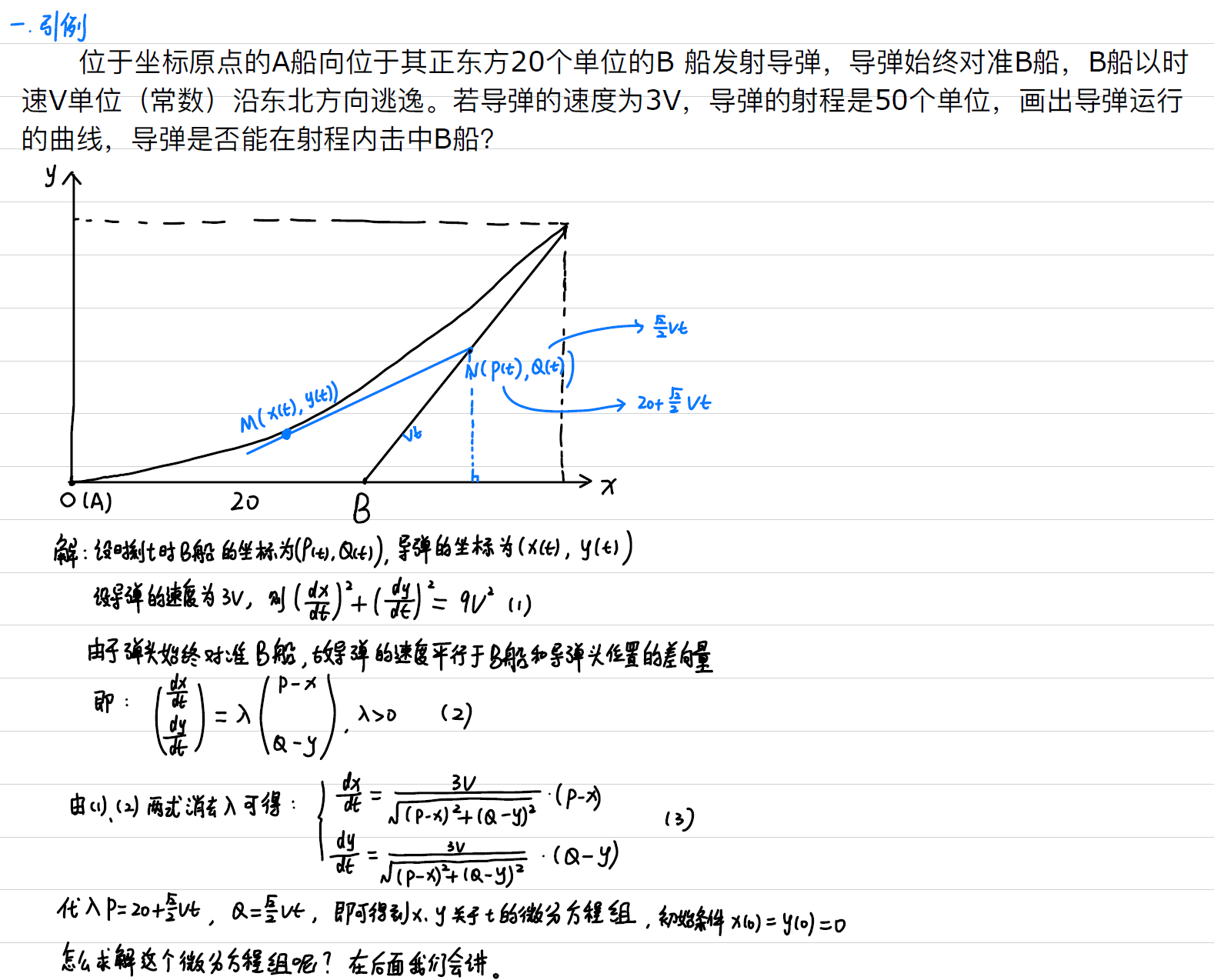
导弹引例问题

基本概念和怎样建立微分方程

MATLAB求微分方程解析解

%% 例1
clear;clc
dsolve('y-Dy=2*x','x')  % 这里要指定自变量为x
% 2*x + C1*exp(x) + 2  (这里的C1表示任意常数，有时候也会出现C2 C3等)
dsolve('y-Dy=2*x')  % 如果不指定自变量的话，会默认自变量为t，x会看成一个常数
% 2*x + C2*exp(t)

% 注意：最新版本的matlab会逐渐淘汰上面那种写法（虽然我个人觉得上面的写法更方便）
% 下面这种写法是新版的matlab推荐的方式（和我们上一讲符号运算中解方程的写法类似）
syms y(x)
eqn = (y - diff(y,x) == 2*x);    % 注意原来方程中的“=”一定要改成“==”
dsolve(eqn)

%% 如果微分方程中还有其他的未知参数怎么办？
% 方法1
dsolve('y-Dy=a*x','x')  % a是一个未知的参数
% 方法2
syms y(x) a
eqn = (y - diff(y,x) == a*x);  
dsolve(eqn)

%% 例2 
% 方法1
dsolve('y-Dy=2*x','y(0)=3','x')
% 2*x + exp(x) + 2
% 方法2
syms y(x)
eqn = (y - diff(y,x) == 2*x);  
cond = (y(0) == 3);
dsolve(eqn,cond)
% 2*x + exp(x) + 2


%% 例3
% 方法1
dsolve('D2y+4*Dy+29*y=0','y(0)=0,Dy(0)=15','x') 
% 3*sin(5*x)*exp(-2*x)
% 方法2
syms y(x)
eqn = (diff(y,x,2) + 4 *diff(y,x) + 29*y  == 0);  
Dy = diff(y,x); % 定义变量Dy为y的一阶导数
cond = [(y(0) == 0) ,(Dy(0) ==15)] ; % 有两个条件，可以写到一个向量中保存
dsolve(eqn,cond)
% 3*sin(5*x)*exp(-2*x)

%% 例4
% 方法1
[x,y,z] = dsolve('Dx=2*x-3*y+3*z+t','Dy=4*x-5*y+3*z+t','Dz=4*x-4*y+2*z+t','t') 

% 方法2
syms x(t) y(t) z(t)
eqn1 = (diff(x,t)  == 2*x-3*y+3*z+t); 
eqn2 = (diff(y,t)  == 4*x-5*y+3*z+t); 
eqn3 = (diff(z,t)  == 4*x-4*y+2*z+t); 
eqns = [eqn1 eqn2 eqn3];
[x,y,z] = dsolve(eqns)
% x = exp(2*t)*(C2- (exp(-2*t)*(2*t + 1))/4) + C3*exp(-t)
% y = exp(2*t)*(C2 - (exp(-2*t)*(2*t + 1))/4) + C3*exp(-t) + C4*exp(-2*t)
% z = exp(2*t)*(C2 - (exp(-2*t)*(2*t + 1))/4) + C4*exp(-2*t)
mupad  % 最新版本matlab可能会报错，将计算结果复制到里面，使结果可读。
% 如果新版matlab用不了mupad的话，可以使用更新13中介绍到的实时脚本
simplify(y)  % simplify函数可以简化表达式
latex(y) % 转换成latex代码，复制到Axmath或者word自带的公式编辑器（低版本不知道支不支持）
% 如果太过于复杂的话可能会报错，大家可以自己测试

%% 不是所有的微分方程都可以，导弹追击那一题就没有解析解
% 假设 v=100
[x,y] = dsolve('Dx = 3*100*(20+sqrt(2)/2*100*t-x)/sqrt((20+sqrt(2)/2*100*t-x)^2+(sqrt(2)/2*100*t-y)^2)','Dy = 3*100*(sqrt(2)/2*100*t-y)/sqrt((20+sqrt(2)/2*100*t-x)^2+(sqrt(2)/2*100*t-y)^2)','x(0)=0,y(0)=0','t')  
% 警告: Explicit solution could not be found.