雷达原理-目标距离测量
目标到雷达的距离 可以通过测量电波往返一次所需时间
得到:
时间 就是回波相对于发射信号的延迟,因此,目标距离测量就是要精确测量延迟时
。
根据雷达发射信号的不同,测定延迟时间通常可以采用:
- 脉冲法
- 频率法
- 相位法
一,脉冲法测距
1,基本原理
有两种定义回波到达时间 的方法:一种是以目标回波脉冲的前沿作为它的到达时刻;另一种是以回波脉冲的中心(或最大值) 作为它的到达时刻。
如果要测定目标回波的前沿,由于实际的回波信号不是矩形脉冲而近似为钟形,此时可将回波信号与一比较电平相比较,把回波信号穿越比较电平的时刻作为其前沿。用电压比较器是不难实现上述要求的。用脉冲前沿作为达时刻的缺点是容易受回波大小及噪声的影响。
后面讨论的自动距离跟踪系统通常采用回波脉冲中心作为到达时刻。回波脉冲中心估计如下图所示。
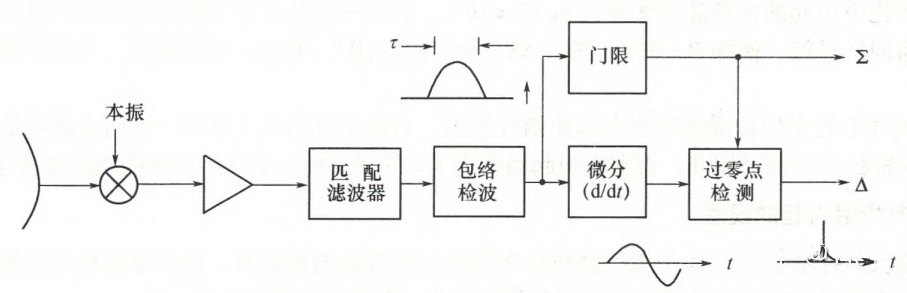
当微分器的输出经过零值时便产生一个窄脉冲,该脉冲出现的时间正好是回波视频脉冲的最大值,通常也是回波脉冲的中心。
2,影响测距精度的因素
根据公式:
可知, 和
、
有关。
分析精度通常使用高等数学里面的全微分的概念。对上式做全微分得:
用增量代替微分,可得到测距误差为:
其中, 为电波传播速度平均值的误差,
为测量目标回波迟延时间的误差。
(1)时间差的影响--------> \(dt_{R}\)越小,\(dR\)越小
(2)电波传播速度变化的影响--------->\(\frac{dR}{R}=\frac{dc}{c}\)
(3)大气折射的影响
(4)测读方法的影响
3,距离分辨率和测距范围
1)距离分辨力
距离分辨力(或距离分辨率)是指同一方向上两个大小相等点目标之间的最小可区分距离。用 表示。
:光电直径(单位:m)
:扫掠速度(单位:m/s)
\(d/v_{N}\):考虑光电的宽度之后得到的距离分辨率
我们希望距离分辨力 越小越好。根据上面的公式可知,这时对应的脉宽
就应该越小。
小之后会带来什么问题呢?
根据能量表示的雷达方程, ,如果
过小,信号能量就小,雷达最大作用距离就会下降。这就是说存在距离分辨力和最大作用距离的矛盾问题。
该怎么解决这个矛盾呢?
发射脉冲压缩波形,比如线性调频信号,接收时对回波进行匹配滤波。匹配滤波除了能提高信号的输出信噪比,还可以完成脉冲压缩的功能。这就可以解决距离分辨力和最大作用距离的矛盾问题。
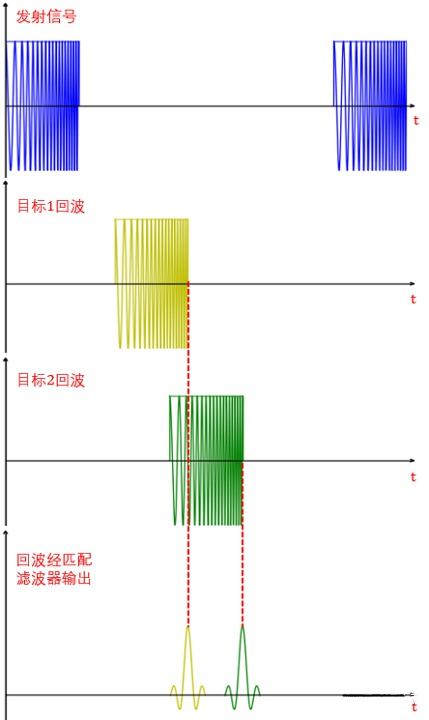
如果不做特殊处理,两个回波信号在时间轴上就叠加到了一起,无法区分开两个目标。如果将两个回波信号通过匹配滤波器,就可以得到如图所示的波形。匹配滤波器是一个线性系统,根据线性系统的叠加性,将两个回波信号叠加之后通过线性系统的输出,可以看成回波 1 通过线性系统的输出加上回波 2 通过线性系统的输出。
本来无法区分的两个目标,经过匹配滤波器之后变得可以区分,也就是说匹配滤波器有提高距离分辨力的作用。
那么提高之后的距离分辨力是多少呢?
这就跟图中两个辛克函数形状波形的宽度有关。如果这两个波形再靠近,直到相互交叠,目标也就无法区分开了。所以,距离分辨力也不说可以无限制的提升。
对于辛克函数,我们往往采用 -3dB 宽度来表示其宽度。但是,-3dB 的点往往不太规整,而 -4dB 的点反而比较规整,正好是 。所以,这里采用 -4dB 的点的宽度来表示辛克函数的宽度。
对于脉压雷达:
这里的 相当于前面的
。
为线性调频信号带宽。
线性调频信号:
对于频率:
线性调频信号带宽为:
对于普通雷达, 增大,
增大; 对于线性调频信号,
增大,
增大,
减小。
匹配滤波对于普通雷达而言,可以达到输出信噪比最大的作用。对于脉压雷达,可以提高距离分辨力。
关于 -3dB 的说明: 在角度、时间和频域三个维度都有 -3dB 的说法。-3dB 衡量的是最大值往下落 3dB 点位置之间的间隔。
a)如果间隔的单位为秒,就代表时间维度上的 -3dB,比如这一节中线性调频信号通过匹配滤波器之后的波形; b)如果间隔的单位为度,就代表角度维度上的 -3dB,主要用来衡量天线波束宽度; c)如果间隔的单位为赫兹,就代表频率维度上的 -3dB,比如门函数的频谱。
2)最大无模糊测距范围
测距范围包括最小可测距离和最大单值测距范围。所谓最小可测距离,是指雷达能测量的最近目标的距离。
收发共用天线的雷达系统中,在发射脉冲宽度 时间内,接收机和天线馈线系统间是“断开”的,不能正常接收目标回波,发射脉冲过去后天线收发开关恢复到接收状态,也需要一段时间
。也就是说在
这段时间内,由于不能正常接收回波信号,雷达是很难进行测距的。因此,雷达的最小可测距离为:
:收发转换时间。
雷达的最大无模糊距离由其脉冲重复周期 决定:
注意这里的 指最大无模糊距离。想要增大最大无模糊距离,可以增大
。
根据上一章的结论,积累脉冲数:
如果 增大,积累的回波数
就会减小。积累脉冲数减少,雷达探测距离就会下降(相参积累之后,最大作用距离变为
,这个
表示雷达最大作用距离)。这里就存在矛盾的地方。
雷达探测目标,首先应该考虑达到最大作用距离,这时 就确定下来了。再来考虑是否满足最大无模糊距离。如果不满足,就需要解模糊。
:目标到雷达的距离;
:假设跨了
个周期;
:回波离它最近主波之间的时间差。
3)距离模糊的判决方法
重频参差(两重频)如下图所示:
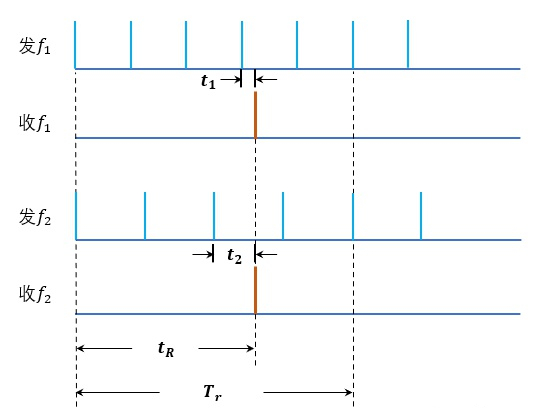
、
:对应两组发射脉冲的跨周期数。
一般取 ,上图中
。
和
可以看成是一个基础频率
上的一个倍频量。所以有:
根据公式:
当 时,
和
的关系可能有两种,即
和
。
假设 ,可得:
假设 ,可得:
如果按前式算出 为负值,则应采用后式。
重频参差的最大无模糊距离:
还有一个舍脉冲法,每发射M个脉冲,少发1个脉冲,那么接收回波也会在对应位置少一个脉冲,相当于用舍的脉冲做了一个标记,扩大了无模糊距离,扩大了M倍。
二、调频法测距
调频法测距可以用在连续波雷达中,也可以用于脉冲雷达。
调频连续波雷达的组成框图如下所示。发射机产生连续高频等幅波,其频率在时间上按三角形规律或按正弦规律变化,目标回波和发射机直接耦合过来的信号加到接收机混频器内。在无线电波传播到目标并返回天线的这段时间内,发射机频率较之回波频率己有了变化,因此在混频器输出端便出现了差频电压。后者经放大、限幅后加到频率计上。差频电压的频率实际上就与目标距离有关。
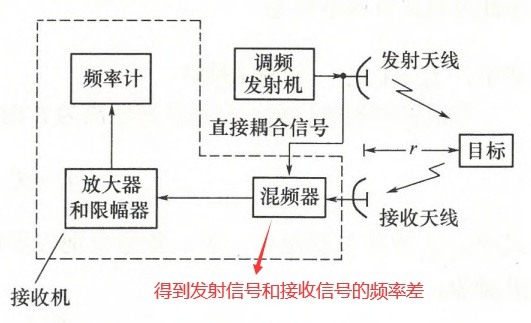
下面说明三角形波调制测距的数学原理。
发射频率按周期性三角波形的规律变化,如下图所示。
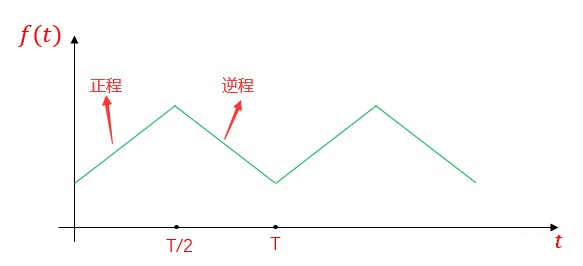
a)正程
发射频率:
对应发射信号的时域表示:
对应接收信号的时域表示:
:目标相对于雷达的径向速度,
:目标到雷达的初始距离。所以,接收信号的频率可以表示为:
:多普勒频率。由于
。
假设目标静止不动,即 ,上式可以写成:
从上式可以看出,接收信号的频率实际上就是将发射信号的频率迟延 。
b)逆程
发射频率:
接收频率:
发射信号和接收信号频率变化如下图所示。
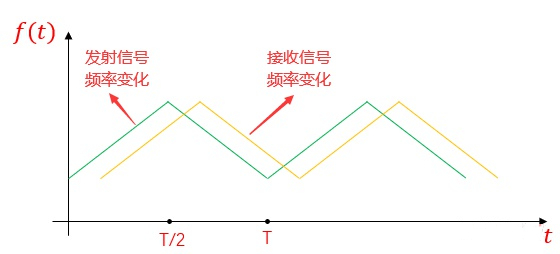
c)求差频的平均值
正程频率差,用 表示:
逆程频率差,用 表示:
频率计测得的差频的平均值,用 表示:
因此,可得:
频率计测频的一种方法
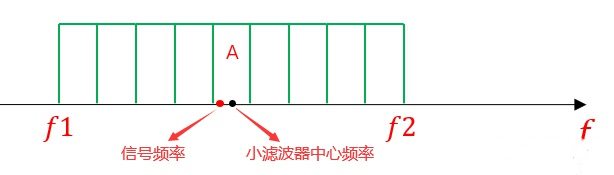
假设能够测频的范围为 。一种方法就是在这个范围内设计很多带宽相等的小滤波器,每个小滤波器都有一个中心频率。将差频得到的信号,送入如下的滤波器组。假设滤波器 A 有输出,其中心频率为图中黑点所示,真实信号频率为图中红点所示。我们就将滤波器 A 的中心频率作为该信号频率的测量值。如果滤波器带宽越窄,测频精度就越高。
三、距离跟踪的原理
测距时需要对目标距离进行连续的测量称为距离跟踪。
1、人工距离跟踪
主要采用的方法是锯齿电压波法和相位调制法。
2、自动距离跟踪
1)系统组成及功能
自动跟踪系统主要包括三部分:
时间鉴别器
时间鉴别器的作用是将跟踪脉冲与回波脉冲在时间上加以比较,鉴别出它们之间的差 。其数学模型为:
\(\Delta t\) 表示回波脉冲相对于基准发射脉冲的延迟时间。
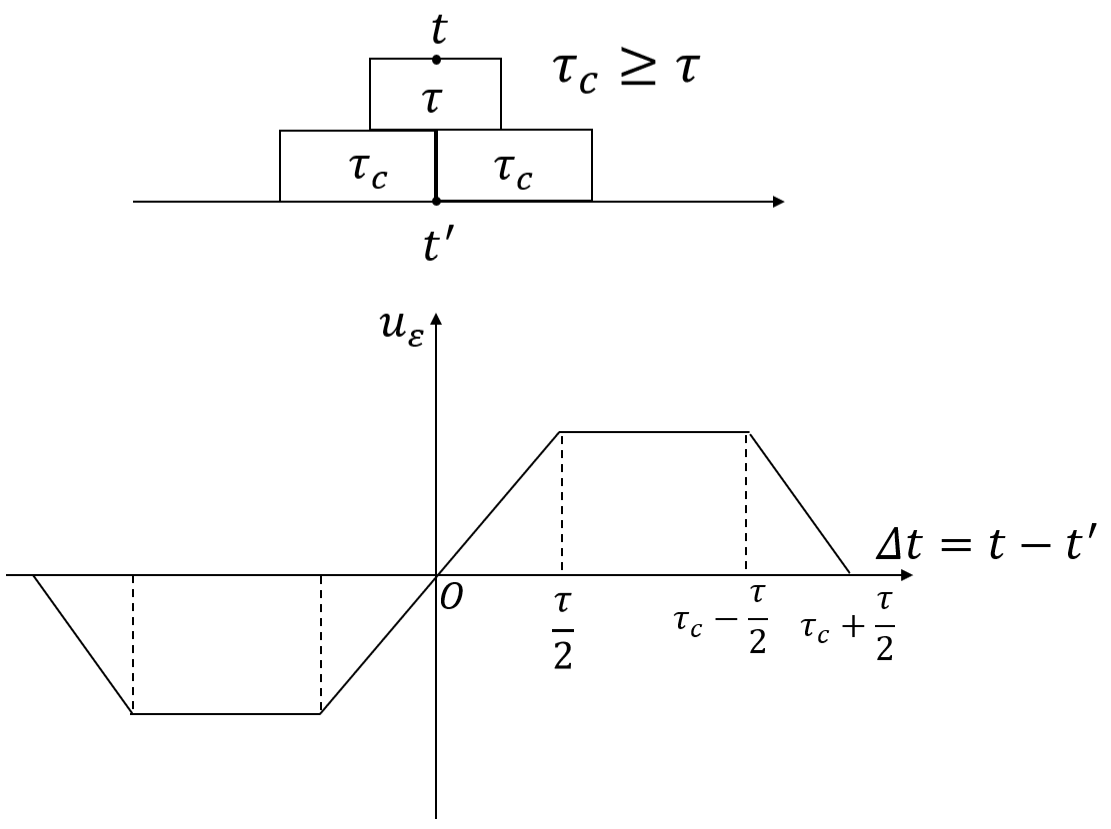
控制器的数学模型如下:
跟踪脉冲产生器的数学模型如下
上述过程是建立在 \(|\Delta t|\leq \tau_{c}+\frac{\tau}{2}\).
2)自动距离跟踪的步骤
- 搜索过程
- 跟踪过程
- 失锁,重新搜索


 浙公网安备 33010602011771号
浙公网安备 33010602011771号