20231408徐钰涵《密码系统设计》

20231408徐钰涵《密码系统设计》

第五周预习报告

学习内容

• 《Windows C/C++加密解密实战》第 7 章
• 课程 mindmap

AI对学习内容的总结

总结

• 数字签名的核心作用
  • 身份认证：确认信息发送者的身份。
  • 数据完整性：确保信息在传输过程中未被篡改。
  • 不可否认性：防止发送方事后否认其行为。
• 数字签名依赖的密码学基础
  • 基于非对称加密（公钥密码体制）。
  • 核心原理是私钥用于签名，公钥用于验证。
  • 常与Hash函数（如SHA1, SHA256）结合使用，先对长消息生成摘要，再对摘要签名，以提高效率。
• 数字签名必须满足的三个基本条件
  • 不可抵赖性：签名者事后无法否认自己的签名。
  • 不可伪造性：任何其他人都无法伪造签名者的签名。
  • 可仲裁性：发生争议时，第三方能够进行公正仲裁。
• 典型的数字签名算法分类（基于数学难题）
  • RSA：基于大整数素因子分解难题。
  • DSA/ElGamal：基于离散对数难题。
  • ECDSA：基于椭圆曲线离散对数难题。
• 几种特殊的数字签名及其用途
  • 盲签名：签名者不知道所签消息的具体内容，用于电子投票、电子现金系统。
  • 双重签名：将两条关联信息分别签名，保护隐私，用于安全电子交易（SET）协议。
  • 群签名：允许群体中的任一成员代表整个群体进行匿名签名。
  • 代理签名：可以将自己的签名权委托给代理者。
• RSA数字签名的具体过程
  • 签名：S = M^d mod n (使用发送方私钥)
  • 验证：M' = S^e mod n (使用发送方公钥)
  • 判断 M 是否等于 M'，相等则验证通过。
• 使用OpenSSL进行签名和验证的两种编程方式
  • 直接方式：使用 RSA_sign() 和 RSA_verify() 函数。
  • EVP高级方式：采用“初始化-更新-结束”三部曲，更推荐。
  • 签名：EVP_SignInit_ex -> EVP_SignUpdate -> EVP_SignFina
  • 验证：EVP_VerifyInit_ex -> EVP_VerifyUpdate -> EVP_VerifyFinal
• 数字签名的安全性研究主要方法
  • 安全性评估：设计者自行分析，评估方案强度。
  • 安全性证明：从理论上证明破解签名与解决一个公认数学难题同等困难。
  • 攻击分析：通过模拟攻击来发现并修复方案中的安全漏洞。
• 实际应用中的关键点
  • 为了保证安全，RSA密钥长度应足够长（如2048位以上）。
  • 应使用安全的Hash算法（如SHA256，避免使用MD5、SHA1）。
  • 数字签名是电子商务、网络安全协议、代码签名、法律文书等领域的基石技术。

对AI总结的反思与补充

反思与补充

问题

AI 总结中对签名与私钥加密的区别说的不是很清楚，容易让人误以为签名就是一种加密。

补充

• 严格来说，数字签名不是为了保密，而是为了证明身份和完整性。
• 如果对原文用私钥直接“加密”，虽然别人可以用公钥解开，但这不是标准的数字签名，因为：
  • 原文可能非常大，RSA效率极低
  • 缺乏结构化安全性，容易遭受构造攻击
  • 所以真实系统中采用：
    • Hash(消息) → 对 Hash 进行签名
  • 这使得：
    • 签名对象固定长度
    • 安全性取决于 Hash 的抗碰撞性
    • 更容易进行标准化验证

思维导图

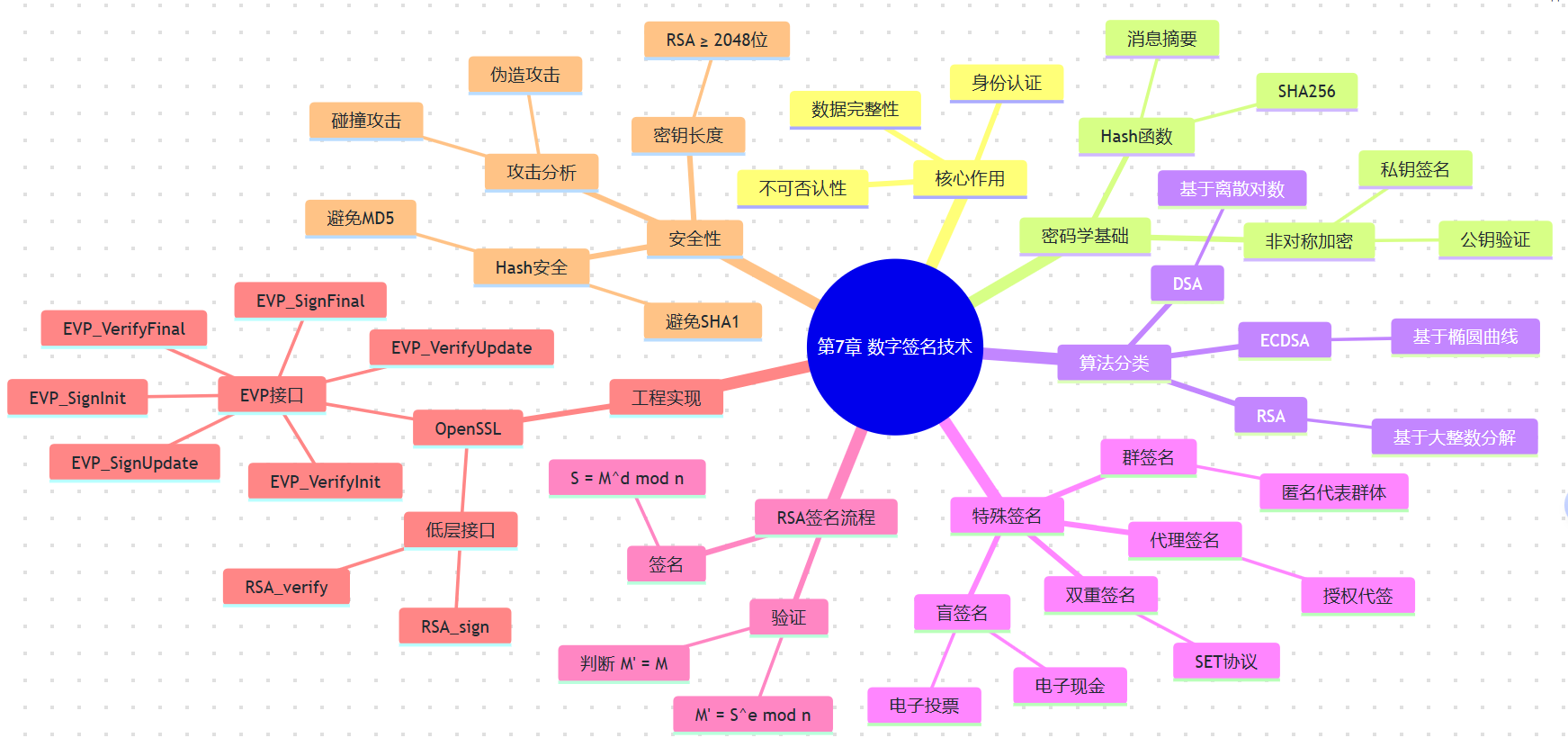
mindmap
  root((第7章 数字签名技术))
    核心作用
      身份认证
      数据完整性
      不可否认性
    密码学基础
      非对称加密
        私钥签名
        公钥验证
      Hash函数
        SHA256
        消息摘要
    算法分类
      RSA
        基于大整数分解
      DSA
        基于离散对数
      ECDSA
        基于椭圆曲线
    特殊签名
      盲签名
        电子投票
        电子现金
      双重签名
        SET协议
      群签名
        匿名代表群体
      代理签名
        授权代签
    RSA签名流程
      签名
        S = M^d mod n
      验证
        M' = S^e mod n
        判断 M' = M
    工程实现
      OpenSSL
        低层接口
          RSA_sign
          RSA_verify
        EVP接口
          EVP_SignInit
          EVP_SignUpdate
          EVP_SignFinal
          EVP_VerifyInit
          EVP_VerifyUpdate
          EVP_VerifyFinal
    安全性
      密钥长度
        RSA ≥ 2048位
      Hash安全
        避免MD5
        避免SHA1
      攻击分析
        伪造攻击
        碰撞攻击

基于AI的学习

学习内容

1. 数字签名的作用

我：我在学习数字签名，请你以苏格拉底式的方法向我提问，一次一个问题。

AI：数字签名中，谁掌握用来生成签名的密钥？

我：发送者。

AI：这个密钥是公开的还是私有的？

我：私有的。

AI：如果别人用你的公钥验证签名能通过，这说明签名是用谁的密钥生成的？

我：用我的私钥。

AI：而这个私钥只有谁有？

我：只有我。

AI：很好。这就说明只有你能生成这个签名，所以它证明了“是谁发的”，这就是身份认证。

2. 做RSA前先hash

我：我在学习RSA数字签名，请你以苏格拉底式的方法向我提问，一次一个问题。

AI：RSA签名的数学形式是 S = M^d mod N，对吗？

我：是。

AI：这里的 M 必须满足什么范围？

我：小于 N。

AI：如果原始消息是一个几百KB的文件，直接当成一个整数 M，有可能会发生什么？

我：会大于 N。

AI：如果 M ≥ N，RSA 取模会不会丢失信息？

我：会。

AI：那么解密时还能还原原始 M 吗？

我：不能。

AI：很好。所以如果不Hash，连“数学正确性”都不能保证，更不用谈安全性了。 

3. 直接签名原文会导致“可构造攻击”

我：我在学习RSA签名的安全性，请你以苏格拉底式的方法向我提问。

AI：RSA 的一个重要性质是乘法同态，对吗？也就是 (ab)^d ≡ a^d · b^d mod N。

我：是。

AI：如果攻击者看到两个签名 S1 = M1^d 和 S2 = M2^d，他能不能构造 S = S1·S2 mod N？

我：能。

AI：这个 S 在数学上等价于什么？

我：等于 (M1·M2)^d。

AI：也就是说，他伪造了哪个消息的签名？

我：M1×M2。

AI：很好。所以直接对原文签名，会导致“代数可伪造性”，这在密码学中是致命的。

学习实践过程遇到的问题与解决方式

1. 为什么不能把“加密”当作“签名”用？

• 问题：
  如果我用私钥去“加密”一段话，然后别人用公钥解密，这不就等于签名了吗？
• 解决：
  • 私钥加密 ≈ RSA签名
  • 公钥解密 ≈ 验签
  • 但真正的签名不是为了保密，而是为了：
    • 身份认证
    • 完整性
    • 不可抵赖
  • 如果直接对原文做私钥加密：
    • 数据很大 → 性能差
    • 结构可被攻击 → 不安全
    • 所以现实中采用：
      • Hash(消息) → 对 Hash 做签名

2. 为什么签名系统比加密系统更容易出错？

• 解决：
  • 在加密中，只要解密成功就算正确。
  • 但在签名中，攻击者的目标是：
    • 伪造一个“看起来合法的签名”
  • 这意味着：
    • 不能有数学结构漏洞
    • 不能有 Hash 碰撞
    • 不能有填充错误
  • 所以数字签名系统通常比加密系统更难设计，也更容易出严重漏洞

参考资料

• 《Windows C/C++加密解密实战》第 7 章
• 课程 MindMap
• AI 工具：ChatGPT