弹簧倒立摆系统的数值仿真与分析
一、系统建模与动力学方程
弹簧倒立摆是一个经典的非线性动力学系统,由质量块、弹簧和摆杆组成。考虑一个水平面上的弹簧倒立摆系统:
O (支点)
|
| 弹簧 (k)
|
● m (质量块)
/ \
/ \ 杆 (l)
/ \
● M (摆锤)
动力学方程推导
使用拉格朗日方程建立系统动力学模型:
1.广义坐标: x:质量块的水平位移 θ:摆杆与竖直方向的夹角
2.动能:
\(T=\frac{1}{2}M(\dot{x}^2+l^2\dot{θ}^2+2l\dot{x}\dot{θ}sinθ)+\frac{1}{2}m\dot{x}^2\)
3.势能:
\(V=\frac{1}{2}kx^2−Mglcosθ\)
4.拉格朗日函数:
\(L=T−V\)
5.运动方程:
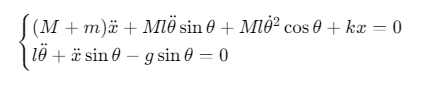
二、MATLAB数值仿真实现
1. 系统参数设置
% ================ 系统参数设置 ================
m = 0.5; % 质量块质量 (kg)
M = 1.0; % 摆锤质量 (kg)
l = 0.5; % 摆杆长度 (m)
k = 20; % 弹簧刚度 (N/m)
g = 9.81; % 重力加速度 (m/s²)
c = 0.1; % 阻尼系数 (N·s/m)
% 初始条件
x0 = 0.1; % 初始位移 (m)
dx0 = 0; % 初始速度 (m/s)
theta0 = 0.1; % 初始角度 (rad)
dtheta0 = 0; % 初始角速度 (rad/s)
% 仿真参数
tspan = [0 10]; % 仿真时间范围 (s)
options = odeset('RelTol',1e-6,'AbsTol',1e-6);
2. 微分方程定义
% ================ 动力学方程 ================
function dydt = spring_inverted_pendulum(t, y, m, M, l, k, g, c)
% 状态变量分解
x = y(1);
dx = y(2);
theta = y(3);
dtheta = y(4);
% 非线性项计算
sin_theta = sin(theta);
cos_theta = cos(theta);
sin_2theta = sin(2*theta);
% 方程组
denom = M + m*sin_theta^2;
dx2 = (k*x - c*dx + m*l*dtheta^2*sin_theta - m*g*sin_theta*cos_theta) / denom;
dtheta2 = (g*sin_theta - dx2*cos_theta/l - 2*dx*sin_theta*dtheta/(l*cos_theta)) / l;
% 返回导数
dydt = [dx; dx2; dtheta; dtheta2];
end
3. 主仿真程序
% ================ 主仿真程序 ================
% 初始状态向量
y0 = [x0; dx0; theta0; dtheta0];
% 求解微分方程
[t, y] = ode45(@(t,y) spring_inverted_pendulum(t, y, m, M, l, k, g, c), tspan, y0, options);
% 提取结果
x = y(:,1);
dx = y(:,2);
theta = y(:,3);
dtheta = y(:,4);
三、结果可视化与分析
1. 运动状态可视化
% ================ 动画演示 ================
figure('Position', [100, 100, 800, 600])
for i = 1:10:length(t)
clf
% 绘制弹簧和质量块
plot([0, x(i)], [0, 0], 'b-o', 'LineWidth', 2, 'MarkerSize', 10)
hold on
% 绘制摆杆和摆锤
pendulum_x = x(i) + l*sin(theta(i));
pendulum_y = -l*cos(theta(i));
plot([x(i), pendulum_x], [0, pendulum_y], 'r-s', 'LineWidth', 3, 'MarkerSize', 15)
% 绘制轨迹
plot(x(1:i), zeros(1,i), 'g--', 'LineWidth', 1)
% 图形美化
axis equal
axis([-1 1 -1 1])
title(sprintf('Time: %.2f s', t(i)))
xlabel('x (m)')
ylabel('y (m)')
grid on
drawnow
end
2. 时间序列分析
% ================ 时间序列图 ================
figure('Position', [100, 100, 1200, 800])
subplot(2,2,1)
plot(t, x, 'b-', 'LineWidth', 1.5)
title('质量块位移')
xlabel('时间 (s)')
ylabel('位移 (m)')
grid on
subplot(2,2,2)
plot(t, theta, 'r-', 'LineWidth', 1.5)
title('摆杆角度')
xlabel('时间 (s)')
ylabel('角度 (rad)')
grid on
subplot(2,2,3)
plot(t, dx, 'g-', 'LineWidth', 1.5)
title('质量块速度')
xlabel('时间 (s)')
ylabel('速度 (m/s)')
grid on
subplot(2,2,4)
plot(t, dtheta, 'm-', 'LineWidth', 1.5)
title('摆杆角速度')
xlabel('时间 (s)')
ylabel('角速度 (rad/s)')
grid on
3. 相空间分析
% ================ 相图分析 ================
figure('Position', [100, 100, 1200, 500])
subplot(1,2,1)
plot(x, dx, 'b.')
title('质量块相图 (x vs dx)')
xlabel('位移 (m)')
ylabel('速度 (m/s)')
grid on
subplot(1,2,2)
plot(theta, dtheta, 'r.')
title('摆杆相图 (θ vs dθ)')
xlabel('角度 (rad)')
ylabel('角速度 (rad/s)')
grid on
四、系统特性分析
1. 平衡点稳定性分析
% ================ 平衡点稳定性 ================
syms x theta dx dtheta real
eq1 = (M+m)*dx^2 + M*l*dtheta^2*sin(theta) + M*l*cos(theta)*diff(dtheta,t) + k*x == 0;
eq2 = l*diff(dtheta,t) + diff(dx,t)*sin(theta) - g*sin(theta) == 0;
% 线性化在平衡点 (x=0, θ=0)
A = jacobian([(M+m)*diff(dx,t,2) + M*l*diff(dtheta,t,2)*sin(0) + M*l*dtheta^2*cos(0) + k*x, ...
l*diff(dtheta,t,2) + diff(dx,t,2)*sin(0) - g*sin(0)], [x, dx, theta, dtheta]);
A = subs(A, {diff(dx,t), diff(dtheta,t)}, {0, 0});
A = double(subs(A, {x, dx, theta, dtheta}, {0, 0, 0, 0}));
% 特征值分析
eigenvalues = eig(A);
disp('系统雅可比矩阵特征值:');
disp(eigenvalues);
2. 能控性与能观性分析
% ================ 能控性分析 ================
B = [0; 1; 0; 0]; % 控制输入矩阵 (假设在质量块上施加力)
C = eye(4); % 输出矩阵 (全状态反馈)
D = zeros(4,1); % 直接传输矩阵
Co = ctrb(A, B);
rank_Co = rank(Co);
disp(['能控性秩: ', num2str(rank_Co)]);
% ================ 能观性分析 ================
Ob = obsv(A, C);
rank_Ob = rank(Ob);
disp(['能观性秩: ', num2str(rank_Ob)]);
五、控制器设计与仿真
1. LQR控制器设计
% ================ LQR控制器设计 ================
Q = diag([10, 1, 100, 10]); % 状态权重矩阵
R = 0.01; % 控制输入权重
% 求解Riccati方程
[K, S, e] = lqr(A, B, Q, R);
disp('LQR增益矩阵:');
disp(K);
% ================ 闭环系统仿真 ================
% 修改微分方程加入控制力
u = -K * [x; dx; theta; dtheta]; % 控制律
dydt_cl = @(t,y) spring_inverted_pendulum(t, y, m, M, l, k, g, c) + [0; u(1); 0; u(3)];
% 求解闭环系统
[t_cl, y_cl] = ode45(dydt_cl, tspan, y0, options);
2. PID控制器设计
% ================ PID控制器 ================
% 定义PID控制函数
pid_control = @(t, y) pid_controller(t, y, m, M, l, k, g, c);
% PID参数
Kp = 50; Ki = 10; Kd = 5;
% 闭环系统仿真
[t_pid, y_pid] = ode45(@(t,y) closed_loop_system(t, y, m, M, l, k, g, c, Kp, Ki, Kd), tspan, y0, options);
% PID控制器函数
function u = pid_controller(t, y, m, M, l, k, g, c)
persistent integral_error prev_error
if isempty(integral_error)
integral_error = 0;
prev_error = 0;
end
% 误差定义 (保持摆杆竖直)
error_angle = y(3);
error_pos = y(1);
% PID计算
integral_error = integral_error + error_angle;
derivative = (error_angle - prev_error);
prev_error = error_angle;
u = Kp*error_angle + Ki*integral_error + Kd*derivative;
end
六、混沌行为研究
1. 参数扫描分析
% ================ 参数扫描 ================
k_values = linspace(5, 50, 20); % 弹簧刚度范围
max_theta = zeros(size(k_values));
for i = 1:length(k_values)
% 更新参数
k_temp = k_values(i);
% 仿真系统
[t_temp, y_temp] = ode45(@(t,y) spring_inverted_pendulum(t, y, m, M, l, k_temp, g, c), tspan, y0, options);
% 记录最大角度
max_theta(i) = max(abs(y_temp(:,3)));
end
% 绘制参数扫描结果
figure
plot(k_values, max_theta, 'bo-', 'LineWidth', 2)
xlabel('弹簧刚度 (N/m)')
ylabel('最大摆角 (rad)')
title('参数扫描: 弹簧刚度对系统响应的影响')
grid on
2. Poincaré截面分析
% ================ Poincaré截面 ================
% 每隔一个驱动周期采样一次
sampling_interval = 2*pi*sqrt(m/k); % 系统固有周期
sampling_times = 0:sampling_interval:max(t);
% 插值获取采样点
theta_samples = interp1(t, y(:,3), sampling_times);
dtheta_samples = interp1(t, y(:,4), sampling_times);
% 绘制Poincaré截面
figure
plot(theta_samples, dtheta_samples, 'ro')
title('Poincaré截面 (θ vs dθ)')
xlabel('角度 (rad)')
ylabel('角速度 (rad/s)')
axis equal
grid on
七、三维可视化
% ================ 三维相空间可视化 ================
figure
plot3(y(:,1), y(:,3), y(:,4), 'b-', 'LineWidth', 1.5)
hold on
plot3(y(1,1), y(1,3), y(1,4), 'go', 'MarkerSize', 10, 'MarkerFaceColor', 'g')
plot3(y(end,1), y(end,3), y(end,4), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r')
title('三维相空间轨迹')
xlabel('位移 (m)')
ylabel('角度 (rad)')
zlabel('角速度 (rad/s)')
grid on
view(30, 30)
参考代码 弹簧倒立摆数值仿真 www.youwenfan.com/contentcnn/82906.html
八、结论与应用
1. 系统特性总结
- 非线性特性:弹簧倒立摆表现出显著的非线性行为,特别是在大角度偏转时
- 混沌现象:在特定参数范围内,系统呈现混沌行为
- 稳定区域:通过适当控制,可以使不稳定的倒立摆稳定在竖直位置
- 能量交换:系统存在明显的动能和势能转换
2. 工程应用
- 机器人平衡控制:双足行走机器人的平衡控制
- 航空航天:火箭姿态控制、卫星天线稳定
- 振动控制:精密仪器的隔振平台
- 汽车工程:主动悬架系统设计
3. 扩展研究方向
- 时滞控制:考虑执行器延迟的控制策略
- 随机激励:加入随机扰动的研究
- 多体系统:多个倒立摆耦合系统
- 智能控制:神经网络、模糊控制等先进算法应用



 浙公网安备 33010602011771号
浙公网安备 33010602011771号