软件构造学习（二）:AF和RI（表示不变性和抽象方程）

　　AF和RI，全称rep invariant和abstraction function，译为表示不变性和抽象函数。要想理解这两个的含义，必须先理解两个空间：一个是表示空间，简称R，包含的是抽象数据型的具体实现；另一个是抽象空间，简称A，是抽象值构成的空间，也就是客户看到和使用的值。两个空间之间的映射关系就可以理解为抽象函数，即如何去解释R中的每一个值为A中的每一个值。

• AF:R->A

　　AF可能有满射、未必单射、未必双射三种情况，但是尽量不要出现未必单射的情况，否则在判断对象是否相等时会很麻烦，因为判断对象是否相等是从客户的角度来说。下面是一个例子，在这当中就出现了未必单射的情况。这是因为表示不是一种严格的编码，有不止一种方法将无序字符表示成字符串。

 

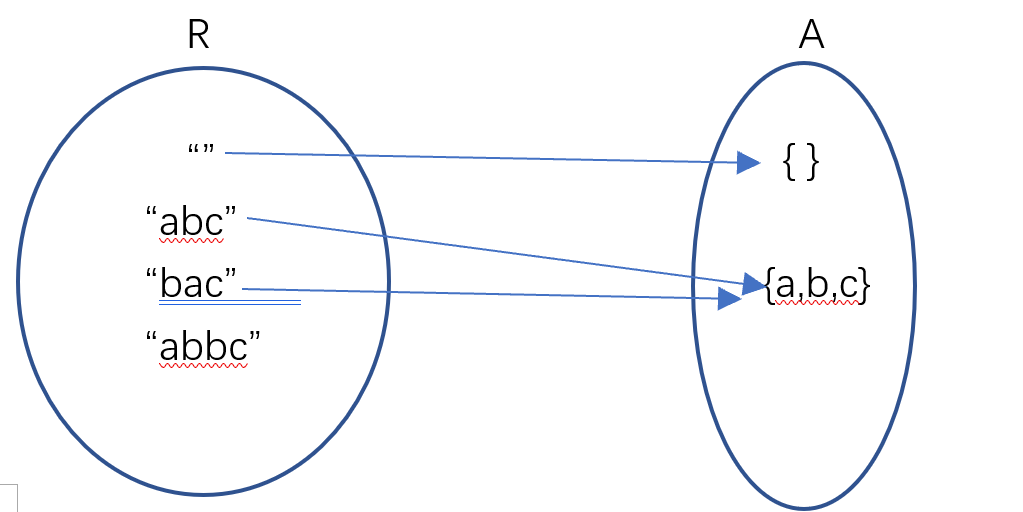
　　而表示不变性RI是指某个具体的“表示”是否是“合法”的，或者说是一种条件，描述了什么是“合法”的表示值。RI和AF都应该被记录在代码中。例如：

public class Charset{
    private s;
    //Rep invariant:
    // s contains no repeated characters
    //Abstaction function:
    //AF(s) = {s[i]|0<=i<s.length()}
    ...
}

　　在这里描述的“条件”就是不包含重复的字符，也就是此处的RI规定，只要不包含重复的字符，就都是“合法的”表示值。从s中取出所有的字符，构成集合，就是客户所需要的抽象值。也就是说设计一个ADT的过程就是：选择某种特定的表示方式R，进而指定某个子集是“合法的”（RI），并未该子集中的每个值做出“解释”（AF）——即如何映射到抽象空间中的值。当然，同样的R，同样的RI，也可能有不同的AF，也就是“解释”不同。这当中可以让用户看到的只有AF和A，这是因为具体的RI或者R要和具体的方法绑定，所以不能暴露给用户。

 　　checkRep（）函数，用来随时检查RI是否被满足，在所有有可能改变rep的方法内都要检查，从而使错误可以尽快地被检测到。所以对于构造器、生产器和变值器的方法内部都要用到checkRep（），而观察器不是必须使用，但是也要尽可能检查，以防止万一。