[Optimization] Greedy method

 “贪心算法” 算是 "动态规划" 的前置课程。

在数据结构graph中的优化问题也大量涉及到了”Greedy Method"。

也有五大常用算法之说：算法设计之五大常用算法设计方法总结

一、【分治法】

二、【动态规划法】

三、【贪心算法】

四、【回溯法】

五、【分支限界法】

 

 

贪心地关注边界

Given two sequences of letters A and B, find if B is a subsequence of A in the
sense that one can delete some letters from A and obtain the sequence B.

Greedy领先的思想。(always stay ahead)

Ref: https://www.geeksforgeeks.org/given-two-strings-find-first-string-subsequence-second/

A上的指针找B的头char，只要一样，就开始“齐头并进”对比。

如果出现不一样，就只移动A上的指针；毕竟，只要对比过的，对之后的也是有意义的。

 

 

覆盖的“范围”

避开最大"无效区"

There is a line of 111 stalls, some of which need to be covered with boards.
You can use up to 11 boards, each of which may cover any number of
consecutive stalls.

Cover all the necessary stalls, while covering as few total stalls as possible

一块大板，不断去掉大空隙。直到大板被分为要求的11个。

本质：排序“间隙”，先 eliminate 最大的间隙（贪心的体现）

Ref: https://projectalgorithm.wordpress.com/2011/04/25/greedier-than-you/

  

区间“完全覆盖”问题

给定一个长度为m的区间，再给出n条线段的起点和终点（注意这里是闭区间），

求最少使用多少条线段可以将整个区间完全覆盖。

区间长度8，可选的覆盖线段[2,6],[1,4],[3,6],[3,7],[6,8],[2,4],[3,5]

区间覆盖问题  《区间完全覆盖》

先按照“起始点”排序，结果如下：

Prove:

需要最少的线段进行覆盖，那么选取的线段必然要尽量长，而已经覆盖到的区域之前的地方已经无所谓了。

贪心策略就是：head是上一个tail之前的的情况下，看谁的len更长。

 

最大“不相交覆盖”

给定一个长度为m的区间，再给出n条线段的起点和终点（开区间和闭区间处理的方法是不同，这里以开区间为例），

问题是从中选取尽量多的线段，使得每个线段都是独立的，就是不和其它有任何线段有相交的地方。

例如：

区间长度8，可选的覆盖线段[2,6],[1,4],[3,6],[3,7],[6,8],[2,4],[3,5]，选的不能相交哦！

Ref: https://blog.csdn.net/chenguolinblog/article/details/7882316 

对线段的左端点进行升序排序，每加入一个线段，然后选择后面若干个（也有可能是一个）右端点相同的线段，选择左端点最大的那一条，如果加入以后不会跟之前的线段产生公共部分，那么就加入，否则就继续判断后面的线段

• 排序:

将每一个区间按右端点进行递增顺序排列，拍完序后为[1,4]，[2,4]，[2,6]，[3,5]，[3,6]，[3,7]，[6,8]

• 操作：

第一步选取[2,4]，发现后面只能加入[6,8],所以区间的个数为2

• 贪心证明:

因为需要尽量多的独立的线段，所以每个线段都尽可能的小！

对于同一右端点，左端点越大，线段长度越小。

 

区间选点问题 

用最少的钉子穿插所有的木条。

Greedy的对象的选择问题：

• • 穿插最多的优先 (greedy 失败)
  • 最早结束的优先 (greedy 成功) ----> 最早结束的“穿插的概率低”；晚结束的，可以放心一些。这体现了“贪心”。

 

 

覆盖的“个数”，而非“范围”

—— 给后者更多活路

 Find a maximum size subset of compatible activities.

求“一段时间内”能容纳的“最多活动数”。《最大不相交覆盖》

最早结束时间的活动优先，保最多的空余时间，才可能会有更多的“活动数”，体现“贪心”。

Transforming any optimal solution to the greedy solution with equal number of
activities

find that proving the greedy solution is also optimal.

证明：

greedy exchange, 即证明greedy所得结论不会worse.

Extended: 

“最多活动数” ==> "总的最长活动时间“，且”每个活动时间不等“，则，greedy失效，需dynamic programming.

 

 

There are N robbers who have stolen N items. You would like to distribute the items
amongst the robbers (one item per robber). You know the precise value of each item.
Each robber has a particular range of values they want their item to be worth

(too cheap and they will not have made money, too expensive and they will draw a lot of attention).

Devise an algorithm that can distribute the items so each robber is happy or determines that there is no such distribution.

From: 从零开始学贪心算法

“最大活动数”的变形题。

如果我们每次都选择开始时间最早的活动，不能得到最优解：

 

如果我们每次都选择持续时间最短的活动，不能得到最优解：

 

(贪心体现)

可以用数学归纳法证明，我们的贪心策略应该是每次选取结束时间最早的活动。

直观上也很好理解，按这种方法选择相容活动为未安排活动留下尽可能多的时间。这也是把各项活动按照结束时间单调递增排序的原因。

Sol:

对物品价值v升序排序。遍历每一个物品价值 v：

最小bound在范围内，即当前v的左边，最大bound也在（这是默认肯定的），这些 j 构成一个集合。

分配集合中“最大bound”最小的那个 to robber。　　

例如分配v3时的 j3, j4：j4的tail大，所以把机会留给j3。

隐含的道理是：

• • 只关心tail，不关心head。因为head在此不管有多早似乎都对以后的分配都没有意义。
  • 思考：j1与j2可以互换么？

Prove：

“Cut-and-paste" arguments.

改变一个逆序，不会变得更糟。因为，减少一个逆序，例如 j2重新在j1之前，那么j2的deadline更久，就更能成立！

 

 

Schedule all the jobs so that the lateness of the job with the largest lateness is minimised.

最小化任务延迟

只关心deadlines，体现了贪心。

证明：（交换论证）

关键步骤的证明是"减少一个逆序de调度导致的最大延迟不会更糟". 

 

 

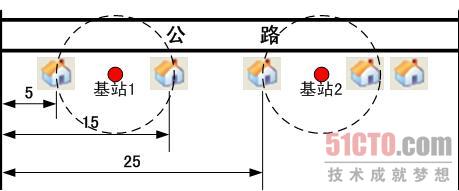
Along the long, straight road from Loololong to Goolagong houses are
scattered quite sparsely, sometimes with long gaps between two
consecutive houses. Telstra must provide mobile phone service to people
who live alongside the road, and the range of Telstras cell base station is
5km.

Design an algorithm for placing the minimal number of base stations alongside the road, that is sufficient to cover all houses.

一个思考：从左到右，从右到左，既然都是greedy，minimum是一样的，但stations的位置却不同。

有点类似之前board覆盖stall的习题，也类似“插棍子”。从左往右时，关注覆盖左边的边缘，体现“贪心”。

 

 

 

“先处理”的隐藏累赘代价

Assume you are given n sorted arrays of different sizes. You are allowed
to merge any two arrays into a single new sorted array and proceed in
this manner until only one array is left.

Design an algorithm that achieves this task and uses minimal total number of moves of elements of
the arrays. Give an informal justification why your algorithm is optimal.

类似Merge sort过程的，huffman code原理的东东。

较小的块优先合并。(合并时有排序过程)

合并后的较大的块，如果还有后续的操作，那么前面合并得越大，将会成为后续移动操作中的累赘。

 

 

贪心“重要性密度”

A list of n files fi of lengths li which have to be stored on a tape.
Each file is equally likely to be needed. To retrieve a file, one must start from
the beginning of the tape and scan it until the tape is found and read.

Order the files on the tape so that the average (expected) retrieval time
is minimised.

如果p不再均匀，则比较P/L，证明如下。

把长度最小的放前面，平均读取时间最小；这体现了贪心。

如果非均匀，则“假设swap其中的两个”，再比较E。（具体见上图公式）

 

 

只有一台机器，单线程执行某个人交代的的任务，任务的重要性不同。

最小化 总的“重要性*截止时间”

贪心比较"重要性密度"：Schedule jobs in decreasing order of the ratio ri = wi /ti  （重要性/任务时长）

prove:

假设有更好的方案。而后减少逆序看变化。

类似 the tape storage problem。

 

 

最小生成树 a minimum spanning tree 

You are given a connected graph with weighted edges. Find a spanning tree

such that the largest weight of all of its edges is as small as possible.

求加强连通图的最小生成树

为何最优？

• • Kruskal Algo: sort e by cost 以edge为主角，则适合"稀疏图"
  • Prim Algo: start from any vertex, add lightest edge one by one. 以vertex为主角，则适合"稠密图"

Ref: 最小生成树-Prim算法和Kruskal算法

Ref: https://blog.csdn.net/a2392008643/article/details/81781766

Goto: [Algorithm] Graph

 

 

Design an algorithm which produces a minimum spanning tree T 0 for the

new graph containing the additional vertex vn+1 and which runs in time O(n log n).

New vertex与其他n个vertex的edge 做排序，选最小的，体现了“贪心”。

 

 

There are n radio towers for broadcasting tsunami warnings. You are given the coordinates of each tower and its radius of range.

When a tower is activated, all towers within the radius of range of the tower will also activate, and those can cause other towers to activate and so on.

You need to equip some of these towers with seismic sensors so that when these sensors activate the towers where these sensors are located all

towers will eventually get activated and send a tsunami warning.

The goal is to design an algorithm which finds the fewest number of towers you must equip with seismic sensors.

总有一个塔，在连锁反应中能激活最多的其他塔。给它安装报警器即可。

 

 

Partition the vertices of G into k disjoint subsets so that the minimal distance between two points belonging to different sets of the partition is as large as possible.

Thus, we want a partition into k disjoint sets which are as far apart as possible.

Sort the edges in increasing order and start performing the usual
Kruskal’s algorithm for building a minimal spanning tree,

but stop when you obtain k trees, rather than a single spanning tree.

最小生成树的生成过程中，红线肯定大于任何一条蓝线，体现了“贪心”。

时间复杂度：

N = n^2条边，O(N * N log N).

采用“并查集”数据结构后，

we make at most 2n2 calls of the Find operation and at most n calls of the Union operation.

 

 

Assume that a weighted (undirected) graph G = (V, E) has all weights of edges
distinct and that its set of vertices V has been partitioned into two disjoint subsets,
X and V \X and assume that an edge e = (u, v) is the smallest weight edge whose
one end belongs to X and the other end to V\X (Y). Prove that every spanning tree
must contain edge e.

证明过程：(假设法)

经过e，那么e把图分为了两份。

你丫说不经过e，那么就是经过其他边儿咯？加上你说的这条边，但暂时不删除e，是不是就构成了一个circle？

circle里，谁最小？！当然e最小！

有最小的e，为何还要你说的那条边？！故，你的逻辑有矛盾，得证。

 

Extended:

Let G = (V, E) be a weighted (undirected) graph has all weights
of edges distinct and let e be the highest weight edge in C.

Prove that e cannot belong to the minimum spanning tree.

证明 circle 里的最大边，不可能属于MST（最小生成树）

反证法：

如果是的话，这条边把图一分为二，再加个其他边，假设为其他方案中选中了这条，而不是这个最大边e，

那么，又出现了一个circle。

可见，还不如不要最大边e为好。

 

Extended:

Assume that you are given a weighted (undirected) graph G = (V, E) with all weights of edges distinct and its minimum spanning tree T.

Assume now that you add a new edge e to G. Design a linear time algorithm which produces the minimum spanning tree for the new graph with the additional edge.

在已有的MST中加了新边e，如何更新MST（最小生成树） 

Sol:

(1) 加了新边后会出现一个新circle，

(2) 然后删掉环上的最大边。

 

 

拟阵理论 - matroid

Scheduling unit jobs with penalties and deadlines.

The problem of scheduling unit-time tasks with deadlines and penalties for a single processor has the following inputs:

 a set S = {1, 2, . . . , n} of n unit-time tasks;

 a set of n integer deadlines d₁, d₂, . . . , d_n, such that each d_i satisfies 1  d_i  n and task i is supposed to finish by time d_i; and

 a set of n nonnegative weights or penalties w₁,w₂, . . . , w_n, such that a penalty w_i is incurred if task i is not finished by time d_i and no penalty is incurred if a task finishes by its deadline.

We are asked to find a schedule for S that minimizes the total penalty incurred for missed deadlines.

Ref: 一个任务调度问题-----算法导论

Theory:

实现任务的最优调度主要就是利用贪心算法中拟阵的思想。

如果S是一个带期限的单位时间任务的集合，且I是所有独立的任务集构成的集合，则对应的系统 M =（S，I）是一个拟阵。满足如下条件:

1. 1. S是一个非空有穷集合； 
   2. l⊆2^S且ϕ∈l (I为S的非空子集族)
   3. l满足交换性质 (Augmentation)：若A∈l,B∈l且|A|<|B|，则∃x∈B−A，使得A∪{x}∈l （这条性质给了我们已知集合B，构造集合A的方法）
   4. l满足遗传性质 (Downward closure)：若B∈l,A⊆B，则A∈l. Or, B是S的独立子集，这样B的任意子集也都是S的独立子集。（暗示了我们已知集合B，找出其子集的性质的办法）

 

利用拟阵解决任务调度问题的算法原理主要就是：

将最小化迟任务的惩罚之和问题 ----> 转化为 ----> 最大化早任务的惩罚之和的问题，

也就是说在任务调度的时候 优先选择当前任务序列中惩罚最大的任务（体现了"贪心"）。

这里，假设集合A存放任务的一个调度。如果存在关于A中任务的一个调度，使得没有一个任务是迟的，称任务集合A是独立的。

Prove:

(1) 先证明其是拟阵

(2) 可采用最大化早任务的惩罚和的"贪心"算法。

Extended:

O(n)次独立性检查的每一次都用O(n)时间。如何优化？

并查集。

 

实验操作

n取值为7，每个任务的期限为4, 2, 4, 3, 1, 4, 6，对应的惩罚为70, 60, 50, 40, 30, 20, 10。

放弃了a5, a6。

 

 

"贪心法”的适用特点

Assume you have $2, $1, 50c, 20c, 10c and 5c coins to pay for your lunch.

Design an algorithm that, given the amount that is a multiple of 5c, pays it with a minimal number of coins.

明显是从大面值开始。类似于人民币问题，找零时符合贪心算法。

Prove:

满足“最优子结构性质”，“贪心选择性质”。link

最优子结构性质

　　一个问题的最优解包含其子问题的最优解。（子结构也是子问题的最优解）

• 设立一个事实：

例如95c = 50c + 20c + 20c + 5c 这个贪心算法的结果是最优解，是满足optimal substrcuture的。

• 做一个推断：

少一个20c，本应该推断是75c的最优解；

• 韭菜突然假设：

75c可鞥有更好的解？“两张纸币就能搞定“。

• 与”原事实“的冲突：

那么在你这个假设的基础上可以认为 加一个20c成为了“仅需3张纸币就能达到95c的最优解“，这与原事实冲突！

故，贪心算法所得结果是满足“最优子结构性质”。

 

贪心选择性质

整体最优解，可以通过一系列局部最优的选择来达到。（每张纸币的量已是最优，不可能更大）

• 设立一个事实：

贪心算法的结果应保证了“每个面额不可能更多，即已是最大”。因为贪心嘛。

• 韭菜突然假设：

因为，总额不变，纸币量减少的话：减少任意的相对小的纸币（这导致需要更大的面额的纸币来填充差额）

• 与“原事实”的冲突：

贪心解已满足每张纸币面额达到了最大 (贪心的本质)，故产生矛盾。

故，原问题满足“贪心选择性质“。

 

贪心失效

贪心算法（按单位重量价值排序）（含为什么不可以解决） goto: 0-1背包问题、贪心算法、动态规划

• • 找换硬币问题 与 0-1背包问题区别【贪心适用、动态规划适用的分析】
  • 对于有些情况下，贪心算法失效！比如硬币面值1,10,25。找30分钱，最优解是3*10，而贪心的情况下产生的解是1*5+25。
  • 指数增长的面额情况时，可换的硬币的单位（或者称 面值）是 c 的幂，也就是 c⁰，c¹，... ，c^k，其中整数 c>1，k>=1。

Prove:

常识一：

对于最优解而言，如果使用了面值为 cⁱ 的硬币去找零，那么 cⁱ 最多只能使用 c-1 个。若使用c个的话，c*cⁱ 意味着可以使用一张更大面额纸币来替换众多小纸币。

根据常识一，

如果非贪心是最优的，非贪心使用的所有面值为c^i的硬币个数应该小于c。否则，不是最优！

 

 

具有"动态限制"的贪心 

Suppose you have n video streams that need to be sent, one after another, over a communication link.

Stream i consists of a total of bi bits that need to be sent, at a constant rate, over a period of ti seconds.

You cannot send two streams at the same time, so you need to determine a schedule for the streams:

an order in which to send them. Whichever order you choose,

there cannot be any delays between the end of one stream and the start of the next.

Suppose your schedule starts at time 0. We assume that all the
values bi and ti are positive integers. Now, because you're just one user, the link does
not want you taking up too much bandwidth, so it imposes the following constraint,
using a fixed parameter r:

For each natural number t > 0, the total number of bits you send over the time interval from 0 to t cannot exceed rt.

Note that this constraint is only imposed for time intervals that start at 0, not for
time intervals that start at any other value. We say that a schedule is valid if it
satisfies the constraint.

Example.

Suppose we have n = 3 streams, with (b1, t1) = (2000, 1), (b2, t2) = (6000, 2), (b3, t3) = (2000, 1), and suppose the link’s parameter is r = 5000.

Then the schedule that runs the streams in the order 1, 2, 3, is valid, since the constraint (*) is satisfied:

• t = 1: the whole first stream has been sent, and 2000 < 5000 · 1
• t = 2 : half the second stream has also been sent, and 2000 + 3000 < 5000 · 2.

Similar calculations hold for t = 3 and t = 4.

link

不同的stream，单位时间能发送的bit不同。（理解为压缩的效率不同即可）

右侧的 rt 代表了一种动态的limitation，理解为：带宽限制。

这里只是判断下：是否存在 满足如此条件的schedule。

贪心自然是：

能尽可能地 reach/follow this limitation as far as possible。

找最可能的方式，即是保持limitation的距离越远越好。

 

Design:

(a) In O(nlogn), order the streams in increasing order of bi/ti (压缩率) , and check if this schedule has the desired property.

(b) To get an ordering in O(n) time define si = r*ti − bi and schedule streams so that you
start with all streams for which si is non-negative, in any order, followed by those for which si is negative, also in any order.

(因为只要把小于r*ti的排在前面，大于的排在后面即可，至于排序操作，确实是多余)

Prove:

交换论证（exchange argument）

 

End.