[Scikit-learn] Dynamic Bayesian Network - HMM
Warning The sklearn.hmm module has now been deprecated due to it no longer matching the scope and the API of the project. It is scheduled for removal in the 0.17 release of the project.
From: http://scikit-learn.sourceforge.net/stable/modules/hmm.html
The sklearn.hmm module has now been deprecated due to it no longer matching the scope and the API of the project. It is scheduled for removal in the 0.17 release of the project.
hmmlean
This module has been moved to a seperate repository: https://github.com/hmmlearn/hmmlearn
hmmlearn doc: http://hmmlearn.readthedocs.io/en/latest/
其他参考链接:
HMM的Baum-Welch算法和Viterbi算法公式推导细节
涉及的三个问题都是什么,以及解决每个问题的主流算法:
- 概率计算问题即模型评价问题——前向算法和后向算法
- 学习问题即参数估计问题——Baum-Welch算法
- 预测问题即解码问题——Viterbi算法
Ref:https://www.zhihu.com/question/20962240/answer/33438846
掷骰子
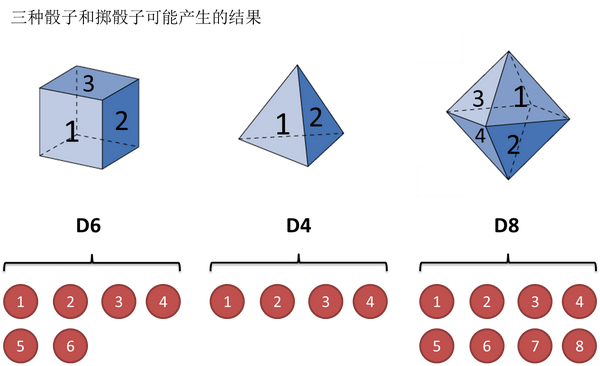
可见/隐含状态链
这串数字叫做可见状态链。
转换概率/输出概率
同样的,尽管可见状态之间没有转换概率,
提出问题
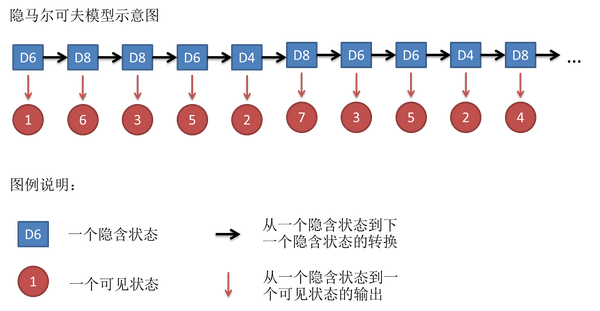
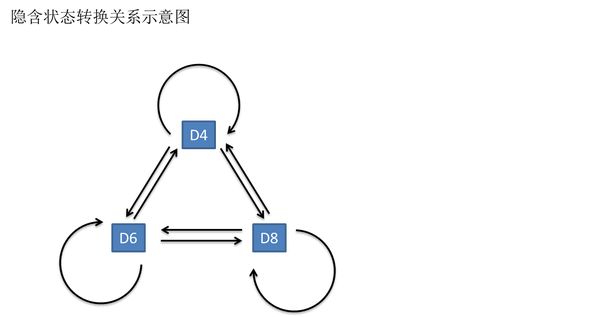
其实对于HMM来说,如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率,做模拟是相当容易的。
-
- 有时候你知道骰子有几种,每种骰子是什么,但是不知道掷出来的骰子序列;
- 有时候你只是看到了很多次掷骰子的结果,剩下的什么都不知道。
回到正题,和HMM模型相关的算法主要分为三类,分别解决三种问题:
1)知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道每次掷出来的都是哪种骰子(隐含状态链)。
这个问题呢,在语音识别领域呢,叫做解码问题。
- 第一种解法求最大似然状态路径,说通俗点呢,就是我求一串骰子序列,这串骰子序列产生观测结果的概率最大。(这里只讲这个)
- 第二种解法呢,就不是求一组骰子序列了,而是求每次掷出的骰子分别是某种骰子的概率。比如说我看到结果后,我可以求得第一次掷骰子是D4的概率是0.5,D6的概率是0.3,D8的概率是0.2。
2)还是知道骰子有几种(隐含状态数量),每种骰子是什么(转换概率),根据掷骰子掷出的结果(可见状态链),我想知道掷出这个结果的概率。
看似这个问题意义不大,因为你掷出来的结果很多时候都对应了一个比较大的概率。问这个问题的目的呢,其实是检测观察到的结果和已知的模型是否吻合。
3)知道骰子有几种(隐含状态数量),不知道每种骰子是什么(转换概率),观测到很多次掷骰子的结果(可见状态链),我想反推出每种骰子是什么(转换概率)。
这个问题很重要,因为这是最常见的情况。很多时候我们只有可见结果,不知道HMM模型里的参数,我们需要从可见结果估计出这些参数,这是建模的一个必要步骤。
0. 一个简单问题
“知道骰子有几种,每种骰子是什么,每次掷的都是什么骰子,根据掷骰子掷出的结果,求产生这个结果的概率。”
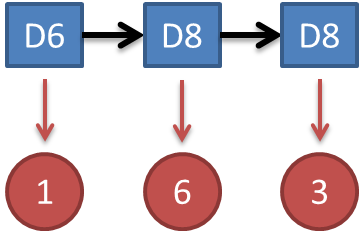
1. 看见不可见的,破解骰子序列
其实最简单而暴力的方法就是穷举所有可能的骰子序列,然后依照第零个问题的解法把每个序列对应的概率算出来。然后我们从里面把对应最大概率的序列挑出来就行了。如果马尔可夫链不长,当然可行。如果长的话,穷举的数量太大,就很难完成了。
另外一种很有名的算法叫做Viterbi algorithm. 要理解这个算法,我们先看几个简单的列子。
(1)首先,如果我们只掷一次骰子:

因为D4产生1的概率是1/4,高于1/6和1/8,so,对应的最大概率骰子序列就是D4,
(2)把这个情况拓展,我们掷两次骰子:

结果为1,6.这时问题变得复杂起来,我们要计算三个值,分别是第二个骰子是D6,D4,D8的最大概率。

写到这里,大家应该看出点规律了。既然掷骰子一二三次可以算,掷多少次都可以以此类推。我们发现,我们要求最大概率骰子序列时要做这么几件事情。首先,不管序列多长,要从序列长度为1算起,算序列长度为1时取到每个骰子的最大概率。然后,逐渐增加长度,每增加一次长度,重新算一遍在这个长度下最后一个位置取到每个骰子的最大概率。因为上一个长度下的取到每个骰子的最大概率都算过了,重新计算的话其实不难。当我们算到最后一位时,就知道最后一位是哪个骰子的概率最大了。然后,我们要把对应这个最大概率的序列从后往前推出来。
2. 谁动了我的骰子?
比如说你怀疑自己的六面骰被赌场动过手脚了,有可能被换成另一种六面骰:【异常色子的信息也已知】
- 算一算正常的三个骰子掷出一段序列的概率,
- 再算一算不正常的六面骰和另外两个正常骰子掷出这段序列的概率。
比如说掷骰子的结果是:

我们会应用一个和前一个问题类似的解法,只不过前一个问题关心的是概率最大值,这个问题关心的是概率之和。解决这个问题的算法叫做前向算法(forward algorithm)。
首先,如果我们只掷一次骰子:

看到结果为1。产生这个结果的总概率可以按照如下计算,总概率为0.18:

把这个情况拓展,我们掷两次骰子:

看到结果为1,6.产生这个结果的总概率可以按照如下计算,总概率为0.05:

继续拓展,我们掷三次骰子:

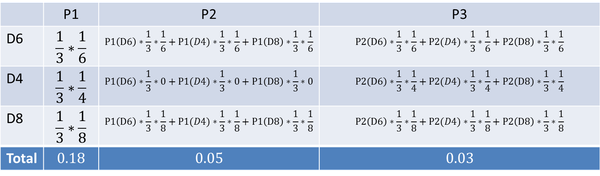
同样的,我们一步一步的算,有多长算多长,再长的马尔可夫链总能算出来的。
以上是一些基础问题。
模型这东西,不结合实际features搞一搞,不利于深入理解。
HMM的理解 in NLP
From: https://zhuanlan.zhihu.com/p/26811689
应用到词性标注中,v代表词语,是可以观察到的。q代表我们要预测的词性(一个词可能对应多个词性)是隐含状态。
应用到分词中,v代表词语,是可以观察的。q代表我们的标签(B,E这些标签,代表一个词语的开始,或者中间等等)
应用到命名实体识别中,v代表词语,是可以观察的。q代表我们的标签(标签代表着地点词,时间词这些)
From: NLP - 05. Tagging Problems, and HMM
HMM 算是生成模型中的一种。
这里用到的是Trigram Hidden Markov Models: 受最近的两个单词的影响,也就是分析三个单词之间的关系。
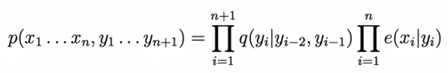

写成一个归纳的形式,如下:

xi: Term.
yi: Named Entity Recognition.
HMM的三大问题
我爱自然语言处理 - HMM
Link: http://www.52nlp.cn/category/hidden-markov-model/page/4
Link 三大问题
-
Evaluation problem - 计算问题
- Evaluation problem answers the question: what is the probability that a particular sequence of symbols is produced by a particular model?
- For evaluation we use two algorithms: the forward algorithm or the backwards algorithm (DO NOT confuse them with the forward-backward algorithm).
-
Decoding problem - 解码问题
- Decoding problem answers the question: Given a sequence of symbols (your observations) and a model, what is the most likely sequence of states that produced the sequence.
- For decoding we use the Viterbi algorithm.
-
Training problem - 学习问题
- Training problem answers the question: Given a model structure and a set of sequences, find the model that best fits the data.
- For this problem we can use the following 3 algorithms:
- MLE (maximum likelihood estimation)
- Viterbi training (DO NOT confuse with Viterbi decoding)
- Baum Welch = forward-backward algorithm
考虑一个村庄,所有村民都健康或发烧,只有村民医生才能确定每个人是否发烧。医生通过询问患者的感受来诊断发烧。村民只能回答说他们觉得正常,头晕或感冒。
医生认为,他的患者的健康状况作为离散的马可夫链。 “健康”和“发烧”有两个状态,但医生不能直接观察他们;健康与发烧的状态是隐藏的。每天都有机会根据患者的健康状况,病人会告诉医生他/她是“正常”,“感冒”还是“头昏眼花”。(正常,感冒,还是晕眩是我们前面说的观测序列)
观察(正常,感冒,晕眩)以及隐藏的状态(健康,发烧)形成隐马尔可夫模型(HMM),并可以用Python编程语言表示如下:
obs = ('normal', 'cold', 'dizzy')
states = ('Healthy', 'Fever')
start_p = {'Healthy': 0.6, 'Fever': 0.4} #医生对患者首次访问时HMM所处的状态的信念(他知道患者往往是健康的)
trans_p = {
'Healthy' : {'Healthy': 0.7, 'Fever': 0.3},
'Fever' : {'Healthy': 0.4, 'Fever': 0.6}
}
emit_p = {
'Healthy' : {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
'Fever' : {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6}
}
那么用图来表示上面的例子可以如下表示:
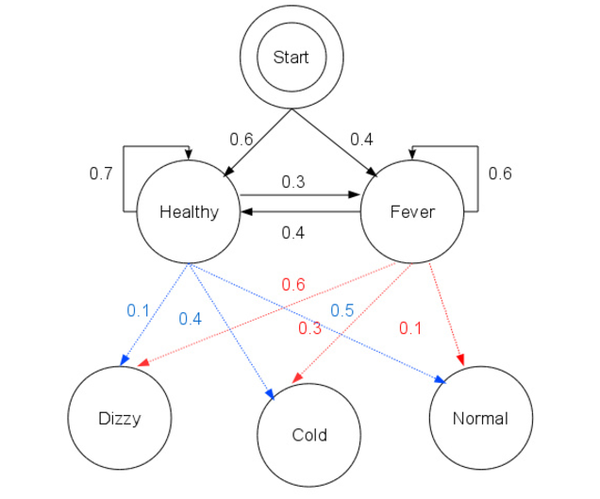
第一个问题 - 计算问题
求,给定模型的情况下,求某种观测序列出现的概率。
比如,给定的HMM模型参数已知,求出三天观察是 (Dizzy,Cold,Normal) 的概率是多少?
对应的HMM模型参数已知的意思,就是说的A,B,pi矩阵是已经知道的。
第二个问题 - 学习问题
已知观测序列是(Dizzy,Cold,Normal),需要求出HMM的参数问题。
也就是我们上面说的 A, B, PI 三个矩阵参数
重点,采用EM逼近。
Note, since the EM algorithm is a gradient-based optimization method, it will generally get stuck in local optima. You should in general try to run fit with various initializations and select the highest scored model.
You can use the monitor_ attribute to diagnose convergence.
第三个问题 - 解码问题
我们知道了观测序列是(Dizzy,Cold,Normal),也知道了HMM的参数,让我们求出造成这个观测序列最有可能对应的状态序列。
比如说是(Healthy,Healthy,Fever)还是(Healthy,Healthy,Healthy)。
Jeff: 直观的brute force方法,求出所有的组合,然后求概率,概率最大的序列就是解。
实践出真知
"""
Sampling from HMM
-----------------
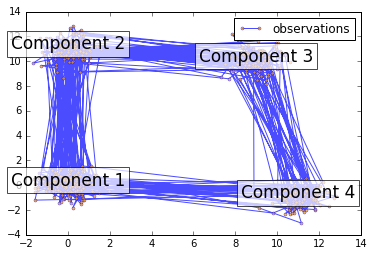
This script shows how to sample points from a Hiden Markov Model (HMM):
we use a 4-components with specified mean and covariance.
The plot show the sequence of observations generated with the transitions
between them. We can see that, as specified by our transition matrix,
there are no transition between component 1 and 3.
"""
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from hmmlearn import hmm
##############################################################
# Prepare parameters for a 4-components HMM
# Initial population probability
startprob = np.array([0.6, 0.3, 0.1, 0.0])
# The transition matrix, note that there are no transitions possible
# between component 1 and 3
transmat = np.array([[0.7, 0.2, 0.0, 0.1],
[0.3, 0.5, 0.2, 0.0],
[0.0, 0.3, 0.5, 0.2],
[0.2, 0.0, 0.2, 0.6]])
# The means of each component
means = np.array([[0.0, 0.0],
[0.0, 11.0],
[9.0, 10.0],
[11.0, -1.0]])
# The covariance of each component
covars = .5 * np.tile(np.identity(2), (4, 1, 1))
# Build an HMM instance and set parameters
model = hmm.GaussianHMM(n_components=4, covariance_type="full")
# Instead of fitting it from the data, we directly set the estimated
# parameters, the means and covariance of the components
model.startprob_ = startprob
model.transmat_ = transmat
model.means_ = means
model.covars_ = covars
###############################################################
# Generate samples
X, Z = model.sample(500)
# Plot the sampled data
plt.plot(X[:, 0], X[:, 1], ".-", label="observations", ms=6,
mfc="orange", alpha=0.7)
# Indicate the component numbers
for i, m in enumerate(means):
plt.text(m[0], m[1], 'Component %i' % (i + 1),
size=17, horizontalalignment='center',
bbox=dict(alpha=.7, facecolor='w'))
plt.legend(loc='best')
plt.show()
Result:
Finance module的库有问题: link
The finance module has been split out into its own package https://github.com/matplotlib/mpl_finance and deprecated in matplotlib. Any further development will take place in https://github.com/matplotlib/mpl_finance can you report the issue there? The finance module has been deprecated because non of the matplotlib developers are interested in maintaining it and mpl_finance is currently almost un maintained. It might also be worth checking out https://pypi.python.org/pypi/yahoo-finance as an alternative solution
"""
Gaussian HMM of stock data
--------------------------
This script shows how to use Gaussian HMM on stock price data from
Yahoo! finance. For more information on how to visualize stock prices
with matplotlib, please refer to ``date_demo1.py`` of matplotlib.
"""
from __future__ import print_function
import datetime
import numpy as np
from matplotlib import cm, pyplot as plt
from matplotlib.dates import YearLocator, MonthLocator
try:
from matplotlib.finance import quotes_historical_yahoo_ochl
except ImportError:
# For Matplotlib prior to 1.5.
from matplotlib.finance import (
quotes_historical_yahoo as quotes_historical_yahoo_ochl
)
from hmmlearn.hmm import GaussianHMM
print(__doc__)
###############################################################################
# Get quotes from Yahoo! finance
quotes = quotes_historical_yahoo_ochl("^GSPC", datetime.date(2012, 1, 1), datetime.date(2015, 1, 6))
sp = quotes_historical_yahoo_ochl("^GSPC", datetime.date(2012, 1, 1), datetime.date(2015, 1, 6), asobject=True, adjusted=True)
# Unpack quotes
dates = np.array([q[0] for q in quotes], dtype=int)
close_v = np.array([q[2] for q in quotes])
volume = np.array([q[5] for q in quotes])[1:]
# Take diff of close value. Note that this makes
# ``len(diff) = len(close_t) - 1``, therefore, other quantities also
# need to be shifted by 1.
diff = np.diff(close_v)
dates = dates[1:]
close_v = close_v[1:]
# Pack diff and volume for training.
X = np.column_stack([diff, volume])
###############################################################################
# Run Gaussian HMM
print("fitting to HMM and decoding ...", end="")
# Make an HMM instance and execute fit
model = GaussianHMM(n_components=4, covariance_type="diag", n_iter=1000).fit(X)
# Predict the optimal sequence of internal hidden state
hidden_states = model.predict(X)
print("done")
###############################################################################
# Print trained parameters and plot
print("Transition matrix")
print(model.transmat_)
print()
print("Means and vars of each hidden state")
for i in range(model.n_components):
print("{0}th hidden state".format(i))
print("mean = ", model.means_[i])
print("var = ", np.diag(model.covars_[i]))
print()
fig, axs = plt.subplots(model.n_components, sharex=True, sharey=True)
colours = cm.rainbow(np.linspace(0, 1, model.n_components))
for i, (ax, colour) in enumerate(zip(axs, colours)):
# Use fancy indexing to plot data in each state.
mask = hidden_states == i
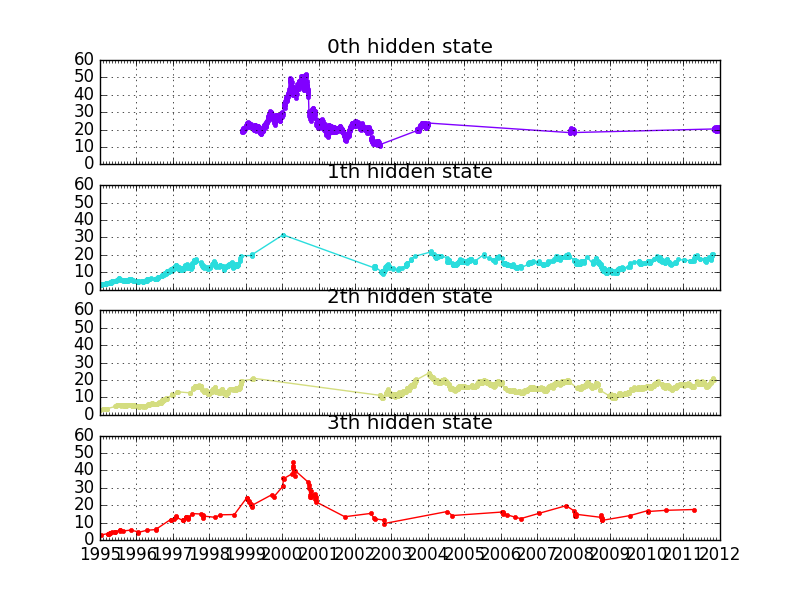
ax.plot_date(dates[mask], close_v[mask], ".-", c=colour)
ax.set_title("{0}th hidden state".format(i))
# Format the ticks.
ax.xaxis.set_major_locator(YearLocator())
ax.xaxis.set_minor_locator(MonthLocator())
ax.grid(True)
plt.show()
Out:
Transition matrix [[ 9.79220773e-01 2.57382344e-15 2.72061945e-03 1.80586073e-02] [ 1.12216188e-12 7.73561269e-01 1.85019044e-01 4.14196869e-02] [ 3.25313504e-03 1.12692615e-01 8.83368021e-01 6.86228435e-04] [ 1.18741799e-01 4.20310643e-01 1.18670597e-18 4.60947557e-01]] Means and vars of each hidden state 0th hidden state mean = [ 2.33331888e-02 4.97389989e+07] var = [ 6.97748259e-01 2.49466578e+14] 1th hidden state mean = [ 2.12401671e-02 8.81882861e+07] var = [ 1.18665023e-01 5.64418451e+14] 2th hidden state mean = [ 7.69658065e-03 5.43135922e+07] var = [ 5.02315562e-02 1.54569357e+14] 3th hidden state mean = [ -3.53210673e-01 1.53080943e+08] var = [ 2.55544137e+00 5.88210257e+15]
“纸上得来终觉浅,绝知此事要躬行”,在继续翻译《HMM学习最佳范例》之前,这里先补充几个不同程序语言实现的HMM版本,主要参考了维基百科。读者有兴趣的话可以研究一下代码,这样对于HMM的学习会深刻很多!
C语言版:
1、 HTK(Hidden Markov Model Toolkit):
HTK是英国剑桥大学开发的一套基于C语言的隐马尔科夫模型工具箱,主要应用于语音识别、语音合成的研究,也被用在其他领域,如字符识别和DNA排序等。HTK是重量级的HMM版本。
HTK主页:http://htk.eng.cam.ac.uk/
2、 GHMM Library:
The General Hidden Markov Model library (GHMM) is a freely available LGPL-ed C library implementing efficient data structures and algorithms for basic and extended HMMs.
GHMM主页:http://www.ghmm.org/
3、 UMDHMM(Hidden Markov Model Toolkit):
Hidden Markov Model (HMM) Software: Implementation of Forward-Backward, Viterbi, and Baum-Welch algorithms.
这款属于轻量级的HMM版本。
UMDHMM主页:http://www.kanungo.com/software/software.html
Java版:
4、 Jahmm Java Library (general-purpose Java library):
Jahmm (pronounced "jam"), is a Java implementation of Hidden Markov Model (HMM) related algorithms. It's been designed to be easy to use (e.g. simple things are simple to program) and general purpose.
Jahmm主页:http://code.google.com/p/jahmm/
Malab版:
5、 Hidden Markov Model (HMM) Toolbox for Matlab:
This toolbox supports inference and learning for HMMs with discrete outputs (dhmm's), Gaussian outputs (ghmm's), or mixtures of Gaussians output (mhmm's).
Matlab-HMM主页:http://www.cs.ubc.ca/~murphyk/Software/HMM/hmm.html
Common Lisp版:
6、CL-HMM Library (HMM Library for Common Lisp):
Simple Hidden Markov Model library for ANSI Common Lisp. Main structures and basic algorithms implemented. Performance speed comparable to C code. It's licensed under LGPL.
CL-HMM主页:http://www.ashrentum.net/jmcejuela/programs/cl-hmm/
Haskell版:
7、The hmm package (A Haskell library for working with Hidden Markov Models):
A simple library for working with Hidden Markov Models. Should be usable even by people who are not familiar with HMMs. Includes implementations of Viterbi's algorithm and the forward algorithm.
Haskell-HMM主页:http://hackage.haskell.org/cgi-bin/hackage-scripts/package/hmm
注:Haskell是一种纯函数式编程语言,它的命名源自美国数学家Haskell Brooks Curry,他在数学逻辑方面上的工作使得函数式编程语言有了广泛的基础。
是否还有C++版、Perl版或者Python版呢?欢迎补充!
注:原创文章,转载请注明出处“我爱自然语言处理”:www.52nlp.cn
本文链接地址:http://www.52nlp.cn/several-different-programming-language-version-of-hmm


 浙公网安备 33010602011771号
浙公网安备 33010602011771号