[Pandas] 01 - A guy based on NumPy
主要搞明白NumPy “为什么快”？
一、学习资源
- Panda 中文
- 易百教程
- 远程登录Jupyter笔记本
- "第六章、矩阵和矢量计算" from《Python高性能编程》
- 系统级性能分析工具perf的介绍与使用
二、效率进化
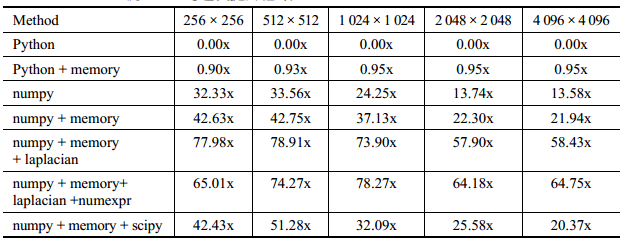
NumPy 底层进行了不错的优化。
In [11]:
loops = 25000000
from math import *
# 策略1：对每一个元素依次进行计算
a = range(1, loops)
def f(x):
return 3 * log(x) + cos(x) ** 2
%timeit r = [f(x) for x in a]
In [12]:
# 策略2：使用np
import numpy as np
a = np.arange(1, loops)
%timeit r = 3 * np.log(a) + np.cos(a) ** 2
In [13]:
# 策略3：numexpr方法，避免了数组在内存中复制
import numexpr as ne
ne.set_num_threads(1)
f = '3 * log(a) + cos(a) ** 2'
%timeit r = ne.evaluate(f)
In [14]:
# 策略4：再并发四线程
ne.set_num_threads(4) # 支持并发
%timeit r = ne.evaluate(f)
三、高级知识点
(a) numexpr
NumPy 虽然通过底层高度优化过的计算库可以实现接近C的高效计算，但在计算复杂且计算量庞大的时候多少还是有些嫌慢。Numexpr 库是最近发现的一个非常简单易用的 Numpy性能提升工具。
Goto: NumExpr: Fast numerical expression evaluator for NumPy
(b) cupy利用gpu加速
先安装cuda驱动：[CUDA] 00 - GPU Driver Installation & Concurrency Programming
再安装CuPy驱动：CuPy Installation
(c) PyPy 与 CPython
需要了解：PyPy和CPython的不同点。
CPython的思路
def add(x, y): return x + y if instance_has_method(x, '__add__') { return call(x, '__add__', y) // x.__add__ 里面又有一大堆针对不同类型的 y 的判断
} else if isinstance_has_method(super_class(x), '__add__' { return call(super_class, '__add__', y)
} else if isinstance(x, str) and isinstance(y, str) { return concat_str(x, y)
} else if isinstance(x, float) and isinstance(y, float) { return add_float(x, y)
} else if isinstance(x, int) and isinstance(y, int) { return add_int(x, y)
} else ...
Just In Time 编译
为何加速了呢？PyPy 执行的时候，发现执行了一百遍 add 函数，发现你 TM 每次都只传两个整数进来，那我何苦每次还给你做这么多计算。于是当场生成了一个类似 C 的函数：
int add_int_int(int x, int y) {
return x + y;
}
系统级性能剖析
一、原始实验
原始代码，作为之后的优化参照。
import numpy as np import time grid_size = (512,) def laplacian(grid, out): np.copyto(out, grid) np.multiply(out, -2.0, out) np.add(out, np.roll(grid, +1), out) np.add(out, np.roll(grid, -1), out) def evolve(grid, dt, out, D=1): laplacian(grid, out) np.multiply(out, D * dt, out) np.add(out, grid, out)
def run_experiment(num_iterations):
scratch = np.zeros(grid_size) grid = np.zeros(grid_size) block_low = int(grid_size[0] * .4) block_high = int(grid_size[0] * .5) grid[block_low:block_high] = 0.005 start = time.time() for i in range(num_iterations): evolve(grid, 0.1, scratch) grid, scratch = scratch, grid return time.time() - start
if __name__ == "__main__": run_experiment(500)
性能分析一：
$ sudo perf stat -e cycles,stalled-cycles-frontend,stalled-cycles-backend,instructions,cache-references,cache-misses,branches,branch-misses,task-clock,faults,minor-faults,cs,migrations -r 3 python diffusion_python_memory.py
Performance counter stats for '/usr/local/anaconda3/bin/python3 diffusion_numpy_memory.py' (3 runs): 358139881 cycles # 3.605 GHz ( +- 2.30% ) (65.11%) <not supported> stalled-cycles-frontend <not supported> stalled-cycles-backend 453383936 instructions # 1.27 insn per cycle ( +- 1.22% ) (82.56%) 22986206 cache-references # 231.400 M/sec ( +- 0.56% ) (82.71%) 2022121 cache-misses # 8.797 % of all cache refs ( +- 15.29% ) (83.90%) 100438152 branches # 1011.101 M/sec ( +- 1.59% ) (83.90%) 3004796 branch-misses # 2.99% of all branches ( +- 0.49% ) (84.38%) 99.34 msec task-clock # 0.996 CPUs utilized ( +- 4.31% ) 4984 faults # 0.050 M/sec ( +- 0.07% ) 4984 minor-faults # 0.050 M/sec ( +- 0.07% ) 1 cs # 0.007 K/sec ( +- 50.00% ) 0 migrations # 0.000 K/sec 0.09976 +- 0.00448 seconds time elapsed ( +- 4.49% )
二、利用内建优化代码
写在一起的好处是：短代码往往意味着高性能，因为容易利用内建优化机制。
def laplacian(grid): return np.roll(grid, +1) + np.roll(grid, -1) - 2 * grid
def evolve(grid, dt, D=1): return grid + dt * D * laplacian(grid)
性能分析二：cache-references非常大，但0.97指令减少才是重点。
Performance counter stats for '/usr/local/anaconda3/bin/python3 diffusion_numpy.py' (3 runs): 345131518 cycles # 3.368 GHz ( +- 2.05% ) (63.87%) <not supported> stalled-cycles-frontend <not supported> stalled-cycles-backend 441624002 instructions # 1.28 insn per cycle ( +- 0.41% ) (82.69%) 22383742 cache-references # 218.428 M/sec ( +- 0.44% ) (84.39%) 2334617 cache-misses # 10.430 % of all cache refs ( +- 4.03% ) (84.39%) 98647251 branches # 962.634 M/sec ( +- 1.17% ) (84.39%) 2950862 branch-misses # 2.99% of all branches ( +- 0.24% ) (82.97%) 102.48 msec task-clock # 0.998 CPUs utilized ( +- 2.02% ) 4978 faults # 0.049 M/sec ( +- 0.04% ) 4978 minor-faults # 0.049 M/sec ( +- 0.04% ) 1 cs # 0.007 K/sec ( +- 50.00% ) 0 migrations # 0.000 K/sec 0.10270 +- 0.00209 seconds time elapsed ( +- 2.04% )
三、降低内存分配、提高指令效率
找到 “正确的优化” 的点
我们使用 numpy降低了 CPU 负担，我们降低了解决问题所必要的内存分配次数。
事实上 evolve 函数有 93%的时间花费在 laplacian 函数中。
参见：[Optimized Python] 17 - Bottle-neck in performance
进一步优化
向操作系统进行请求所需的开销比简单填充缓存大很多。
填充一次缓存失效是一个在主板上优化过的硬件行为，而内存分配则需要跟另一个进程、内核打交道来完成。
（1）"+="运算符的使用减少了“不必要的变量内存分配”。
（2）roll_add替代过于全能的np.roll，以减少不必要的指令。
def roll_add(rollee, shift, out): if shift == 1: out[1:] += rollee[:-1] out[0] += rollee[-1] elif shift == -1: out[:-1] += rollee[1:] out[-1] += rollee[0] def laplacian(grid, out): np.copyto(out, grid) np.multiply(out, -2.0, out) roll_add(grid, +1, out) roll_add(grid, -1, out) def evolve(grid, dt, out, D=1): laplacian(grid, out) np.multiply(out, D * dt, out) np.add(out, grid, out
性能分析三：减低了内存缺页，提高了指令效率。
Performance counter stats for '/usr/local/anaconda3/bin/python3 diffusion_numpy_memory2.py' (3 runs): 314575986 cycles # 3.670 GHz ( +- 1.89% ) (62.67%) <not supported> stalled-cycles-frontend <not supported> stalled-cycles-backend 402037134 instructions # 1.28 insn per cycle ( +- 0.19% ) (81.33%) 18138094 cache-references # 211.611 M/sec ( +- 2.65% ) (81.94%) 2298500 cache-misses # 12.672 % of all cache refs ( +- 6.84% ) (84.68%) 88677913 branches # 1034.575 M/sec ( +- 0.68% ) (86.00%) 2885039 branch-misses # 3.25% of all branches ( +- 1.19% ) (84.71%) 85.71 msec task-clock # 0.997 CPUs utilized ( +- 1.86% ) 4974 faults # 0.058 M/sec ( +- 0.10% ) 4974 minor-faults # 0.058 M/sec ( +- 0.10% ) 0 cs # 0.004 K/sec ( +-100.00% ) 0 migrations # 0.000 K/sec 0.08596 +- 0.00163 seconds time elapsed ( +- 1.89% )
四、整体处理表达式
numexpr 的一个重要特点是它考虑到了 CPU 缓存。它特地移动数据来让各级CPU 缓存能够拥有正确的数据让缓存失效最小化。
（a）当我们增加矩阵的大小时，我们会发现 numexpr 比原生 numpy 更好地利用了我们的缓存。而且，numexpr 利用了多核来进行计算并尝试填满每个核心的缓存。
（b）当矩阵较小时，管理多核的开销盖过了任何可能的性能提升。
import numexpr as ne
def evolve(grid, dt, out, D=1): laplacian(grid, out) ne.evaluate("out*D*dt+grid", out=out)
性能分析四：减低了内存缺页，提高了指令效率。
Performance counter stats for '/usr/local/anaconda3/bin/python3 diffusion_numpy_memory2_numexpr.py' (3 runs): 389532813 cycles # 3.888 GHz ( +- 1.01% ) (65.40%) <not supported> stalled-cycles-frontend <not supported> stalled-cycles-backend 478293442 instructions # 1.23 insn per cycle ( +- 1.70% ) (82.72%) 23279515 cache-references # 232.372 M/sec ( +- 0.91% ) (82.89%) 2447425 cache-misses # 10.513 % of all cache refs ( +- 10.84% ) (83.77%) 103451737 branches # 1032.639 M/sec ( +- 1.21% ) (84.97%) 3324954 branch-misses # 3.21% of all branches ( +- 0.61% ) (82.97%) 100.18 msec task-clock # 1.000 CPUs utilized ( +- 5.75% ) 8591 faults # 0.086 M/sec ( +- 0.01% ) 8591 minor-faults # 0.086 M/sec ( +- 0.01% ) 12 cs # 0.123 K/sec ( +- 2.70% ) 3 migrations # 0.030 K/sec 0.10018 +- 0.00582 seconds time elapsed ( +- 5.81% )
五、利用现成的方案
直接使用scipy提供的接口。
from scipy.ndimage.filters import laplace def laplacian(grid, out): laplace(grid, out, mode='wrap')
性能分析五：可能过于通用而没有明显提升。
Performance counter stats for '/usr/local/anaconda3/bin/python3 diffusion_scipy.py' (3 runs): 346206970 cycles # 3.647 GHz ( +- 0.37% ) (63.49%) <not supported> stalled-cycles-frontend <not supported> stalled-cycles-backend 441742003 instructions # 1.28 insn per cycle ( +- 1.10% ) (81.74%) 21243859 cache-references # 223.757 M/sec ( +- 0.37% ) (82.77%) 2092136 cache-misses # 9.848 % of all cache refs ( +- 1.46% ) (84.55%) 96943942 branches # 1021.088 M/sec ( +- 0.80% ) (85.19%) 3120156 branch-misses # 3.22% of all branches ( +- 1.27% ) (84.00%) 94.94 msec task-clock # 0.997 CPUs utilized ( +- 11.09% ) 5156 faults # 0.054 M/sec ( +- 0.10% ) 5156 minor-faults # 0.054 M/sec ( +- 0.10% ) 0 cs # 0.004 K/sec ( +-100.00% ) 0 migrations # 0.000 K/sec 0.0952 +- 0.0106 seconds time elapsed ( +- 11.14% )
六、总结
看来，scipy没有大的必要，“定制的” 优化比较靠谱。
NumPy Data Structures
使用原生 List 作为 Array
In [1]:
v = [0.5, 0.75, 1.0, 1.5, 2.0] # vector of numbers
In [2]:
m = [v, v, v] # matrix of numbers
m
Out[2]:
In [3]:
m[1]
Out[3]:
In [4]:
m[1][0]
Out[4]:
In [5]:
v1 = [0.5, 1.5]
v2 = [1, 2]
m = [v1, v2]
c = [m, m] # cube of numbers
c
Out[5]:
In [6]:
c[1][1][0]
Out[6]:
In [7]:
v = [0.5, 0.75, 1.0, 1.5, 2.0]
m = [v, v, v]
m
Out[7]:
In [8]:
v[0] = 'Python'
m
Out[8]:
In [9]:
from copy import deepcopy
v = [0.5, 0.75, 1.0, 1.5, 2.0]
m = 3 * [deepcopy(v), ]
m
Out[9]:
In [10]:
v[0] = 'Python'
m
Out[10]:
使用 NumPy Arrays
In [11]:
import numpy as np
In [12]:
a = np.array([0, 0.5, 1.0, 1.5, 2.0])
type(a)
Out[12]:
In [13]:
a[:2] # indexing as with list objects in 1 dimension
Out[13]:
In [14]:
a.sum() # sum of all elements
Out[14]:
In [15]:
a.std() # standard deviation
Out[15]:
In [16]:
a.cumsum() # running cumulative sum
Out[16]:
In [17]:
a * 2
Out[17]:
In [18]:
a ** 2
Out[18]:
In [19]:
np.sqrt(a)
Out[19]:
In [20]:
b = np.array([a, a * 2])
b
Out[20]:
In [21]:
b[0] # first row
Out[21]:
In [22]:
b[0, 2] # third element of first row
Out[22]:
In [23]:
b.sum()
Out[23]:
In [24]:
b.sum(axis=0)
# sum along axis 0, i.e. column-wise sum
Out[24]:
In [25]:
b.sum(axis=1)
# sum along axis 1, i.e. row-wise sum
Out[25]:
In [26]:
c = np.zeros((2, 3, 4), dtype='i', order='C') # also: np.ones()
c
Out[26]:
In [27]:
d = np.ones_like(c, dtype='f16', order='C') # also: np.zeros_like()
d
Out[27]:
In [28]:
import random
I = 5000
In [29]:
%time mat = [[random.gauss(0, 1) for j in range(I)] for i in range(I)]
# a nested list comprehension
In [30]:
%time mat = np.random.standard_normal((I, I))
In [31]:
%time mat.sum()
Out[31]:
自定义 Arrays
In [32]:
dt = np.dtype([('Name', 'S10'), ('Age', 'i4'),
('Height', 'f'), ('Children/Pets', 'i4', 2)]) # 类似与数据库的表，定义列的属性；每列数据的类型是要确保一致的
s = np.array([('Smith', 45, 1.83, (0, 1)),
('Jones', 53, 1.72, (2, 2))], dtype=dt)
s
Out[32]:
In [33]:
s['Name']
Out[33]:
In [34]:
s['Height'].mean()
Out[34]:
In [35]:
s[1]['Age']
Out[35]:
Vectorization of Code
Basic Vectorization 向量化
In [36]:
r = np.random.standard_normal((4, 3))
s = np.random.standard_normal((4, 3))
In [37]:
r + s
Out[37]:
In [38]:
2 * r + 3
Out[38]:
In [39]:
s = np.random.standard_normal(3)
r + s
Out[39]:
In [40]:
# causes intentional error
# s = np.random.standard_normal(4)
# r + s
In [41]:
# r.transpose() + s
In [42]:
np.shape(r.T)
Out[42]:
In [43]:
def f(x):
return 3 * x + 5
In [44]:
f(0.5) # float object
Out[44]:
In [45]:
f(r) # NumPy array
Out[45]:
In [46]:
# causes intentional error
# import math
# math.sin(r)
In [47]:
np.sin(r) # array as input
Out[47]:
In [48]:
np.sin(np.pi) # float as input
Out[48]:
结构组织方式
In [49]:
x = np.random.standard_normal((5, 10000000))
y = 2 * x + 3 # linear equation y = a * x + b
C = np.array((x, y), order='C') # 按行统计快些
F = np.array((x, y), order='F') # 按列统计快些
x = 0.0; y = 0.0 # memory clean-up
In [50]:
C[:2].round(2) # 四舍五入
Out[50]:
In [51]:
%timeit C.sum()
In [52]:
%timeit F.sum()
In [53]:
%timeit C[0].sum(axis=0)
In [54]:
%timeit C[0].sum(axis=1)
In [55]:
%timeit F.sum(axis=0)
In [56]:
%timeit F.sum(axis=1)
In [57]:
F = 0.0; C = 0.0 # memory clean-up
End.
浙公网安备 33010602011771号