基于Douglas-Peucker算法对矢量数据简化
#### 基于Douglas-Peucker算法对矢量数据简化 ####
# 当原始的矢量数据因为形状复杂,包含的点较多时,会导致其文件体积较大,
# 如果我们需要在在线地图上叠加它们,太大体积的矢量数据不仅会拖慢网络传输速度,
# 也会给图形的渲染带来更大的压力,这时对矢量数据进行简化就非常有必要。
# 基于Douglas-Peucker算法,基于预先设定的阈值ϵ,在递归判断的过程中删掉所有小于ϵ的点
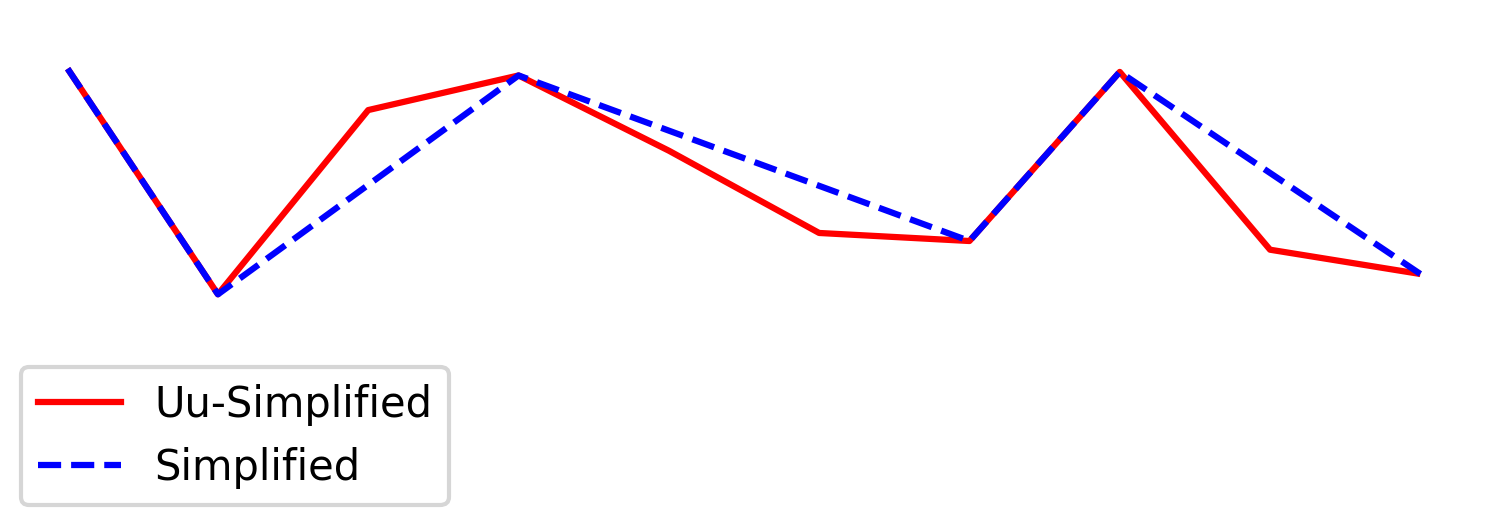
# 例如: 基于-1到1之间的均匀分布,创建一条上下波动的折线,然后进行简化
import numpy as np
import shapely
import geopandas as gpd
from matplotlib import pyplot as plt
import matplotlib.patches as mpatches
np.random.seed(10)# 固定随机数种子
# 创建线
line = shapely.geometry.LineString([(_, np.random.uniform(-1, 1)) for _ in range(10)])
# 绘制简化前
ax = gpd.GeoSeries([line]).plot(color='red')
# 绘制简化后
ax = gpd.GeoSeries([line]).simplify(tolerance=0.5).plot(color='blue',
ax=ax,
linestyle='--')
# 制作图例映射对象列表
LegendElement = [plt.Line2D([], [], color='red', label='Uu-Simplified'),
plt.Line2D([], [], color='blue', linestyle='--', label='Simplified')]
# 将制作好的图例映射对象列表导入legend()中,并配置相关参数
ax.legend(handles=LegendElement,
loc='lower left',
fontsize=10)
ax.set_ylim((-2.5, 1))
ax.axis('off')
plt.savefig('VectorLineSimplify.png', dpi=300, bbox_inches='tight', pad_inches=0)
plt.show()#展示
个人学习记录





 浙公网安备 33010602011771号
浙公网安备 33010602011771号