第一章笔记 of 《机器学习基石》-林轩田 (更新中)
最近开始入门机器学习,现在跟着台大林轩田老师的《机器学习基石》网课以及配套的课本《Learning From Data - A Short Course》。在每周固定抽时间看网课 / 看课本 / 做习题以外,还会通过在本博客连载的形式,记录、写下在学习的过程当中遇见的难懂问题和相关笔记。一步一步慢慢来,希望能像写了四五年的日记一样坚持做下来。
此文是有关《机器学习基石》笔记的第一篇,内容有关PLA算法(perceptron learning algorithm,感知学习算法)。
目录:
PLA算法,即Perceptron Learning Alogorithm,感知学习算法。它是线性的二元分类器(Linear binary classifier),能够把给出的数据集合(线性可分的,Linear Separable)分成两组。对于一个线性可分的数据集合,PLA算法能够找到分割该数据集合的划分。
什么是“线性可分”的呢?对于2D的情况就是“能够找到一条线,该线能完全切割、分离两群”,如下图所示:
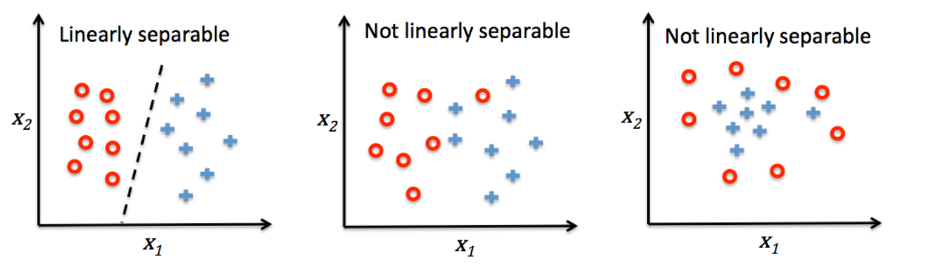
对于3D的情况就是“在三维空间中,能够找到一个平面,该平面能完全切割、分离两个群”。在本博文中只讨论2D的情况。
首先介绍PLA的公式:
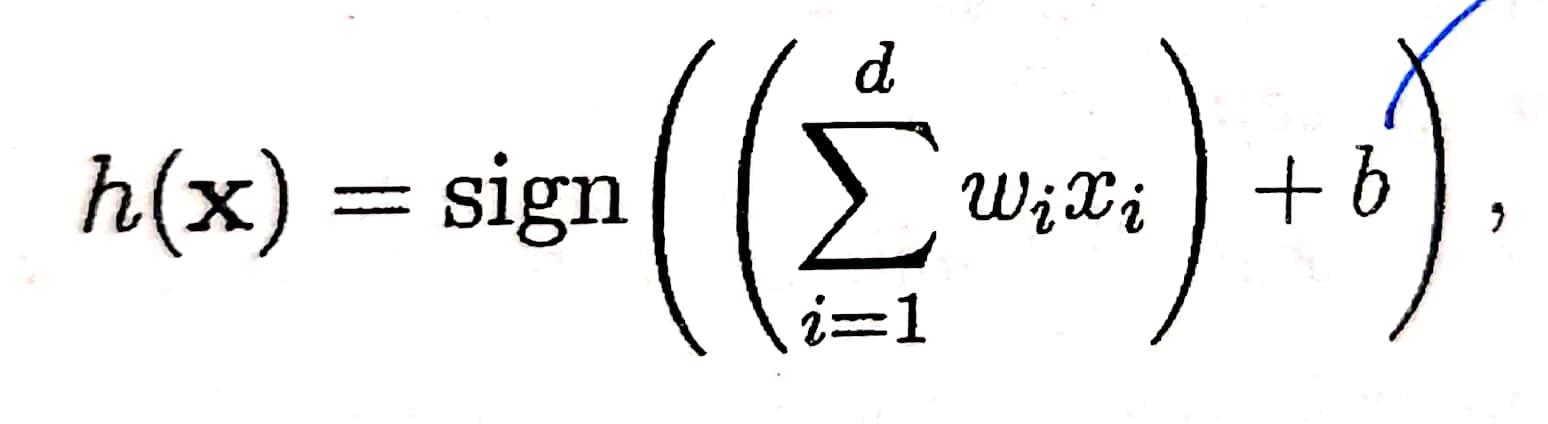
其中,
$w_i$:向量 $\vec{w}$ 的第 i 个分量。向量 $\vec{w}$ 是权重向量,其一共有 d 个分量(d维向量)。
$x_i$:向量 $\vec{x}$ 的第 i 个分量。向量 $\vec{x}$ 是输入向量(input vector),其一共有 d 个分量(d维向量)。
$b$:门槛值(threshold)。
sign( ):一个函数,输出值为1或-1。当权重向量与输入向量相乘所得之值( $\sum_{i=1}^{d}{(w_ix_i)}$ ) > 门槛值,sign( )函数输出1;若 < 门槛值,sign( )函数输出-1。因此,h(x)函数值或者为1,或者为-1。
关于PLA公式的简化,可以设 $w_0$ = -b(负的门槛值),相应地固定设置 $x_0$ = 1,从而将PLA公式化简成为:
$$h(x)\ =\ sign(\ \sum_{i=0}^{d}{(w_ix_i)}\ )\ =\ sign(w^Tx)$$
举一个应用到了以上公式的、具有实际意义的例子。银行在审核信用卡的申请时,需要综合考虑信用卡申请者的许多因素,包括:申请人的薪水($x_1$)、在当地居住时间($x_2$)、负债额度($x_3$)、……,某一个人的这些需要综合考虑的因素指标,量化为数字,组合在一起,就成为了一个输入向量,各个指标就是该输入向量的分量。
因为各项因素指标的重要性不同,所以银行需要为输入向量的各个分量,配给不同的权重值。当输入向量的每一分量 * 该分量对应的权重值,最终加和,达到了某一个门槛值,银行便允许这个人的信用卡申请(sign( ) = 1);没有达到门槛值,则拒绝这个人的信用卡申请(sign( ) = -1 )。
在这里,每一分量对应的权重值,就是$w_i$(i = 1,2,3,...,d),这些权重值组合在一起,形成权重向量 $\vec{w}$;门槛值存储在 $\vec{w}$ 之中的 $w_0$ 内。
二维平面上的点直观,有助于理解PLA算法。针对二维平面的PLA算法,能够把线性可分的两个点群,进行分割。
既然是二维平面,所以权重向量、输入向量的维度都是2(不算第0位的话,只有2个分量),
即$\vec{w} = w_0 + w_1 + w_2$; $\vec{x} = x_0 + x_1 + x_2$,其中 $x_1$ 和 $x_2$ 是向量 $\vec{x}$ 在一个二维平面的坐标值(相当于对应着(x, y) )。
在二维平面上,有线性可分的两个点群,一种点群是“圈圈点”,它的y值是+1;一种点群是“叉叉点”,它的y值是-1。

PLA算法的目的在于:在这个二维平面中,找到这样一条直线 h,该直线 h 能够将圈圈点和叉叉点划分在两边。
怎么做呢?下图是PLA算法的流程:

这是一个迭代的流程,在第 t 次迭代中(t = 0, 1, 2, ...),执行:
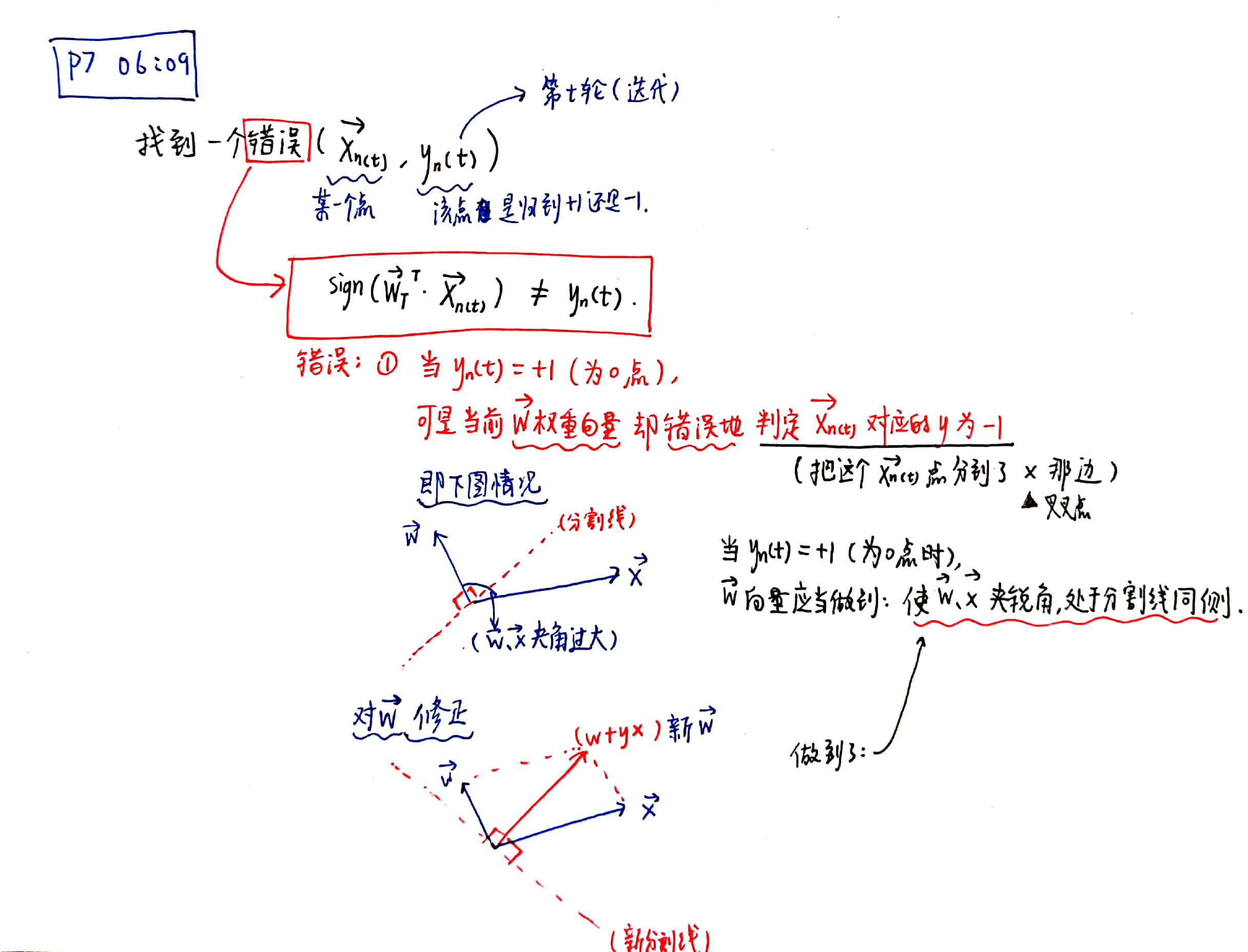
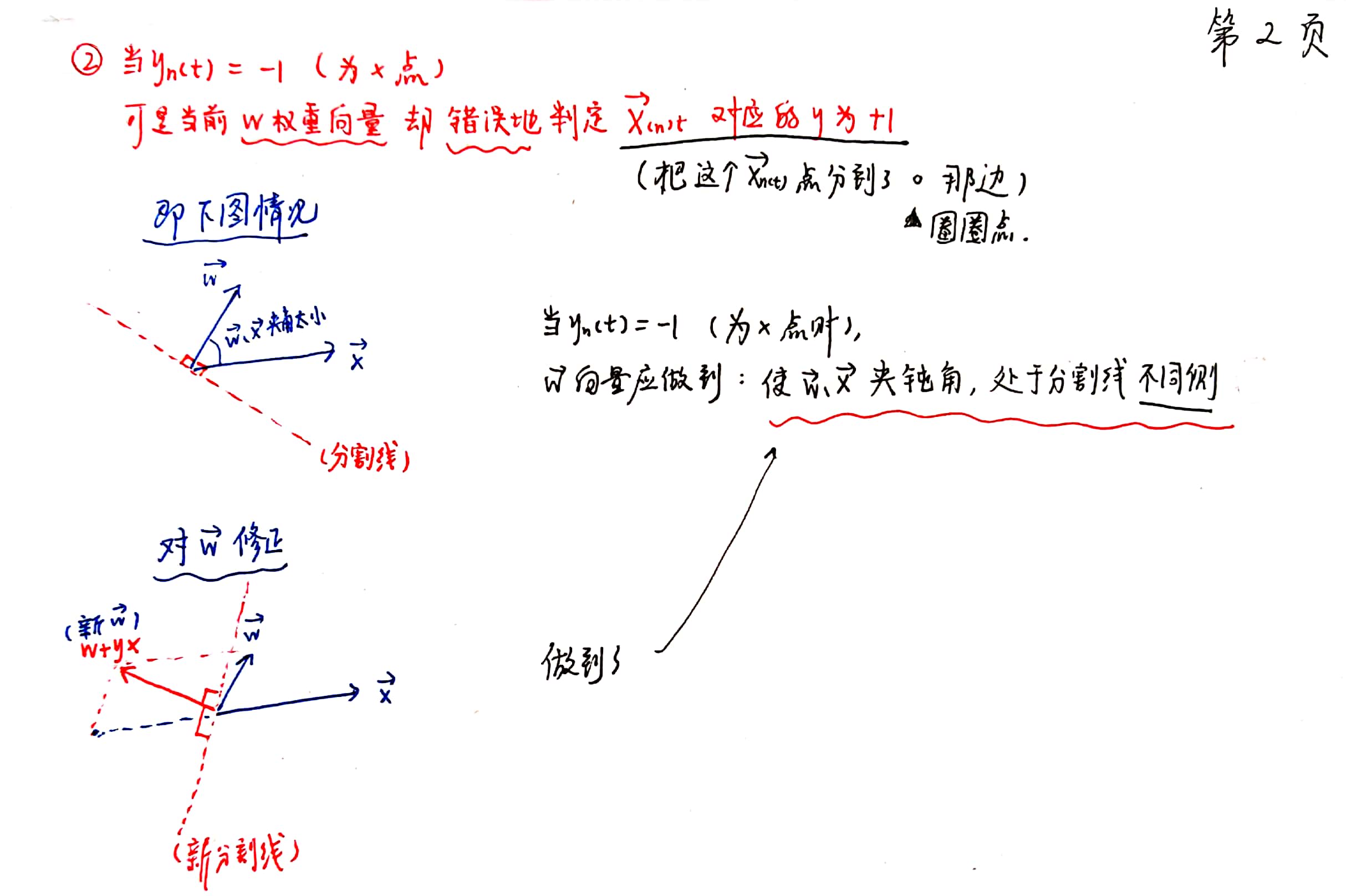
① 找到一个错误的点。
②对权重向量进行修正。具体修正公式为: $\vec{w_{t+1}}\gets\ \vec{w_t}\ +\ y_{n(t)}{\vec{x}}_{n(t)}$
其中,${\vec{x}}_{n(t)}$ 是输入向量,即二维平面上的某一个点;$y_{n(t)}$ 是这一个点自身固有的标签,或者为+1,或者为-1。
当 $\ sign(w^Tx)$ ≠ $y_{n(t)}$ ,即在当前迭代的PLA算法的权重下,计算出来的某一个点的标签值,与该点自身固有的标签值不相同 - 那么,这就是一个“错误的点”。这一内容体现在二维平面上,就是 $\vec{w}$ 与 $\vec{x}$ 之间夹角的问题。请见以下笔记内容。
会。以下为详细证明过程:





 浙公网安备 33010602011771号
浙公网安备 33010602011771号