CF344B Simple Molecules - 题解

这道题可以用 \(O(1)\) 的三元一次方程来做。

我们设 \(1\) 号节点的度为 \(a\)，\(2\) 号节点的度为 \(b\)，\(3\) 号节点的度为 \(c\)；再设 \(1,2\) 号节点有 \(x\) 条连边，\(2,3\) 号节点有 \(y\) 条连边，\(3,1\) 号节点有 \(z\) 条连边。用一张图来表示就是：

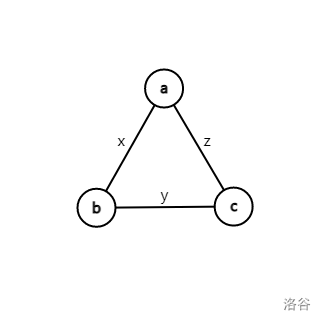
因为节点的度就是它所连边的条数，所以 \(1\) 号点的度也为 \(x+z\)，\(2,3\) 号分别为 \(x+y\) 和 \(y+z\)。即

\[\begin{cases} a=x+z\\ b=x+y\\ c=y+z \end{cases}\]

只需要解出这个方程了 （应该都会解三元一次方程吧）。三个式子相加得：

\[a+b+c=2x+2y+2z \]

交换式子两边并同时除以 \(2\) 得：

\[x+y+z=\frac{a+b+c}{2} \]

把这个式子减去 \(x+z=a\) 得到：\(y=\frac{a+b+c}{2}-a\)，\(x,z\) 也可以同理得到，即：

\[\begin{cases} x=\frac{a+b+c}{2}-c\\ y=\frac{a+b+c}{2}-a\\ z=\frac{a+b+c}{2}-b \end{cases}\]

然后直接输出 \(x,y,z\) 即可。

还要注意 Impossible 的情况：

• \(a+b+c\) 不是偶数，即不被 \(2\) 整除。
• \(x,y,z\) 中任意一个算出来是个负数。

这两种情况需要进行判断。

这样，就可以用 \(O(1)\) 的时间复杂度得到答案了，根本不用 \(O(\max(a,b,c))\) 的循环。

代码

#include<cstdio>
using namespace std;
int a,b,c;
int main()
{
	scanf("%d%d%d",&a,&b,&c);
	int sum=(a+b+c)>>1;		//(a+b+c)>>1 等价于 (a+b+c)/2 
	int x=sum-c,y=sum-a,z=sum-b;
	if((a+b+c)&1||x<0||y<0||z<0)	//(a+b+c)&1 等价于 (a+b+c)%2 
		printf("Impossible\n");
	else printf("%d %d %d\n",x,y,z);
	return 0;
}

\[\Large\frak{The\ End} \]

---

2022-07-20 23:20 撰写于洛谷，2025-08-29 20:30 迁移至博客园。