题解：QOJ-6322 / The 1st Universal Cup. Stage 12: Ōokayama - F. Forestry

前言

线段树合并优化 DP 神题，虽然偏模板但整体难度较高。

前置知识：动态规划、树状 DP、线段树动态开点、线段树合并。

题目链接：点击此处。

DP 状态表示

首先这个题有一个极其诡异的 DP 状态，别问我怎么知道的，问就是各种试出来的。

先将所有权值排序，相当于离散化，注意这里为了简便用了一种特殊的离散化：不去重的离散化，以保证（或假装）每个点的权值都不同。

然后设 \(f_{x,i}\) 表示：把以 \(x\) 为根的子树看作一个单独的子问题，对于所有 \(2^{sz(x)-1}\) 种切边方式（\(sz(x)\) 表示子树点数），找出所有包含 \(x\) 的块，这些块中第 \(i\) 个权值作为最小值出现的总次数。

举个例子（假设结点 \(i\) 的权值即为 \(i\)）：

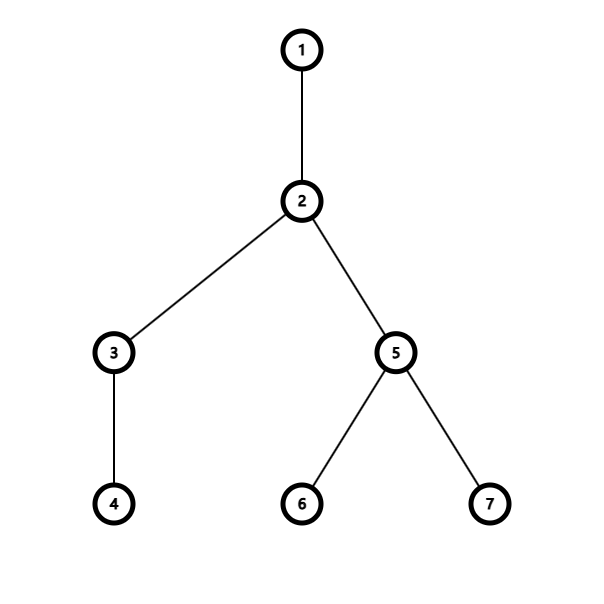
image

在这棵树中，把以 \(2\) 为根的子树看作一个全新的子问题。那么对于某一种切法，假设这样：

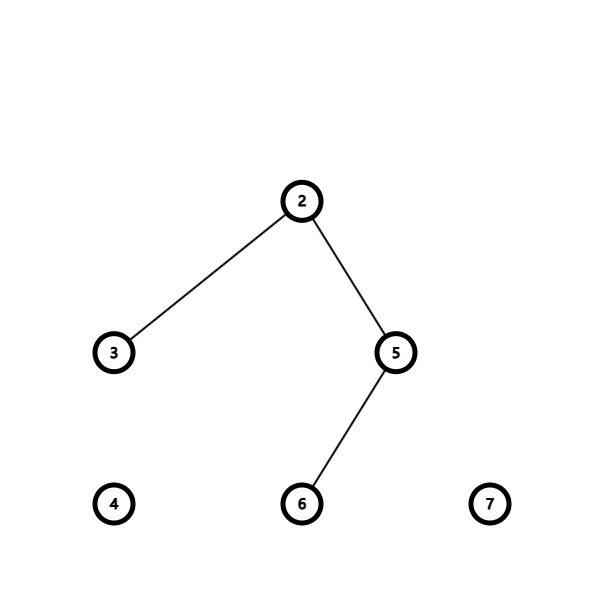
image

那么这其中 \(2\) 所属「\(3-2-5-6\)」连通块，最小值为 \(2\)。这就是一种能得到 \(2\) 的切边方案，所以对 \(f_{2,2}\) 就有了 \(1\) 的贡献。

最后的答案也就可以通过它来表示了：

\[\sum_{x \in V} \left( 2^{n-sz(x)-1} \times \sum_{i=1}^{n} f_{x,i} \times v_i \right) \]

（\(V\) 为结点集合，\(v_i\) 表示特殊离散化后第 \(i\) 个权值；\(2^{n-sz(x)-1}\) 表示全树中除去该子树和子树根与其父结点那条边（不能选）的其它边的所有取值可能，每一种可能都可以和子树内已有所有答案组合）

这样就可以不重不漏地覆盖所有联通块的情况。

DP 方程

然后这个 DP 的方程也不简单，既然是树状 DP，那么就考虑结点 \(x\) 新加入一个子结点 \(y\) 的贡献。分以下两种可能。

一，\(x\) 和 \(y\) 之间连边。那么对于每一对 \(i,j\)，都对 \(f_{x, \min(i,j)}\) 造成了 \(f_{x,i} \times f_{y,j}\) 的贡献。略微推一下式子，得到这种情况对 \(f_{x,i}\) 的贡献为：

\[f_{x,i} \times \sum_{j>i} f_{y,j} + f_{y,i} \times \sum_{j>i} f_{x,j} \]

（其实还有一个 \(f_{x,i} \times f_{y,i}\) 的项，但是由于先前的特殊离散化，这两个不可能同时有值，所以乘积必为 \(0\)，也就可以省掉了。那个特殊离散化的目的就是为了简化掉这一项。）

二、\(x\) 和 \(y\) 之间不连边。在这种情况下，\(y\) 子树内的任意一种切边方式，和 \(x\) 已有的切边方式组合都能组合出一个答案，而这个答案和没有 \(y\) 时（也就是 \(f_x\) 当前）是一致的。所以这里对 \(f_{x,i}\) 的贡献为：

\[f_{x,i} \times 2^{sz(y)-1} \]

其中 \(sz(y)-1\) 表示 \(y\) 子树内边数，\(2^{sz(y)-1}\) 就是 \(y\) 子树内切边方案数量。

以上两个式子合并起来就得到：

\[f'_{x,i} = f_{x,i} \times \left( \sum_{j>i} f_{y,j} + 2^{sz(y)-1} \right) + f_{y,i} \times \sum_{j>i} f_{x,j} \]

数据结构优化

有了这个恶臭的方程，观察到里面有形如后缀的玩意，所以尝试用线段树合并优化 DP 求解。

（好吧，我承认我只是觉得这道题和另一道题的方程形式有点像才尝试用线段树合并优化的。虽然具体为什么用不太清楚，但还是建议也做一做那道题。）

对每个结点 \(x\) 开一个动态开点线段树，维护 \(f_{x}\) 相关信息，其中需要有以下几个数据：

  • sum：区间内 \(f_{x,i}\) 值的和，用作转移方程；
  • dat：区间内 \(f_{x,i} \times v_i\) 值的和，用作计算最终答案；

除此以外，该线段树还需要支持乘法，所以还需要一个乘法延迟标记。

接下来是整个算法的核心：线段树合并操作，这个操作可以快速将 \(f_y\) 直接合并进 \(f_x\) 中去。

回忆一下线段树合并的流程：递归合并直到某一线段树上该区间为空，或者找到叶节点。又因为合并到叶节点还都不为空在此算法里是不可能的（还是因为特殊离散化），所以只考虑合并到某区间为空的情况。

上面的方程中，单独一项的 \(f\) 顺序不变，只是乘上了一个倍率，而这个倍率是一个后缀和的形式，这个后缀和在线段树合并的递归过程中可以方便地维护。

那么在遇到某一线段树（假设为 \(x\) 所属线段树）上该区间为空时，区间内所有的 \(f_{x,j}\) 就都是 \(0\)，这整个区间内的后缀和 \(\sum_{j>i} f_{x,j}\)（同时也是 \(f_{y,i}\) 所乘系数）就确定为了同一个值，这个值已经在递归的过程中维护成功了，所以我们只需要将 \(y\) 所属线段树上该区间同时乘上它再返回即可。另一边的 \(x\) 所属线段树乘法同理。

代码长这样，\(p\)、\(q\) 即代表刚才所说 \(x\)、\(y\) 所属线段树。注意在调用时 pmul 有一个 \(2^{sz(y)-1}\) 的初始值以符合上面的方程。

int Merge(int p, int q, int l, int r, LL pmul, LL qmul)
{
	if(!p && !q) return 0;
	if(!p)
	{
		tr[q].mul(qmul);
		return q;
	}
	if(!q)
	{
		tr[p].mul(pmul);
		return p;
	}
	pushdown(p), pushdown(q);
	int mid = l + r >> 1;
	LL spr = tr[tr[p].rs].sum, sqr = tr[tr[q].rs].sum;
	tr[p].ls = Merge(
		tr[p].ls, tr[q].ls,
		l, mid,
		(pmul + sqr) % MOD, (qmul + spr) % MOD
	);
	tr[p].rs = Merge(
		tr[p].rs, tr[q].rs,
		mid + 1, r,
		pmul, qmul
	);
	pushup(p);
	return p;
}

代码

对于这题的空间计算，因为代码开头时 Add 了 \(n\) 次，而每次从根节点走到叶节点，最多走了 \(\lceil \log_2 n \rceil + 1\)（也就是线段树的高度）个节点，所以线段树总空间应该开成 \(n(\lceil \log_2 n \rceil + 1)\)。

完整代码如下，接近 \(4\)KB。

#include <cstdio>
#include <cstdlib>
#include <algorithm>

using namespace std;

namespace IO{
const int SIZE=1<<20; char buf[SIZE],*p1=buf,*p2=buf;
#ifndef JC_LOCAL
inline char _getchar() {return (p1==p2&&(p2=(p1=buf)+fread(buf,1,SIZE,stdin),p1==p2))?EOF:*p1++;}
#else
inline char _getchar() {return getchar();}
#endif
template<typename TYPE> void read(TYPE &x)
{
	x=0; bool neg=false; char ch=_getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')neg=true;ch=_getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+(ch^'0');ch=_getchar();}
	if(neg){x=-x;} return;
}
template<typename TYPE> void write(TYPE x)
{
	if(!x){putchar('0');return;} if(x<0){putchar('-');x=-x;}
	static int sta[55];int statop=0; while(x){sta[++statop]=x%10;x/=10;}
	while(statop){putchar('0'+sta[statop--]);} return;
}
template<typename TYPE> void write(TYPE x,char ch){write(x);putchar(ch);return;}
} using IO::read; using IO::write;

typedef long long LL;

const int N = 3e5 + 5, logN = 19 + 1;
const LL MOD = 998244353;
int n; LL ans;

LL raw[N], sorted[N];
int disc[N], dcnt[N];
void Disc()
{
	copy(raw + 1, raw + n + 1, sorted + 1);
	sort(sorted + 1, sorted + n + 1);
	for (int i = 1; i <= n; i++)
	{
		int num = lower_bound(sorted + 1, sorted + n + 1, raw[i]) - sorted;
		disc[i] = num + dcnt[num];
		dcnt[num]++;
	}
	return;
}

struct Allan{
	int to, nxt;
}edge[N << 1];
int head[N], eidx;
inline void add(int x, int y)
{
	edge[++eidx] = {y, head[x]};
	head[x] = eidx;
	return;
}

/*---------- Dynamic Segment Tree - Begin ----------*/ 

struct DynSegTree{
	int l, r; 
	LL sum, lzy, dat;
	int ls, rs;
	inline int mid() {return l + r >> 1;}
	inline bool is_leaf() {return l == r;}
	inline void mul(LL v)
	{
		(sum *= v) %= MOD;
		(dat *= v) %= MOD;
		(lzy *= v) %= MOD;
		return;
	}
}tr[N * logN];
int tridx, rt[N];

inline void check(int &p, int l, int r)
{
	if (!p)
	{
		p = ++tridx;
		tr[p] = {l, r, 0, 1, 0, 0, 0};
	}
	return;
}

inline void pushup(int p)
{
	int ls = tr[p].ls, rs = tr[p].rs;
	tr[p].sum = (tr[ls].sum + tr[rs].sum) % MOD;
	tr[p].dat = (tr[ls].dat + tr[rs].dat) % MOD;
	return;
}
inline void pushdown(int p)
{
	LL &lzy = tr[p].lzy;
	if (lzy != 1)
	{
		int ls = tr[p].ls, rs = tr[p].rs;
		if (ls) tr[ls].mul(lzy);
		if (rs) tr[rs].mul(lzy);
		lzy = 1;
	}
	return;
}

void Add(int x, LL v, int p)
{
	if(tr[p].is_leaf())
	{
		(tr[p].sum += v) %= MOD;
		(tr[p].dat += sorted[tr[p].l] * v) %= MOD;
		return;
	}
	int mid = tr[p].mid();
	if(x <= mid)
	{
		check(tr[p].ls, tr[p].l, mid);
		Add(x, v, tr[p].ls);
	}
	else
	{
		check(tr[p].rs, mid+1, tr[p].r);
		Add(x, v, tr[p].rs);
	}
	pushup(p);
	return;
}

int Merge(int p, int q, int l, int r, LL pmul, LL qmul)
{
	if(!p && !q) return 0;
	if(!p)
	{
		tr[q].mul(qmul);
		return q;
	}
	if(!q)
	{
		tr[p].mul(pmul);
		return p;
	}
	pushdown(p), pushdown(q);
	int mid = l + r >> 1;
	LL spr = tr[tr[p].rs].sum, sqr = tr[tr[q].rs].sum;
	tr[p].ls = Merge(
		tr[p].ls, tr[q].ls,
		l, mid,
		(pmul + sqr) % MOD, (qmul + spr) % MOD
	);
	tr[p].rs = Merge(
		tr[p].rs, tr[q].rs,
		mid + 1, r,
		pmul, qmul
	);
	pushup(p);
	return p;
}

/*---------- Dynamic Segment Tree - End ----------*/ 

LL binpow[N];
int sz[N];
void DFS(int x, int fa)
{
	sz[x] = 1;
	for (int i = head[x]; i; i = edge[i].nxt)
	{
		int y = edge[i].to;
		if (y == fa) continue;
		DFS(y, x);
		rt[x] = Merge(rt[x], rt[y], 1, n, binpow[sz[y] - 1], 0);
		sz[x] += sz[y];
	}
	(ans += binpow[max(n - sz[x] - 1, 0)] * tr[rt[x]].dat % MOD) %= MOD;
	return;
}

int main()
{
	read(n);
	for (int i = 1; i <= n; i++)
		read(raw[i]);
	for (int i = 1; i < n; i++)
	{
		int x, y; read(x), read(y);
		add(x, y), add(y, x);
	}
	Disc();
	binpow[0] = 1;
	for(int i = 1; i <= n; i++)
	{
		binpow[i] = (binpow[i - 1] << 1) % MOD;
		check(rt[i], 1, n);
		Add(disc[i], 1, rt[i]);
	}
	DFS(1, 0);
	write(ans, '\n');
	return 0;
}
posted @ 2025-05-19 16:42  Jerrycyx  阅读(65)  评论(0)    收藏  举报