线段树+扫描线，解决“静态矩阵加和+矩阵查询”问题

在试图用 CDQ 分治做这道题的时候遇到了一些麻烦，修改全部在查询之前的静态部分不会做，题解虽然还算详细，但是本人蒟蒻仍然无法理解，思考一上午，尝试过各种证明方法后，大致证明题解算法的正确性，记录在这里。

---

先看题解的说法和代码：

使用扫描线、线段树和差分离线解决静态问题：平面加之后平面求和。

扫描线的收益：问题降一维，维护一个一维线段树即可。

扫描线的代价：问题转为在线，所以扫描线只能用一次。

将修改和查询按照某个坐标轴差分成两个平面修改或平面查询（将矩形拆成两个等长对边），本文中扫描线全部按 \(y\) 轴差分且按照 \(y\) 轴坐标从小到大扫描。

为保证答案正确，差分时将询问中高度较小一边高度 \(−1\)，修改中高度较大一边高度 \(+1\)，等高度的情况先执行修改操作。

使用两次扫描线，第一次扫描时直接执行修改，在查询时将贡献乘以该查询的 \(y\) 轴坐标 \(+1\)（查询的 \(y\) 轴坐标修改后可能是 \(0\)，两次统计时线段树中的信息可能不等），同一查询先减后加。第一次扫描线的修改如果全部执行，线段树会自行清空。第二次扫描时将修改的贡献乘以其 \(y\) 轴坐标，同一查询先加后减，线段树不会清空这次扫描的修改，差分后的修改带了高度权值。

可以感性理解为第一次统计查询范围内“不完整”的矩形，第二次统计查询范围内“完整”的矩形并且去掉第一次扫描加入的多余贡献。

时间复杂度 \(O(n \log n)\)。

所给代码片段：

void scan_line_I(){
	int i=1,j=1;//i:修改 j:询问 
	while(j<=m)
		if(i<=n&&c[i].y<=q[j].y) update(1,c[i].l,c[i].r,c[i].v),i++;
		else{
			int now=query(1,q[j].l,q[j].r)*(q[j].y+1);//必须+1 
			ans[q[j].i]+=on[q[j].i] ? now:-now;
			on[q[j++].i]=1;//标记已处理 
		}
	while(i) update(1,c[i].l,c[i].r,-c[i].v),i--;//清空 
}
void scan_line_II(){
	int i=1,j=1;
	memset(on,0,sizeof(on));//取消标记 
	while(j<=m)
		if(i<=n&&c[i].y<=q[j].y) update(1,c[i].l,c[i].r,c[i].v*c[i].y),i++;
		else{
			int now=query(1,q[j].l,q[j].r);
			ans[q[j].i]+=on[q[j].i] ? -now:now;
			on[q[j++].i]=1;
		}
	//可选:清空 
}

---

以下默认坐标系竖直方向为 \(x\) 轴；正方向向下，水平方向为 \(y\) 轴，正方向向右。即 \(x\) 表示行数，\(y\) 表示列数的“OI 坐标系”。扫描线方向为 \(x\) 从小到大扫（注意与前面引用的题解不同）。

对于这个问题，采用的方法是二维类前缀和，即 \(\sum_{i=x_1}^{x_2} \sum_{j=y_1}^{y_2} a_{i,j} = \sum_{i=0}^{x_2} \sum_{j=y_1}^{y_2} a_{i,j} - \sum_{i=0}^{x_1-1} \sum_{j=y_1}^{y_2} a_{i,j}\)，也就是如图所示的总体部分减黄色部分等于绿色部分：

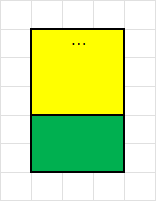
题解中给的做法第一次先减再加，第二次先加再减。实际上，第一次减、第二次加的总和为黄色部分 \(\sum_{i=1}^{x_1-1} \sum_{j=y_1}^{y_2} a_{i,j}\)；第二次加、第二次减的总和为总体部分 \(\sum_{i=1}^{x_2} \sum_{j=y_1}^{y_2} a_{i,j}\)。

两部分本质上是一样的，都是在求对于某一组 \(k,l,r\) 的 \(\sum_{i=1}^{k} \sum_{j=y_1}^{y_2} a_{i,j}\)，所以我们只需证明算法能够正确求解这个式子就可以了。

---

首先来看第一次扫描线做了什么：这个扫描线所用线段树的修改是正常的，而查询则要乘上一个倍数。

\[k \cdot \sum_{l=1}^{r} a_{k,i} \]

这个式子表达了什么含义？理解一下，其实就是假装前 \(k\) 行的都和 \(a_{k,l \sim r}\) 相同，得到的答案。但是这个假设显然是不成立的，所以第二次扫描线就是在补齐不成立导致的误差。

一个修改矩形的左右端点无关紧要，只考虑上下端点对于误差的贡献。再次运用差分思想，把一个对 \(x_1 \sim x_2\) 增加了 \(v\) 的修改拆分成两个修改：对 \(x_1 \sim +\infin\) 增加 \(v\)、对 \(x_2+1 \sim +\infin\) 增加 \(-v\)。

如此一来，问题再次简化，现在只有从某一行开始的永久性增加了。

设从第 \(x\) 行开始（\(x<k\)，否则修改不影响查询，没有意义），永久增加一个 \(v\)，那么第 \(k\) 行就一定包含了这部分 \(v\) 的贡献。然而，在第 \(x\) 行以前，这部分贡献实际上是不存在的，所以对于前面的 \(x-1\) 行，我们每一行都额外算了 \(v\) 贡献。所以第二次扫描线的修改部分要乘以一个 \((x-1)\)。（题解里面给的是第一次乘以 \(x+1\)，第二次乘以 \(x\)，和我这个写法是一样的）。

---

这样，我们证明了：一个 \(y_2\) 是 \(+\infin\) 的修改对于一个查询，是可以得到正确答案的。

因为任意一个的 \(y_2 \neq +\infin\) 修改都可以用差分拆成两个 \(y_2=+\infin\) 的修改，所以 \(\sum_{i=1}^{k} \sum_{j=y_1}^{y_2} a_{i,j}\) 也可以正确求解。

“对于某一组 \(k,l,r\) 的 \(\sum_{i=1}^{k} \sum_{j=y_1}^{y_2} a_{i,j}\)”可正确求解以后，因为矩形区域和也可以转化成这样的两个式子之差的形式，所以所以对于任意单个修改对任意单个查询，答案都是正确的

由乘法和加法的分配律和结合律，以及差分和初始状态无关而只与变化量有关的特性，各个修改对于一个查询的影响可以直接这样叠加而不会出错查询之间也互不影响，所以对于任意多个修改和任意多个查询，算法依然是正确的。

总的来说，证明过程不停地使用差分来合并和简化情况，从“多对多”转成“一对一”，从“有四个维度的任意矩形区域和”转成“有三个维度的矩形前缀和”，从“二维的临时增加”转成“一维的永久增加”，大大简化了问题。

---

我最开始的证明其实是大规模的分类讨论，勉强证明了算法正确性。本文动笔一半后，我越发觉得这种证明方法不够优雅，也不像是正常人类推出算法的思维逻辑。所以我抛弃了原先别扭的证明思路，从常见的矩形前缀和相减的方式，通过平衡误差的方式来考虑整个算法，最终不断简化情况，证明成功。这种思路更接近于人类能想到的算法逻辑，也使我受益匪浅。