2024.11.15 NOIP 模拟 - 模拟赛记录
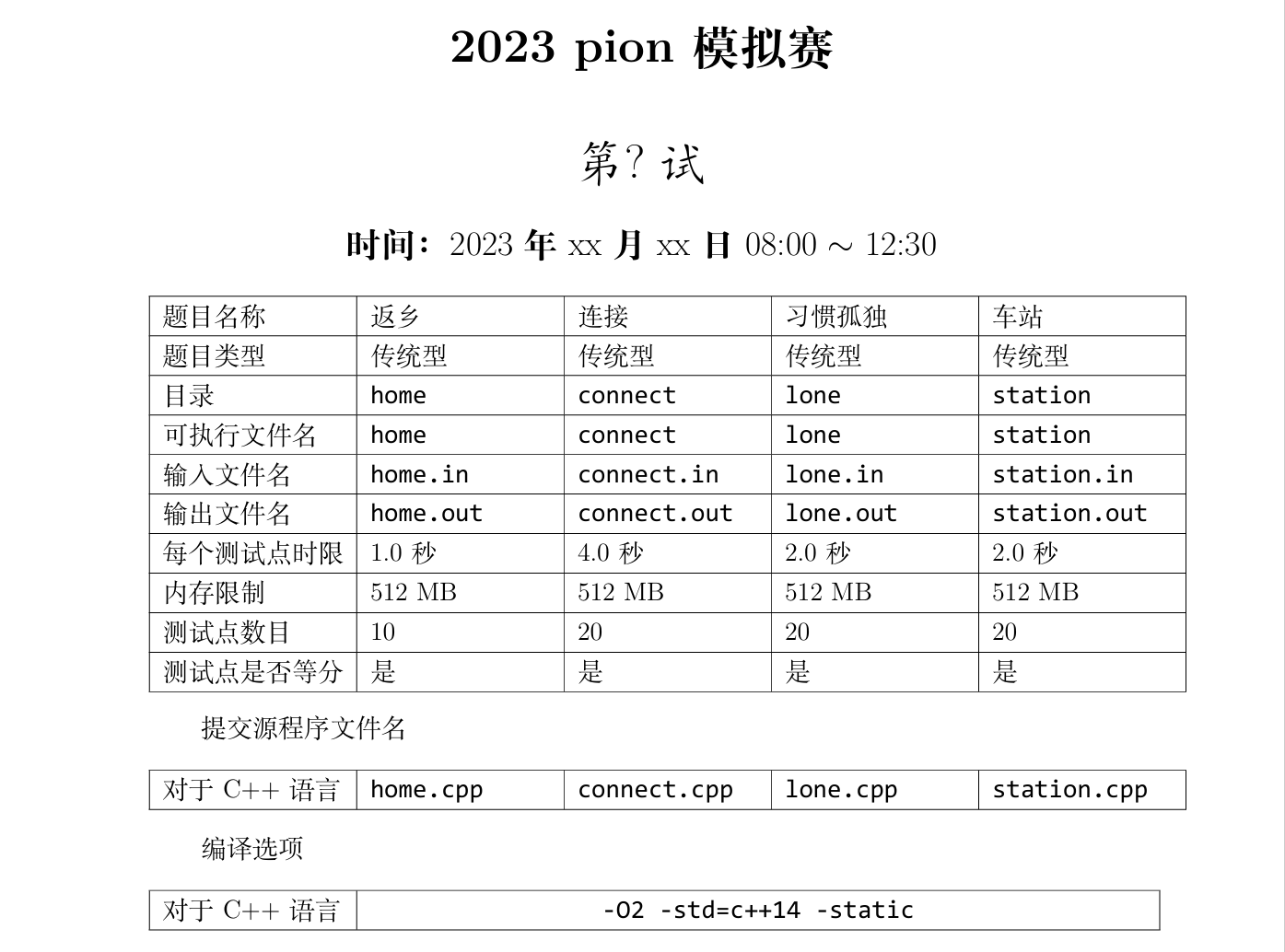
返乡(home)
不给大样例是怕我找规律出答案吗?但是我还是找到规律了。
题解说是结论题,但是这个结论即使观察小样例也很好猜(如果我是出题人就把样例打乱一下顺序)。
首先考虑只有二维偏序时的最优放置方法:
首先第一个数是不能重复的,因为一旦重复,第二个数无论怎么选,都会构成偏序;第二个数同理,也不能重复。所以最多有 \((n+1)\) 个二元组。
那么我们将 \(0 \sim n\) 全部放上去,并且将第一个数排序,试试看能不能抵满上限。
因为不能构成偏序,所以对于第二个数,后面的不能比前面的更大(这样的话,因为后面的第一个数本来就比前面的第一个数更大,两个都更大就构成偏序了),所以后面的需要是从大到小的顺序排列。
当 \(N=4\) 时,一种最优放法如下:
(如果最左侧多了一列数字,请忽略,那是代码块行号,下同)
0 4
1 3
2 2
3 1
4 0
再来考虑三维偏序的情况:
如果第一个数相同,第二三个数可以转化成上面的二维偏序形式,放法与上面所述相同。
观察样例,第一个数为 \(0\) 有两个,\(1\) 有三个,\(2\) 有两个,所以我们先放 \(1\) 试试看:
1 0 2
1 1 1
1 2 0
放了 \(1\) 以后,对于第一个数小于 \(1\) 的,后面两个数的值域需要更大才能够不被 \(1\) 开头的三元组偏序,所以我们从 \(1\) 开始放(这个观察样例也很好发现吧)。
0 1 2
0 2 1
1 0 2
1 1 1
1 2 0
而第一个数大于 \(1\) 的三元组,后面数的值域应当更小才不会偏序 \(1\) 开头的三元组,我们只能放到 \(1\):
0 1 2
0 2 1
1 0 2
1 1 1
1 2 0
2 0 1
2 1 0
所以规律即为:从中间开始放数,前面的三元组后两个数的最小值逐渐增加,后面的三元组后两个数的最大值逐渐减小。
正确性严格证明不会,但是可以感性理解一下:第一个数递增或递减的时候,所可以构成的三元组数量每次都一定要减一的,把最开始三元组最多的那一个放在正中间可以让所减的值最小。
int n;
struct Triple{
int x,y,z;
}ans[300000];
int tot=0;
int main()
{
freopen("home.in","r",stdin);
freopen("home.out","w",stdout);
read(n);
for(int i=0;i<=n>>1;i++)
{
int s=(n>>1)-i; //start point
for(int j=s;j<=n;j++)
ans[++tot]={i,j,s+n-j};
}
for(int i=(n>>1)+1;i<=n;i++)
{
int t=n-(i-(n>>1)); //end point
for(int j=0;j<=t;j++)
ans[++tot]={i,j,0+t-j};
}
write(tot,'\n');
for(int i=1;i<=tot;i++)
write(ans[i].x,' '),write(ans[i].y,' '),write(ans[i].z,'\n');
return 0;
}
连接(connect)
好家伙,数学证明题。
结论 \(1\):所截区间的一个端点在钢管交界处。
证明:
-
当所截不足一整根钢管时,截的时这根钢管的哪一部分无关紧要,端点在交界处的截法自然也是最优解。
-
当所截超过一根钢管时,根据最左右两侧钢管的密度,又分两种情况:
- 左右两侧钢管密度相同,所截的左右端点可以在不超过这两根钢管的前提下任意滑动,端点在交界处的截法也是最优解之一。
- 左右两侧钢管密度不同,那么一定有密度较大的那一根,把两端点同时向密度大的钢管移动直到某一侧端点抵达钢管交界(不一定是最近的交界)而无法再移(再移答案会更劣),答案只会更优。
综上所述,最优解所截区间至少有一个端点在钢管交界处。
结论 \(2\):答案区间可能有以下几种情况:
- 质量刚好为 \(L\) 或 \(R\),此时因为质量上限或下限限制无法再截更多。
- 所截区间两个端点均在钢管交界处,此时因为外侧钢管密度过低,再多截会使总密度降低。
正确性显然。
所以就有一个半正解做法:
枚举右端点 \(i\),找到如果取满质量 \(R\),左端点可以取最左位置 \(left\) 和如果取满质量 \(L\),左端点可以取的最右位置 \(right\)。
刚好取质量 \(L\) 和 \(R\) 的答案很好算,就是式子有点长,分别是:
对于取到交界处的答案,假设一直取完到第 \(j\) 根钢管,那么此时的答案就是:
至于枚举左端点,把输入序列翻转一下就可以了,不用再写一遍。
对于求 \(left\) 和 \(right\),因为质量的增加具有单调性,所以可以用二分或双指针(实际上是三指针)来求,下面提供两种方法的参考代码(均为 \(50\) 分):
点击查看代码 · 二分
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=3e5+5;
int n;
double L,R;
double s[N],p[N],m[N];
double ssum[N],msum[N];
double ans;
void Prework()
{
for(int i=1;i<=n;i++)
{
m[i]=s[i]*p[i];
msum[i]=msum[i-1]+m[i];
ssum[i]=ssum[i-1]+s[i];
}
return;
}
void Solve()
{
for(int i=1;i<=n;i++)
{
int l=0,r=i+1; //l[left,i]>R; r[left+1,i]<=R
while(l+1<r)
{
int mid=l+r>>1;
if(msum[i]-msum[mid-1]<=R) r=mid;
else l=mid;
}
int left=l;
l=0,r=i+1; //l[right,i]>=L; r[right+1,i]<L
while(l+1<r)
{
int mid=l+r>>1;
if(msum[i]-msum[mid-1]>=L) l=mid;
else r=mid;
}
int right=l;
double pre_ans_l= R / ((ssum[i]-ssum[left]) + (R-(msum[i]-msum[left]))/p[left]);
double pre_ans_r= L / ((ssum[i]-ssum[right]) + (L-(msum[i]-msum[right]))/p[right]);
ans=max({ans,pre_ans_l,pre_ans_r});
for(int j=left+1;j<=right;j++)
ans=max(ans,(msum[i]-msum[j-1])/(ssum[i]-ssum[j-1]));
}
return;
}
int main()
{
freopen("connect.in","r",stdin);
freopen("connect.out","w",stdout);
scanf("%d%lf%lf",&n,&L,&R);
for(int i=1;i<=n;i++) scanf("%lf",&s[i]);
for(int i=1;i<=n;i++) scanf("%lf",&p[i]);
Prework(); Solve();
reverse(s+1,s+n+1),reverse(p+1,p+n+1);
Prework(); Solve();
printf("%.15lf",ans);
return 0;
}
点击查看代码 · 双指针
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=3e5+5;
int n;
double L,R;
double s[N],p[N],m[N];
double ssum[N],msum[N];
double q[N]; int head,tail;
double ans;
void Prework()
{
for(int i=1;i<=n;i++)
{
m[i]=s[i]*p[i];
msum[i]=msum[i-1]+m[i];
ssum[i]=ssum[i-1]+s[i];
}
return;
}
void Solve()
{
int left=0,right=0;
for(int i=1;i<=n;i++)
{
while(left<=i && msum[i]-msum[left+1-1]>R) left++;
while(right<=i && msum[i]-msum[right+1-1]>=L) right++;
double pre_ans_l= R / ((ssum[i]-ssum[left]) + (R-(msum[i]-msum[left]))/p[left]);
double pre_ans_r= L / ((ssum[i]-ssum[right]) + (L-(msum[i]-msum[right]))/p[right]);
ans=max({ans,pre_ans_l,pre_ans_r});
double tmp=0;
if(n<=100000)
{
for(int j=left+1;j<=right;j++)
ans=max(ans,(msum[i]-msum[j-1])/(ssum[i]-ssum[j-1]));
}
else
{
for(int j=left+1;j<=right;j++)
{
double val=(msum[i]-msum[j-1])/(ssum[i]-ssum[j-1]);
if(val>tmp)
{
tmp=val;
}
}
}
}
return;
}
int main()
{
freopen("connect.in","r",stdin);
freopen("connect.out","w",stdout);
scanf("%d%lf%lf",&n,&L,&R);
for(int i=1;i<=n;i++) scanf("%lf",&s[i]);
for(int i=1;i<=n;i++) scanf("%lf",&p[i]);
Prework(); Solve();
reverse(s+1,s+n+1),reverse(p+1,p+n+1);
Prework(); Solve();
printf("%.15lf",ans);
return 0;
}
结论 \(3\):如果取钢管区间 \(a \sim i\) 优于取钢管区间 \(b \sim i\) 更优,那么取钢管 \(a \sim i+1\) 仍然优于取钢管 \(b \sim i+1\)。
不会证明,这是官方题解的证明,虽然我也没看懂:

所以在前面更劣的左端点区间在后面一定不会优,这个可以用单调队列维护。
我的写法是基于双(三)指针写法的,\(left\) 右移的时候,合法区间 \([left,right]\) 左边少了一个 \(left\),这时候判断一下 \(left\) 是否是单调队列队头(我的代码队头在左,队尾在右),如果是就需要弹出队头,因为此时队头已经不符合条件了。
\(right\) 右移的时候,相当于合法区间 \([left,right]\) 右边扩展了一个 \(right\),这个时候就需要通过公式 \(\frac{sum_m(j,i)}{sum_l(j,i)}\) 计算出 \(right\) 对于 \(i\) 的答案再与队尾存的可行端点所得答案进行比较,若当前答案更大就弹出队尾直到队尾所得大于当前所得或队空,然后把当前所得加进去(其实就是单调队列滑动窗口的过程)。
注意右移 \(right\) 需要先于右移 \(left\),因为新加入的值可能符合 \(right\) 的要求而不符合 \(left\) 的要求,后进行 \(left\) 右移就可以处理掉这些值。
然后此时,如果直接只取队头来更新答案,所得答案不一定正确(\(95\) 分),但是如果取了队头和队头的后一个数就可以 AC 了。但是这样做依然是错的,仍然能被 Hack 掉,能过只是因为数据水(我随机数据对拍大约 \(60\) 组数据就可以出一组 Hack)。
所以正解是将此时队列中所有的可行端点都用来更新答案,但这又造成了一个新问题,这个稍后再讲。
参考代码 (不得不说官方给的代码是真的丑,还是我的更好看):
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=3e5+5;
int n;
double L,R;
double s[N],p[N],m[N];
double ssum[N],msum[N];
double ans;
void Prework()
{
for(int i=1;i<=n;i++)
{
m[i]=s[i]*p[i];
msum[i]=msum[i-1]+m[i];
ssum[i]=ssum[i-1]+s[i];
}
return;
}
double calc(int l,int r)
{
return (msum[r]-msum[l-1])/(ssum[r]-ssum[l-1]);
}
int q[N];
void Solve()
{
int head=1,tail=0; //!!!
int left=0,right=0;
for(int i=1;i<=n;i++)
{
while(right<=i && msum[i]-msum[right+1-1]>=L)
{
right++;
double val=calc(right,i);
while(head<=tail && val>=calc(q[tail],i)) q[tail--]=0;
q[++tail]=right;
}
while(left<=i && msum[i]-msum[left+1-1]>R)
{
if(q[head]==left+1) q[head++]=0;
left++;
}
double pre_ans_l= R / ((ssum[i]-ssum[left]) + (R-(msum[i]-msum[left]))/p[left]);
double pre_ans_r= L / ((ssum[i]-ssum[right]) + (L-(msum[i]-msum[right]))/p[right]);
ans=max({ans,pre_ans_l,pre_ans_r});
for(int j=head;j<=tail;j++)
ans=max(ans,calc(q[j],i));
}
return;
}
int main()
{
freopen("connect.in","r",stdin);
freopen("connect.out","w ",stdout);
scanf("%d%lf%lf",&n,&L,&R);
for(int i=1;i<=n;i++) scanf("%lf",&s[i]);
for(int i=1;i<=n;i++) scanf("%lf",&p[i]);
Prework(); Solve();
reverse(s+1,s+n+1),reverse(p+1,p+n+1);
Prework(); Solve();
printf("%.15lf",ans);
return 0;
}
刚才提到的问题就是,这个算法的时间复杂度是不完善的。根据题解描述,在随机数据下其时间复杂度接近 \(O(n \log n)\),但是通过特殊构造的数据可以让它无法或很少能够弹出单调队列,可以卡成 \(O(n^2)\)。
具体来说,如果让 \(L\) 极小而 \(R\) 极大,并且让所有的 \(l\) 都差不多大,让 \(p\) 从大到小排列,就可以让每次的解都能比上一次更劣从而无法弹出单调队列。
附上这样的数据生成器和一份 Hack 数据:点击下载压缩包。
然而这并不能卡掉验题人题解。
这样,刚才的 \(99\%\) 正确解法(只取队列前两个)就发挥它的作用了,它是标准的 \(O(N)\) 算法,如果怕错还可以再多取几个(我直接取了 \(100\) 个,然后 \(10000+\) 组极限数据都 Hack 不掉),这样就是 \(99.99\dots99 \%\) 解法了,几乎卡不掉。
代码上,只需要将 for(int j=head;j<=tail;j++) 改成 for(int j=head;j<=min(head+100,tail);j++) 即可。
习惯孤独(lone)
暴力爽题,可惜我低估了我暴力代码的效率加了个 if(n>1000) write(0,'\n'); 从而 \(70 \rightarrow 30\) Pts。
接下来是 \(70+\) 分暴力做法:
首先 DFS 一遍处理出每个节点的子树大小 \(sz\) 和它的父节点和,并且只从父节点向子节点连边来重建一棵树(主要是为了方便后续处理,不重建也行)。
然后直接在新建的树上跑 DFS,这个 DFS 同时完成两个操作:如果在某处切了一刀,那么它是在枚举所切位置;如果没有切成功,那么它是在遍历找可以切的位置。
(其实我现在看我之前写的代码也觉得挺神奇的,这种写法也不知道叫什么,也不知道当时我是怎么写出来的。)
然后判断某条边 \(x \rightarrow y\) 是否能切,切边有一下两种可能:
- 切除上面,保留子树 \(subtree(y)\)
- 切除子树 \(subtree(y)\),保留其它部分
要实现以上操作,需要在 DFS 的时候记录当前节点编号 \(x\),当前遍历到序列 \(a\) 的位置 \(p\),当前工作子树的根节点编号 \(root\),在切除子树时,从 \(root\) 到 \(x\) 的所有点的子树大小都要减少 \(sz_y\)。
说的不是很清楚,但是 Talk is cheap, Show me your code!
#include<cstdio>
using namespace std;
namespace IO{
template<typename TYPE> void read(TYPE &x)
{
x=0; bool neg=false; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')neg=true;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^'0');ch=getchar();}
if(neg){x=-x;} return;
}
template<typename TYPE> void write(TYPE x)
{
if(!x){putchar('0');return;} if(x<0){putchar('-');x=-x;}
static int sta[55];int statop=0; while(x){sta[++statop]=x%10;x/=10;}
while(statop){putchar('0'+sta[statop--]);} return;
}
template<typename TYPE> void write(TYPE x,char ch){write(x);putchar(ch);return;}
} using namespace IO;
const int N=5005,K=10,P=998244353;
int n,k,a[K];
long long ans=0;
struct{
struct Allan{
int to,nxt;
bool unable;
}edge[N<<1];
int idx,head[N];
inline void add(int x,int y)
{
edge[++idx]={y,head[x],false};
head[x]=idx;
return;
}
}raw,tree;
int fa[N],sz[N];
namespace Prework{
void DFS(int x)
{
sz[x]=1;
for(int i=raw.head[x];i;i=raw.edge[i].nxt)
{
int y=raw.edge[i].to;
if(sz[y]) continue;
tree.add(x,y);
fa[y]=x;
DFS(y);
sz[x]+=sz[y];
}
return;
}
}
namespace Solve{
void modify(int x,int tgt,int z)
{
while(x!=tgt)
{
sz[x]+=z;
x=fa[x];
}
sz[tgt]+=z;
return;
}
void DFS(int x,int p,int root)
{
if(p>k) {ans++; return;}
if(sz[root]<=a[p]) return;
for(int i=tree.head[x];i;i=tree.edge[i].nxt)
{
if(tree.edge[i].unable) continue;
int y=tree.edge[i].to;
if(sz[y]==a[p]) //保留下面,砍掉上面
{
tree.edge[i].unable=true;
DFS(y,p+1,y);
tree.edge[i].unable=false;
}
if(sz[root]-sz[y]==a[p]) //保留上面,砍掉下面
{
tree.edge[i].unable=true;
modify(x,root,-sz[y]);
DFS(root,p+1,root);
tree.edge[i].unable=false;
modify(x,root,sz[y]);
}
DFS(y,p,root);
}
return;
}
}
int main()
{
freopen("lone.in","r",stdin);
freopen("lone.out","w",stdout);
read(n);
for(int i=1;i<n;i++)
{
int x,y; read(x),read(y);
raw.add(x,y),raw.add(y,x);
}
Prework::DFS(1);
read(k);
for(int i=1;i<=k;i++)
read(a[i]);
Solve::DFS(1,1,1);
write(ans,'\n');
return 0;
}
车站(station)
不会做,输出了个 \(-1\),竟然一分都没有。(话说没有 \(-1\) 的数据不会放掉不判无解的错解吗?)
以下代码可骗 \(10\) 分(特殊性质):
点击查看代码
#include<cstdio>
#include<algorithm>
#define int long long
using namespace std;
#ifndef JC_LOCAL
const int SIZE=1<<20; char buf[SIZE],*p1=buf,*p2=buf;
#define getchar() ((p1==p2&&(p2=(p1=buf)+fread(buf,1,SIZE,stdin),p1==p2))?EOF:*p1++)
#endif
template<typename TYPE> void read(TYPE &x)
{
x=0; bool neg=false; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')neg=true;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+(ch^'0');ch=getchar();}
if(neg){x=-x;} return;
}
const int N=2e5+5,M=2e5+5,P=998244353;
int n,m,k;
struct Allan{
int to,nxt;
int val;
}edge[M];
int head[N],idx;
inline void add(int x,int y,int z)
{
edge[++idx]={y,head[x],z};
head[x]=idx;
}
int quick_pow(long long x,int y)
{
long long res=1;
while(y)
{
if(y&1) res=res*x%P;
x=x*x%P;
y>>=1;
}
return res;
}
signed main()
{
freopen("station.in","r",stdin);
freopen("station.out","w",stdout);
read(n),read(m),read(k);
for(int i=1;i<=m;i++)
{
int x,y,z;
read(x),read(y),read(z);
add(x,y,z);
}
if(k==n) printf("0\n");
else if(k==n-1)
{
long long sum=0;
for(int x=1;x<=n;x++)
{
int minval=0x3f3f3f3f;
for(int i=head[x];i;i=edge[i].nxt)
minval=min(minval,edge[i].val);
sum=(sum+minval)%P;
}
printf("%lld\n",sum*quick_pow(n,P-2)%P);
}
else printf("-1\n");
return 0;
}
本文采用 「CC-BY-NC 4.0」 创作共享协议,转载请注明作者及出处,禁止商业使用。
作者:Jerrycyx,原文链接:https://www.cnblogs.com/jerrycyx/p/18548252


 浙公网安备 33010602011771号
浙公网安备 33010602011771号