2024.11.12 NOIP模拟 - 模拟赛记录

Preface

（以下为吐槽内容，可以跳过）

一套烂题。

T1 一眼搬的 CF（赛后十秒就找到原题了），只搬 idea 就算了，根本不设置部分分，大样例给的更是一坨（数据范围给的 \(10^{15}\)，1 2 10 72 121 算什么大样例？），甚至最后的题解都是直接复制的洛谷。

T2 稍好，除了实数运算稍微恶心一点，其它都没什么。

T3 又是一大坨，不给 SPJ 都无所谓（虽然我严重怀疑它的 SPJ 有问题 确实有问题），但是题解上说测试点 \(1,2\)“随便暴力”是什么鬼？暴力的时间复杂度只与 \(m\) 有关，\(n \le 5\) 的数据更是不伦不类，虽然这两个点的 \(m\) 确实都很小，但是题面上压根没提。这道题的第 \(5\) 个测试点更是部分分 std 都过不去（一共就三行代码能怎么错？）；第 \(2,4\) 个点也莫名其妙地能够把纯暴力卡 WA，这套数据大概率不是 SPJ 写错了，就是数据生成器有问题 破案了，就是 SPJ 的问题，SPJ 改好以后能正常拿分。

T4 也爽，题面直接是错的。原题面是这样的：

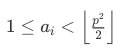
image

一到题解上，欸，它就变成这样啦：

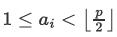
image

而后面的一条数据范围是解题所必须的，连这都能牛头不对马嘴，我也无话可说。

吐槽完毕，进入正题。

总体难度一般，个人感觉难度在黄（绿）绿蓝（紫）绿（黄）左右，但是恶心程度拉满，我的评价是：黑黑黑黑。

T1 做的太着急了，赶着去做后面，导致挂掉，其实 T1 可以做慢点（\(1.5\) h 内都是正常时间）。

并且这次策略不佳。总结一下，对我来说正确的策略应当是：【已移动至《技巧 + 注意事项》】

基于1的算术（add）

这是 Codeforces 上的原题（440C）。虽说大样例依托答辩，但是我用数学方法写了一遍以后也太自信了一点，在不确定算法正确性的前提下随便测了几组 Hack 没发现错误以后就直接换题了。

以后遇到这样不确定正确性的算法，一定要打暴力对拍一下，尤其是在 T1 挂的分是承受不起的。

一定要打暴力和对拍，这花不了你多长时间。——洛谷某用户

比如这次直接挂 \(50\) 分，\(225 \rightarrow 175\)，爽飞。

赛后补题参照这篇题解，后面可能我自己也会写一篇题解。

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define LL long long
using namespace std;

LL n;
LL zero[20],one[20];
void Prework()
{
	zero[1]=one[1]=1;
	for(int i=2;i<=16;i++)
	{
		zero[i]=zero[i-1]*10;
		one[i]=one[i-1]*10+1;
	}
	return;
}
int ans=0x3f3f3f3f;
void DFS(LL x,int pos,int now)
{
	if(now>ans) return;
	if(x==0){ans=min(ans,now);return;}
	if(x<0) x=-x;
	if(x/zero[pos]==0){DFS(x,pos-1,now);return;}
	
	LL r1=x; int add1=0;
	while(r1>=zero[pos])
	{
		r1-=one[pos];
		add1+=pos;
	}
	DFS(r1,pos-1,now+add1);
	
	LL r2=one[pos+1]-x; int add2=pos+1;
	while(r2>=zero[pos])
	{
		r2-=one[pos];
		add2+=pos;
	}
	DFS(r2,pos-1,now+add2);
	
	return;
}

int main()
{
	freopen("add.in","r",stdin);
	freopen("add.out","w",stdout);
	
	scanf("%lld",&n);
	Prework();
	DFS(n,15,0);
	printf("%d\n",ans);
	return 0;
}

逃离（car）

目测绿的样子（而且不是上位绿），算是结论题。

image

做题时思维没能打开，只想到某辆车离开与前一辆车有关，而没想到一路推过去，前一辆车又与更前面的车相关，进而某一辆车是否能离开与前面所有车都有关。

但是有了这个结论还不够，还要想到把这个结论反过来：当前车会影响后面所有车，只有当到达某个位置的时候才不会影响后面车的离开。

最后优先队列处理最大值什么的就都很好想了。

const int N=3e5+5,M=3e5+5;
int n,t,m,k;
struct Rain{
	long long l,r,v;
}car[N];

#define PDI pair<double,int>
priority_queue<PDI> pq;
long long sum[N];

bool cmp(Rain x,Rain y){return x.l<y.l;}
int main()
{
	freopen("car.in","r",stdin);
	freopen("car.out","w",stdout);
	
	read(n),read(t),read(m),read(k);
	for(int i=1;i<=n;i++)
		read(car[i].l),read(car[i].r),read(car[i].v);
	sort(car+1,car+n+1,cmp);
	for(int i=1;i<=n;i++)
	{
		sum[i]=sum[i-1]+car[i].r-car[i].l;
		double need_ti=1.0*(sum[i-1]+t-car[i].l)/car[i].v;
		pq.push({need_ti,i});
	}
	for(int i=1;i<=m;i++)
	{
		PDI x=pq.top(); pq.pop();
		int p=x.second;
		car[p].v+=k;
		double need_ti=1.0*(sum[p-1]+t-car[p].l)/car[p].v;
		pq.push({need_ti,p});
	}
	printf("%.3lf\n",pq.top().first);
	return 0;
}

南斯拉夫（yugo）

恶心，等先把 SPJ 错误的问题解决了再说吧。 已经解决了。

官方题解：

image

体感难度蓝左右，思路就是题解思路，但是我的写法感觉更清晰明了而且更好调试。

建立三个图，分别存原图（双向边），树（双向边），答案图（单向边），在原图上跑一遍得到树和部分答案图，再在树上跑一遍得到另一部分答案图。

最后遍历答案图内所有边，根据其指向和顶点入度来存入答案。

合理使用 namespace 能够大大减少变量混用出 BUG 的概率。

分成几段可能更好看一点：

变量定义 + 存图 
const int N=1e6+5,M=1e6+5;
const char NO[105]="Yugoslavia is unstable!";
int T,n,m;
pair<int,int> a[N];
bool have_ans=true;

struct Graph{
	struct Allan{
		int to,nxt;
		int id;
	}edge[M<<1];
	int head[N],idx,deg[N];
	inline void add(int x,int y,int id)
	{
		deg[y]++;
		edge[++idx]={y,head[x],id};
		head[x]=idx;
		return;
	}
}raw,tree,ans;
inline int rev(int id){return id&1?id+1:id-1;}
int alr[N];
遍历原图，判断合法性，得到树和部分答案 
namespace Build_tree{

bool in_tree[M<<1],vst[N];
bool added[M<<1];
int edge_cnt;
void DFS(int x)
{
	vst[x]=true;
	for(int i=raw.head[x];i;i=raw.edge[i].nxt)
	{
		int y=raw.edge[i].to,id=raw.edge[i].id;
		edge_cnt++;
		if(vst[y])
		{
			if(!in_tree[i]&&!added[i]) //非树边
			{
				added[i]=added[rev(i)]=true;
				ans.add(x,y,id);
			}
		}
		else //新树边
		{
			in_tree[i]=in_tree[rev(i)]=true;
			tree.add(x,y,id),tree.add(y,x,id);
			DFS(y);
		}
	}
	return;
}

void Process_all()
{
	for(int i=1;i<=n;i++)
		if(!vst[i])
		{
			edge_cnt=0;
			DFS(i);
			if((edge_cnt>>1)&1)
			{
				have_ans=false;
				break;
			}
		}
	return;
}

} //namespace Build_tree
遍历树，获取树边方向得到另一部分答案 
namespace Set_direction{

bool vst[N];
void DFS(int x)
{
	vst[x]=true;
	for(int i=tree.head[x];i;i=tree.edge[i].nxt)
	{
		int y=tree.edge[i].to,id=tree.edge[i].id;
		if(vst[y]) continue;
		DFS(y);
		if(ans.deg[y]&1) ans.add(x,y,id);
		else ans.add(y,x,id);
	}
	return;
}
void Process_all()
{
	for(int i=1;i<=n;i++)
		if(!vst[i]) DFS(i);
	return;
}

} //namespace Set_dirction
将答案图转化成输出要求的形式 
int ans_output[N];
void Merge_answer()
{
	for(int i=1;i<=ans.idx;i++)
	{
		int y=ans.edge[i].to,id=ans.edge[i].id;
		if(y==a[id].first) //left
		{
			if(++alr[y]<=ans.deg[y]>>1) ans_output[id]=1;
			else ans_output[id]=3;
		}
		else //right
		{
			if(++alr[y]<=ans.deg[y]>>1) ans_output[id]=2;
			else ans_output[id]=4;
		}
	}
	return;
}
主函数 
int main()
{
	freopen("yugo.in","r",stdin);
	freopen("yugo.out","w",stdout);
	
	read(T),read(n),read(m);
	for(int i=1;i<=m;i++)
	{
		read(a[i].first),read(a[i].second);
		raw.add(a[i].first,a[i].second,i);
		raw.add(a[i].second,a[i].first,i);
	}
	Build_tree::Process_all();
	if(have_ans)
	{
		Set_direction::Process_all();
		Merge_answer();
		for(int i=1;i<=m;i++)
			write(ans_output[i],' ');
	}
	else puts(NO);
	return 0;
}

完整代码：

#include<cstdio>
#include<algorithm>
using namespace std;

namespace IO{
template<typename TYPE> void read(TYPE &x)
{
	x=0; bool neg=false; char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')neg=true;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^'0');ch=getchar();}
	if(neg){x=-x;} return;
}
template<typename TYPE> void write(TYPE x)
{
	if(!x){putchar('0');return;} if(x<0){putchar('-');x=-x;}
	static int sta[55];int statop=0; while(x){sta[++statop]=x%10;x/=10;}
	while(statop){putchar('0'+sta[statop--]);} return;
}
template<typename TYPE> void write(TYPE x,char ch){write(x);putchar(ch);return;}
} using namespace IO;

const int N=1e6+5,M=1e6+5;
const char NO[105]="Yugoslavia is unstable!";
int T,n,m;
pair<int,int> a[N];
bool have_ans=true;

struct Graph{
	struct Allan{
		int to,nxt;
		int id;
	}edge[M<<1];
	int head[N],idx,deg[N];
	inline void add(int x,int y,int id)
	{
		deg[y]++;
		edge[++idx]={y,head[x],id};
		head[x]=idx;
		return;
	}
}raw,tree,ans;
inline int rev(int id){return id&1?id+1:id-1;}
int alr[N];

namespace Build_tree{

bool in_tree[M<<1],vst[N];
bool added[M<<1];
int edge_cnt;
void DFS(int x)
{
	vst[x]=true;
	for(int i=raw.head[x];i;i=raw.edge[i].nxt)
	{
		int y=raw.edge[i].to,id=raw.edge[i].id;
		edge_cnt++;
		if(vst[y])
		{
			if(!in_tree[i]&&!added[i]) //非树边
			{
				added[i]=added[rev(i)]=true;
				ans.add(x,y,id);
			}
		}
		else //新树边
		{
			in_tree[i]=in_tree[rev(i)]=true;
			tree.add(x,y,id),tree.add(y,x,id);
			DFS(y);
		}
	}
	return;
}

void Process_all()
{
	for(int i=1;i<=n;i++)
		if(!vst[i])
		{
			edge_cnt=0;
			DFS(i);
			if((edge_cnt>>1)&1)
			{
				have_ans=false;
				break;
			}
		}
	return;
}

} //namespace Build_tree

namespace Set_direction{

bool vst[N];
void DFS(int x)
{
	vst[x]=true;
	for(int i=tree.head[x];i;i=tree.edge[i].nxt)
	{
		int y=tree.edge[i].to,id=tree.edge[i].id;
		if(vst[y]) continue;
		DFS(y);
		if(ans.deg[y]&1) ans.add(x,y,id);
		else ans.add(y,x,id);
	}
	return;
}
void Process_all()
{
	for(int i=1;i<=n;i++)
		if(!vst[i]) DFS(i);
	return;
}

} //namespace Set_dirction

int ans_output[N];
void Merge_answer()
{
	for(int i=1;i<=ans.idx;i++)
	{
		int y=ans.edge[i].to,id=ans.edge[i].id;
		if(y==a[id].first) //left
		{
			if(++alr[y]<=ans.deg[y]>>1) ans_output[id]=1;
			else ans_output[id]=3;
		}
		else //right
		{
			if(++alr[y]<=ans.deg[y]>>1) ans_output[id]=2;
			else ans_output[id]=4;
		}
	}
	return;
}

namespace Debug{

void human_readable()
{
	printf("%d\n",ans.idx);
	for(int i=1;i<=m;i++)
	{
		int pos=0; bool type=false;
		if(ans_output[i]==1) pos=a[i].first,type=true;
		if(ans_output[i]==2) pos=a[i].second,type=true;
		if(ans_output[i]==3) pos=a[i].first,type=false;
		if(ans_output[i]==4) pos=a[i].second,type=false;
		printf("%d: %d%s\n",i,pos,type?"++":"--");
	}
	return;
}

}

int main()
{
	freopen("yugo.in","r",stdin);
	freopen("yugo.out","w",stdout);
	
	read(T),read(n),read(m);
	for(int i=1;i<=m;i++)
	{
		read(a[i].first),read(a[i].second);
		raw.add(a[i].first,a[i].second,i);
		raw.add(a[i].second,a[i].first,i);
	}
	Build_tree::Process_all();
	if(have_ans)
	{
		Set_direction::Process_all();
		Merge_answer();
		for(int i=1;i<=m;i++)
			write(ans_output[i],' ');
	}
	else puts(NO);
	return 0;
}

数数（count）

好家伙，数据范围都标错了，如果数据范围是对的的话其实还蛮简单的（可惜它没对），难度绿左右，主要就是考了一点数学能力。

这种题的经典套路就是要将式子左右两边转化成各只有一个变量，本题中最重要的两步就是设 \(x=a_i+1\) 和左右两边同时乘以 \((x+y)\)，而后面的那一步因为数据范围错误导致无法保证 \(x+y \neq p\) 而无法进行。

另外三次方差因式分解公式也需要牢记：\(x^3 \pm y^3 = (x \pm y)(x^2 \mp xy +y^2)\)。

官方题解：

image

const int N=5e5+5;
int n,p;
long long a[N];
unordered_map<int,int> mpx,mpy;

#define cube(x) ((__int128)(x)*(x)*(x))
#define sqr(x) ((__int128)(x)*(x))
#define mod(x) (((x)%p+p)%p)
int main()
{
	freopen("count.in","r",stdin);
	freopen("count.out","w",stdout);
	
	read(n),read(p);
	long long ans=0;
	for(int i=1;i<=n;i++)
	{
		read(a[i]);
		int x=mod(cube(a[i]+1)-sqr(a[i]+1));
		int y=mod(-cube(a[i])-sqr(a[i]));
		ans+=mpy[x]; mpy[y]++;
		ans+=mpx[y]; mpx[x]++;
	}
	write(ans,'\n');
	return 0;
}
posted @ 2024-11-12 16:54  Jerrycyx  阅读(113)  评论(0)    收藏  举报