力扣 每日一题 877. 石子游戏

今天是一个中等题，经典的博弈游戏，之前做过，今天再来回顾一下。

亚历克斯和李用几堆石子在做游戏。偶数堆石子排成一行，每堆都有正整数颗石子 piles[i] 。

游戏以谁手中的石子最多来决出胜负。石子的总数是奇数，所以没有平局。

亚历克斯和李轮流进行，亚历克斯先开始。 每回合，玩家从行的开始或结束处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止，此时手中石子最多的玩家获胜。

假设亚历克斯和李都发挥出最佳水平，当亚历克斯赢得比赛时返回 true ，当李赢得比赛时返回 false 。

示例：

输入：[5,3,4,5]
输出：true
解释：
亚历克斯先开始，只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗，这一行就变成了 [3,4,5] 。
如果李拿走前 3 颗，那么剩下的是 [4,5]，亚历克斯拿走后 5 颗赢得 10 分。
如果李拿走后 5 颗，那么剩下的是 [3,4]，亚历克斯拿走后 4 颗赢得 9 分。
这表明，取前 5 颗石子对亚历克斯来说是一个胜利的举动，所以我们返回 true 。

之前做过的朋友应该有印象，这道题啥也不管，只要看到偶数，就直接返回true即可，看到解析的时候，有种恍然大明白的感觉，所以印象深刻。能直接返回true的原因是可将石子按下标分为奇数堆和偶数堆，根据题意，这两个肯定有一个是稍大些的，先手能确定他要拿的是奇数堆还是偶数堆，所以先手总能获胜。

刷题不投机，不取巧，用自己最能想到的方式来做，将来面试时才不至于卡秃噜皮，所以还是要分析一番，写出自己的代码。

根据题意，先手第一次能拿到的最大数量应该Math.max(pile[0]+f(1,n-1),pile[n-1]+f(0,n-2))，推导出一般化的公式，即f(i,j)=Math.max(piles[i]+f(i+1,j-1),piles[j]+f(i,j-1))，当前的先手是上一把的后手，所以取得是上一把后手得最大值，所以同时需要存下后手得到得值。初始化情况下f(i,i)=piles[i]。

根据上述分析，开一个三维数组，计算方向是斜着，如下图所示。

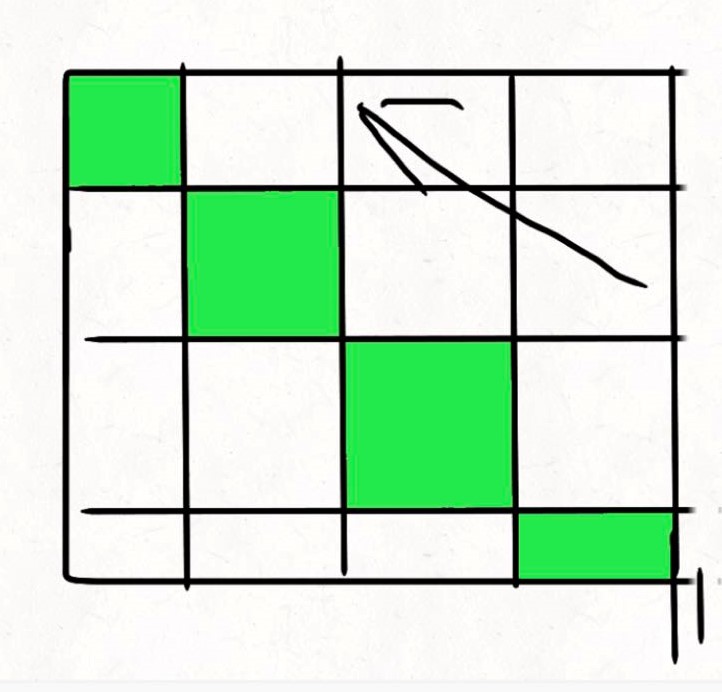
基于上述分析，写出如下代码。

 public boolean stoneGame(int[] piles) {
        int n = piles.length;
        int[][][] dp = new int[n][n][2];
        for(int i =0;i<n;i++){
            dp[i][i][0]=piles[i];
        }
        for(int slash = 1;slash<n;slash++){
            for(int point = slash;point<n;point++){
                int i = n-1-point;
                int j = i+slash;
                if(piles[i]+dp[i+1][j][1]>piles[j]+dp[i][j-1][1]){
                    dp[i][j][0]=piles[i]+dp[i+1][j][1];
                    dp[i][j][1]=dp[i+1][j][0];
                }else{
                    dp[i][j][0]=piles[j]+dp[i][j-1][1];
                    dp[i][j][1]=dp[i][j-1][0];
                }
            }
        }
        return dp[0][n-1][0]>dp[0][n-1][1];
    }

题解中可以不用记住后手得分，有兴趣可以看下。