平衡二叉树
1、什么是平衡二叉树
平衡因子(Balance Factor)
简称BF:BF(T) = h(l) - h(r),其中 h(l)和 h(r)分别是T的左、右子树的高度。
平衡二叉树(Balance Binary Tree)(AVL树)
空树,或者任一节点左、右子树的高度绝对值不超过1,|BF(T)|<=1。本质是一颗改进后的二叉搜索树。
2、二叉搜索树
具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
public void insertTree(Node node,int val){
if(node==null){
root = new Node(val);
return;
}
if(val>= node.val){
if(node.right==null){
node.right = new Node(val);
return;
}
insertTree(node.right,val);
}else {
if(node.left==null){
node.left = new Node(val);
return;
}
insertTree(node.left,val);
}
}
上面就是排序树的建立方法,我们可以发现的树会有很多空节点。
平衡二叉树
如何判断是一棵二叉树?
只要左右节点的高度差小于二,那么他是一个平衡二叉树。
首先需要获得树的高度,层序遍历
public int treeHeight(Node node){
if(node==null){
return 0;
}
Queue<Node> queue = new LinkedList<>();
queue.offer(node);
int preQueueSize = queue.size();
int height = 1;
while (!queue.isEmpty()){
if(preQueueSize==0){
preQueueSize=queue.size();
height++;
}
preQueueSize--;
Node queuePoll = queue.poll();
if(queuePoll.left!=null){
queue.offer(queuePoll.left);
}
if(queuePoll.right!=null){
queue.offer(queuePoll.right);
}
}
return height;
}
判断其是二叉树
public boolean isBalance(Node node){
if(node==null){
return true;
}
if(!isBalance(node.left)){
return false;
}
if(!isBalance(node.left)){
return false;
}
return Math.abs(treeHeight(node.left) - treeHeight(node.right)) < 2;
}
构建二叉树
当我们插入新的节点的数据
RR 失衡
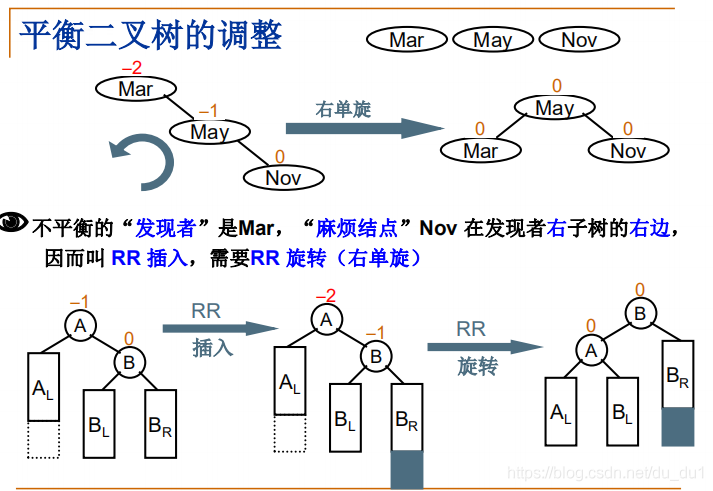
public Node rightRightRotation(Node node){
Node returnNode = node.right;
node.right = returnNode.left;
returnNode.left = node;
return returnNode;
}
RL 失衡
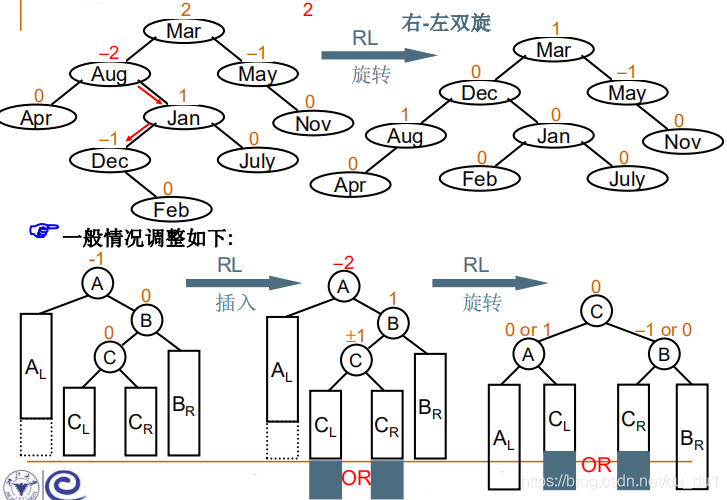
// RL 旋转 先右后左旋转 即右旋变为RR 再左单旋转
public Node rightLeftRotation(Node node){
Node nodeRight = node.right;
Node returnNode = nodeRight.left;
nodeRight.left = returnNode.right;
returnNode.right = nodeRight;
// 左单旋转
node.right = returnNode.left;
returnNode.left = node;
return returnNode;
}
LL 失衡
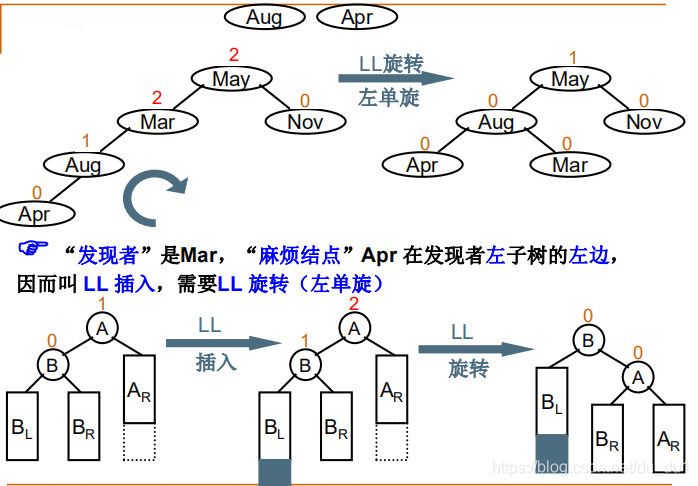
// LL 旋转 右单旋转
public Node leftLeftRotation(Node node){
Node returnNode = node.left;
node.left = returnNode.right;
returnNode.right = node;
return returnNode;
}
LR 失衡
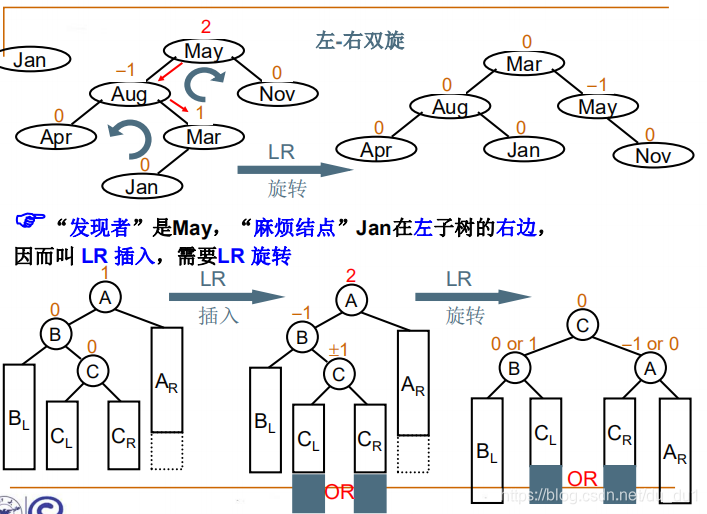
// LR 旋转 先左后右旋转 即先左旋变为LL 再右旋
public Node leftRightRotation(Node node){
// 先左旋转
Node nodeLeft = node.left;
Node returnNode = nodeLeft.right;
nodeLeft.right = returnNode.left;
returnNode.left = nodeLeft;
// 右单旋转
node.left = returnNode.right;
returnNode.right = node;
return returnNode;
}
全部代码
package com.company;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
public class Node {
int val;
Node left;
Node right;
public Node(int val) {
this.val = val;
}
}
class AVLTree{
Node root;
// 中序遍历
public void middleView(Node node){
if(node==null){
return;
}
middleView(node.left);
System.out.println(node.val);
middleView(node.right);
}
// 迭代 中序遍历
public void middleViewStack(Node node){
Stack<Node> stack = new Stack<>();
// 我们需要有个node 辅助来记录之前的值
Node assitNode = node;
while (!stack.empty()||assitNode!=null){
if(assitNode==null){
assitNode = stack.pop();
System.out.println(assitNode.val);
assitNode = assitNode.right;
continue;
}
stack.push(assitNode);
assitNode = assitNode.left;
}
}
public void insertTree(Node node,int val){
if(node==null){
root = new Node(val);
return;
}
if(val>= node.val){
if(node.right==null){
node.right = new Node(val);
return;
}
insertTree(node.right,val);
}else {
if(node.left==null){
node.left = new Node(val);
return;
}
insertTree(node.left,val);
}
}
public Node insertAvlTree(Node node, int val){
if(node==null){
return new Node(val);
}
if(val>=node.val){
node.right = insertAvlTree(node.right,val);
if(Math.abs(treeHeight(node.left)-treeHeight(node.right))>=2){
// 代表不是平衡二叉树
if(val>node.right.val){
return rightRightRotation(node);
}else{
return rightLeftRotation(node);
}
}
}else {
node.left = insertAvlTree(node.left,val);
if(Math.abs(treeHeight(node.left)-treeHeight(node.right))>=2){
// LL 右单旋转
if(val< node.left.val){
return leftLeftRotation(node);
}else {
// LR
return leftRightRotation(node);
}
}
}
return node;
}
public int treeHeight(Node node){
if(node==null){
return 0;
}
Queue<Node> queue = new LinkedList<>();
queue.offer(node);
int preQueueSize = queue.size();
int height = 1;
while (!queue.isEmpty()){
if(preQueueSize==0){
preQueueSize=queue.size();
height++;
}
preQueueSize--;
Node queuePoll = queue.poll();
if(queuePoll.left!=null){
queue.offer(queuePoll.left);
}
if(queuePoll.right!=null){
queue.offer(queuePoll.right);
}
}
return height;
}
// LL 旋转 右单旋转
public Node leftLeftRotation(Node node){
Node returnNode = node.left;
node.left = returnNode.right;
returnNode.right = node;
return returnNode;
}
// LR 旋转 先左后右旋转 即先左旋变为LL 再右旋
public Node leftRightRotation(Node node){
// 先左旋转
Node nodeLeft = node.left;
Node returnNode = nodeLeft.right;
nodeLeft.right = returnNode.left;
returnNode.left = nodeLeft;
// 右单旋转
node.left = returnNode.right;
returnNode.right = node;
return returnNode;
}
// RR 旋转 左单旋转
public Node rightRightRotation(Node node){
Node returnNode = node.right;
node.right = returnNode.left;
returnNode.left = node;
return returnNode;
}
// RL 旋转 先右后左旋转 即右旋变为RR 再左单旋转
public Node rightLeftRotation(Node node){
Node nodeRight = node.right;
Node returnNode = nodeRight.left;
nodeRight.left = returnNode.right;
returnNode.right = nodeRight;
// 左单旋转
node.right = returnNode.left;
returnNode.left = node;
return returnNode;
}
public boolean isBalance(Node node){
if(node==null){
return true;
}
if(!isBalance(node.left)){
return false;
}
if(!isBalance(node.left)){
return false;
}
return Math.abs(treeHeight(node.left) - treeHeight(node.right)) < 2;
}
}
class test{
public static void main(String[] args) {
int[] arrays = {9,4,1,354,5,4,8,1,3,16};
AVLTree avlTree = new AVLTree();
for(int i:arrays){
avlTree.root = avlTree.insertAvlTree(avlTree.root,i);
}
avlTree.middleViewStack(avlTree.root);
System.out.println("root val " + avlTree.root.val);
System.out.println("height " + avlTree.treeHeight(avlTree.root));
System.out.println("is right " + avlTree.isBalance(avlTree.root));
AVLTree avlTreeNoAvl = new AVLTree();
for(int i:arrays){
avlTreeNoAvl.insertTree(avlTreeNoAvl.root,i);
}
avlTreeNoAvl.middleView(avlTree.root);
System.out.println("root val " + avlTreeNoAvl.root.val);
System.out.println("height " + avlTreeNoAvl.treeHeight(avlTreeNoAvl.root));
System.out.println("is right " + avlTreeNoAvl.isBalance(avlTreeNoAvl.root));
}
}
后面
简化旋转
// LL 旋转 左单单旋转
public Node leftLeftRotation(Node node){
Node returnNode = node.left;
node.left = returnNode.right;
returnNode.right = node;
return returnNode;
}
// LR 旋转 先左单 后右单
public Node leftRightRotation(Node node){
// 先左旋转
node.left = rightRightRotation(node.left);
// 后右旋转
return leftLeftRotation(node);
}
// RR 旋转 左单旋转
public Node rightRightRotation(Node node){
Node returnNode = node.right;
node.right = returnNode.left;
returnNode.left = node;
return returnNode;
}
// RL 旋转 先右后左旋转 即右旋变为RR 再左单旋转
public Node rightLeftRotation(Node node){
node.right = leftLeftRotation(node.right);
return rightRightRotation(node);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号