筛法

筛法是重要的数论基础，介绍一下\(Eratosthenes\)和\(Euler\)筛法，还有线性筛求\(\varphi\)函数和\(\mu\)函数。

\(Eratosthenes\)筛法

也就是我们常说的埃氏筛法。
时间复杂度：\(\mathcal{O}\left(n\log\log n\right)\)
空间复杂度：\(\mathcal{O}\left(n\right)\)

原理

这是小学五年级下册的数学书，图中框出的两句话就是两种筛法思想。

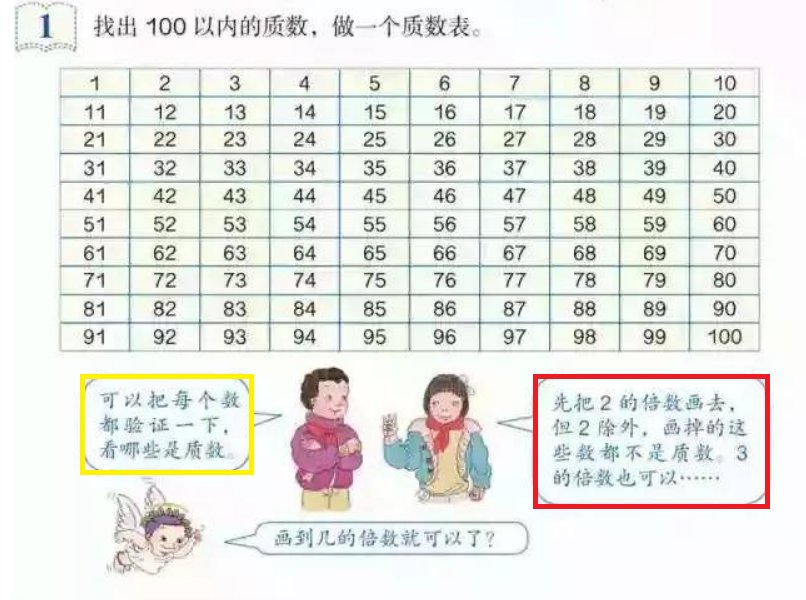
我们来看黄框的思想，概括来说就是对每个数做一次素性检验。众所周知，素性检验最简单的写法是\(\mathcal{O}\left(\sqrt{n}\right)\)的，，所以总共需要\(\sum\limits_{i=1}^{n}\sqrt{i}\)（式子的展开）次计算，可见时间复杂度不优。
红框的思想就是埃筛的思想，对于每一个数标记它的倍数，我们顺序循环，如果一个数被循环到时还没被标记，那么它就是质数，这个思想很聪明，它的时间复杂度是\(\mathcal{O}\left(n\log\log n\right)\)的（OI_wiki上的证明+Mertens'Proof of Mertens'Theorem
）
我不会证，所以放一些参考资料。
在实际实现中，用\(bitset\)的效率比用\(bool\)数组高，详见OI_wiki上的数据测试，效率貌似比\(Euler\)筛要快。

\(Code\):

const int N=1e8+5;
bitset<N>bs;
ll prime[N],tot=0; 
void Eratosthenes(int n){
	bs[0]=bs[1]=true;
	for(ll i=2;i<=n;i++){
		if(!bs[i]){
			prime[++tot]=i;
			if((ll)(i*i)<=n){
				for(ll j=i*i;j<=n;j+=i){
					bs[j]=true;
				}
			}
		}
	}
}

\(Euler\)筛

时间复杂度：\(\mathcal{O}\left(n\right)\)
空间复杂度：\(\mathcal{O}\left(n\right)\)
实际上常数偏大，在\(n\)小时效率不如埃筛。

思想+\(Code\)

首先交换循环顺序，我们考虑筛去\(i\)的所有质数倍，先看代码。

void init(int n) {
    for (int i = 2; i <= n; ++i) {
        if (!vis[i]) {
            pri[cnt++] = i;
        }
        for (int j = 0; j < cnt; ++j) {
            if (1ll * i * pri[j] > n) break;
            vis[i * pri[j]] = 1;
            if (i % pri[j] == 0) {
                break;
            }
        }
    }
}

\(pri\left[i\right]\mid i\)时\(break\)，这是唯一的不同，我们考虑一下。当\(i\)是\(pri\left[i\right]\)的倍数时，\(i\)的任意倍都会被\(pri\left[i\right]\)筛掉，所以这里不用继续筛。

线性筛求\(\varphi\)函数

注意到,在线性筛中,每个合数都被最小素因子筛掉。设\(p_{1}\)是\(n\)的最小素因子,则设\(n'=\frac{n}{p_{1}}\)。
如果\(p_{1}\mid n'\),那么\(n'\)包含了\(n\)所有种类的素因子。
\({\begin{array}{l}\varphi\left(n\right)=n\times\prod\limits_{i=1}^{k}\frac{p_{i}-1}{p_{i}}\\ \ \ \ \ \ \ \ \ \ \ =p_{1}\times n'\prod\limits_{i=1}^{k}\frac{p_{i}-1}{p_{i}}\\ \ \ \ \ \ \ \ \ \ \ =p_{1}\times\varphi\left(n'\right) \end{array}}\)
如果\(p_{1}\nmid n'\),那么\(\left(n',p_{1}\right)=1\)
\(\therefore \varphi\left(n\right)=\varphi\left(n'\right)\times\varphi\left(p_{1}\right)=\left(p_{1}-1\right)\varphi\left(n'\right)\)

实现

int phi[N],p[N];
bool v[N];  
void pre(){
    memset(v, 1, sizeof(v));
    int cnt = 0;
    v[1] = 0;
    phi[1] = 1;
    for (int i = 2; i <= N; i++) {
        if (v[i]) {
            p[++cnt] = i;
            phi[i] = i - 1;
        }
        for (int j = 1; j <= cnt && i * p[j] <= N; j++) {
            v[i * p[j]] = 0;
            if (i % p[j])
            phi[i * p[j]] = phi[i] * phi[p[j]];
            else {
            phi[i * p[j]] = phi[i] * p[j];
                break;
            }
        }
    }
}

线性筛求\(\mu\)函数

同上设
\(\mu\left(n\right)=\left\{\begin{matrix}-1\cdots\left [n\text{为质数}\right]\\ 0\cdots \left[p_{1}\mid n'\right]\\ -\mu\left(n'\right)\cdots\left[otherwise\right]\end{matrix}\right.\)

实现

void pre(){
    mu[1] = 1;
    int tot=1;
    for (int i = 2; i <= 1e7; ++i) {
        if (!v[i]) mu[i] = -1, p[++tot] = i;
        for (int j = 1; j <= tot && i <= 1e7 / p[j]; ++j) {
            v[i * p[j]] = 1;
            if (i % p[j] == 0) {
                mu[i * p[j]] = 0;
                break;
            } else {
            mu[i * p[j]] = -mu[i];
            }
        }
    }
}