可持久化数组

写在前面

我是蒟蒻，不会区间修改，只知道要标记永久化。

可持久化线段树

思想

可持久化数组要求修改之前的版本，所以我们必须保存之前的版本，但是对于每次都再建一颗线段树，空间是极大的，所以我们考虑优化。
我们修改图中的黄色节点，线段树从前一棵变为了后一棵。

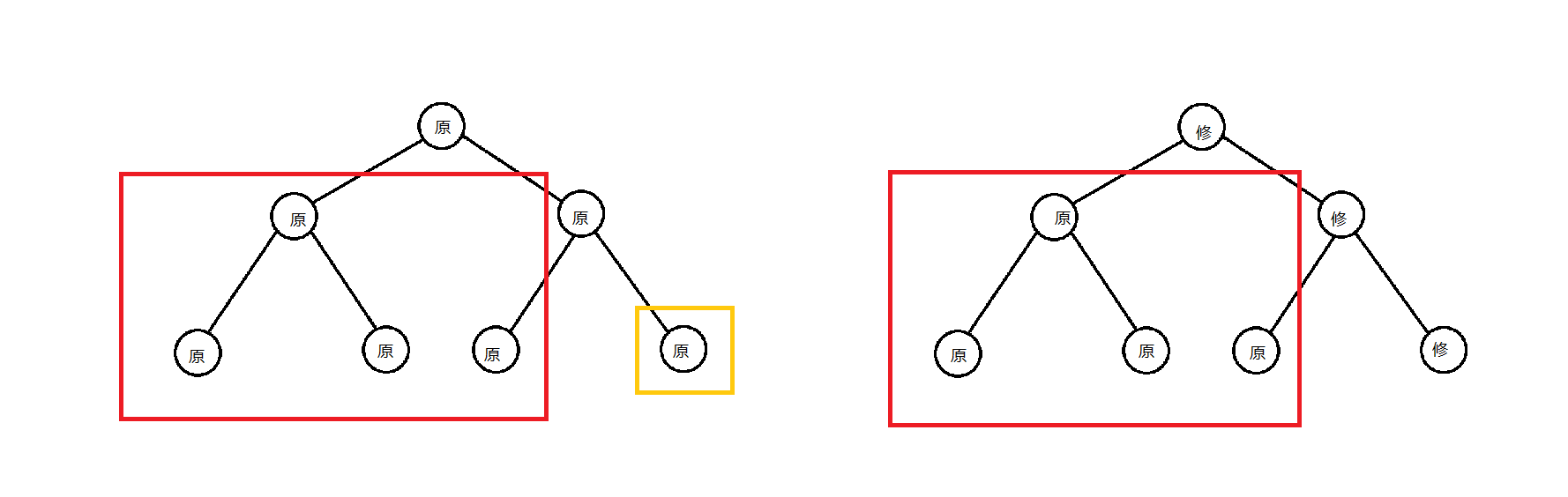
注意到，图中的红色框中的节点是相同的，所以我们考虑重复利用节点。
下图展示了可持久化数组的结构。

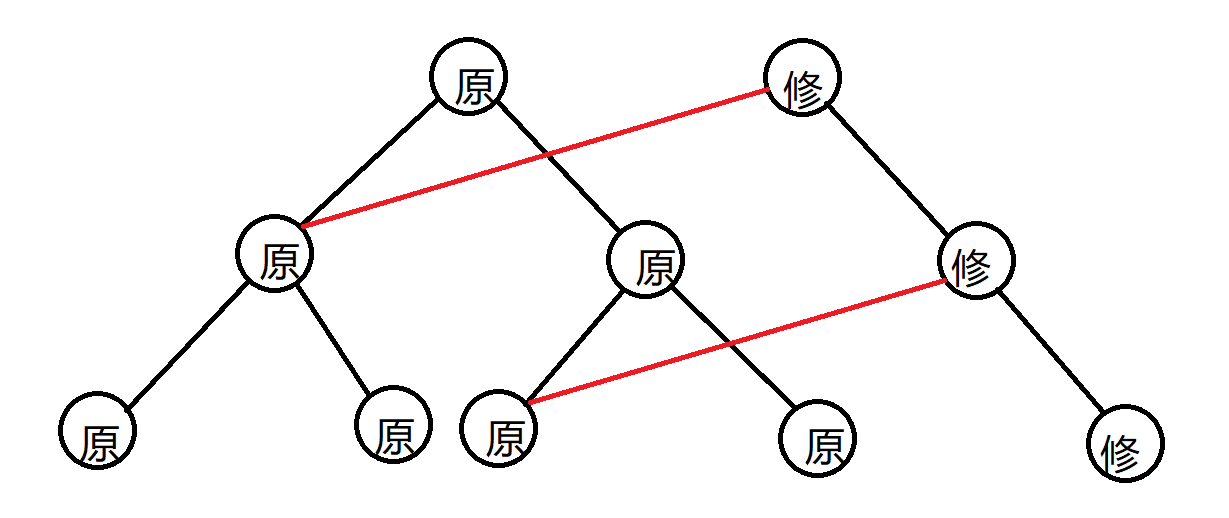
图中的红色连边是重复利用节点的关键，我们注意到三个关键点：
\(1.\)图中不只有一个根节点。
\(2.\)每一个根节点都构成一棵线段树，都对应一个版本。
\(3.\)每一次修改只会增加\(\log_{2}n\)个节点。
所以现在实现思路就很明显了，下面结合代码讲解具体操作。

节点结构

由于每次复制版本时需要新建\(\log_2 n\)个节点，所以左子节点和右子节点不能再用\(i\times 2\)与\(i\times 2+1\)表示，要单独记录。

tips:
可持久化数组的空间复杂度\(O(n+mlog_{n})\)，注意\(n\)实际为\(4n\)，本题中\(m=n,n=10^{6}\)，众所周知\(log_{2}10^{6}\approx 20\)，所以空间实际上要开到\(24n\)，至少位移\(5\)位。

\(Code:\)

struct node{
	int l,r,val;//节点的储存，分别为：左子节点，右子节点，点权值
}tree[N<<5];//要注意细节，空间要开到24倍，所以至少位移5位

建树

建树操作与普通线段树的区别不大。
\(Code:\)

int build(int left,int right){//建树
	int i=++tot;//给新节点编号
	if(left==right){//到叶节点
		tree[i].val=read();//读入边权
		tree[i].l=tree[i].r=INF;//没有左右孩子
		return i;//返回节点编号
	}
	int mid=left+right>>1;//递归建左右子树
	tree[i].l=build(left,mid);//伪指针指向左孩子
	tree[i].r=build(mid+1,right);//伪指针指向右孩子
	return i;//返回节点编号
}

单点修改

我们已经知道，每一个根节点对应一个版本，所以只要在对应的线段树上做单点修改就可以了。注意新建节点。
\(Code:\)

int update(int i,int left,int right,int x,int y){//修改操作
	int point=copy(i);//复制i节点
	if(left==right){//到根节点
		tree[point].val=y;//修改权值
		//tree[point].l=tree[point].r=INF;
	}
	else{//没找到
		int mid=left+right>>1;//递归去找
		if(x<=mid)tree[point].l=update(tree[point].l,left,mid,x,y);
		else tree[point].r=update(tree[point].r,mid+1,right,x,y);
	}
	return point;
}

由于修改没有区别，所以不解释。

完整代码