并查集专题

被老师拖来讲数据结构了

带权并查集

带权并查集，顾名思义，就是在并查集中加上权值，点权和边权实际上是等价的，因为并查集实际上是多棵树组成的，树上的每个节点，都只有一个父节点，因此点权和边权可以互相转化，在这里，我们将权值视为点到父节点的权值，也就是边权。

介绍

并查集的优化中最重要的就是路径压缩，下面来介绍带权并查集的路径压缩。

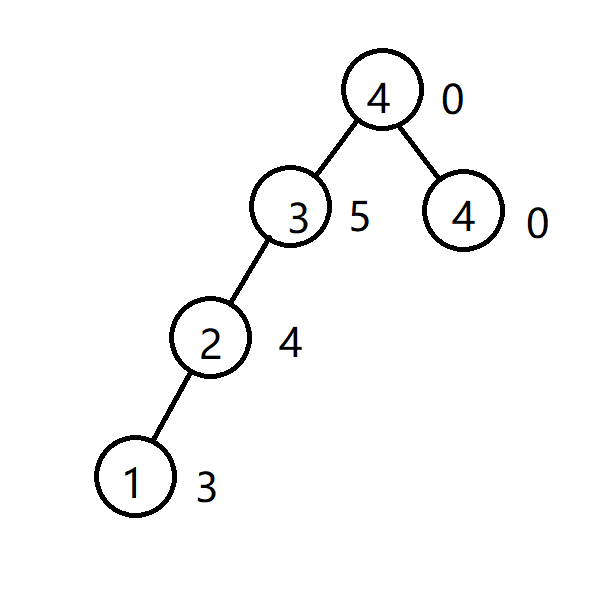
如图，这是一个还未路径压缩的并查集结构，圆圈中是节点的编号，旁边是点权值。
带权并查集的操作，不仅要判断二者是否在一个集合内，而且要能够知道一个点到根节点的权值之和。

路径压缩

我们将\(i\)点的点权记为\(d\left[i\right]\)。
带权并查集中的路径压缩，就是将从询问点到根节点的链上的所有权值和加起来。

tips：
例子中权值是简单的相加，题目中可能有相乘，按位与，按位或，按位异或等，要视题而定。

如上图，\(1\)号节点权值为\(d[1]\),压缩后记为\(d[1]'\),则\(d[1]'=d[1]+d[2]+d[3]\)

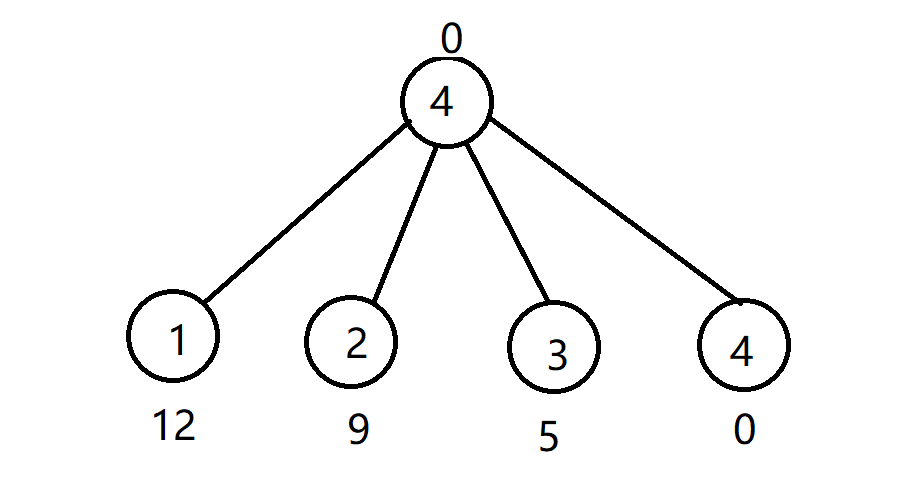
如图，这是查询\(1\)号节点之后压缩的结果。
这显然是很好编码的。
\(Code:\)

int find(int x){
	if(x!=fa[x]){
		int t=fa[x];
		fa[x]=find(fa[x]);
		d[x]+=d[t];
	}
	return fa[x];
}

合并

由于有边权，所以合并操作也并没有那么简单。
我们记增加的边边权为\(s\).要连接\(x,y\)所在的集合。
首先我们要先做\(find(x),find(y)\)两个操作，这个操作有两个作用：
\(1.\)获取\(x\),\(y\)的集合的代表。
\(2.\)将\(x\),\(y\)直接连到代表节点上。
记\(find(x)=f_{x},find(y)=f_{y}\)，那么连边如下图所示。

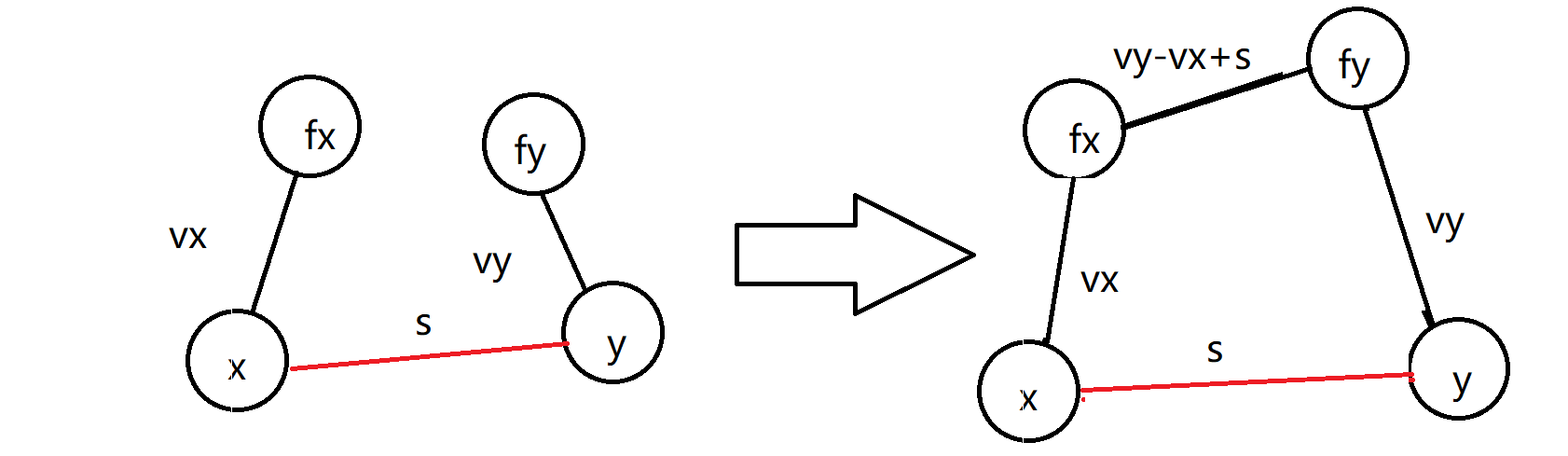
图中红色边是帮助理解的边，按照定义，路径\(len(x\to y\to f_{y})=len(x\to f_{x]}\to f_{y})\)，而事实上是这样的，这也是\(len(f\to f_{y})=v_{y}-v_{x}+s\)的原因。
结合图感性理解一下。
\(Code:\)

void merge(int x,int y,int s){
	int fx=find(x),fy=find(y);
	if(fx!=fy){
		fa[fx]=fy;
		d[fx]=d[y]-d[x]+s;
	}
}

扩展域并查集

扩展域并查集要解决多个逻辑冲突问题的:有两个集合，共有\(m\)个条件，\(n\)个\({a_{i}}\)与\({b_{i}}\)，每个条件形如\((a,b)\)，表示\(a,b\)不能放在同一个集合中。求出是否能解决。

思路

事实上，这个只要讲思想可以了。
对于每一个\(a\)，拆为\(\neg a\)与\(a\)。对于每个条件\((a,b)\)，将\(a\)与\(\neg b\)放入一个集合中，将\(\neg a\)与\(b\)放入另一个集合中，最后判断是否存在\(a\)与\(\neg a\)在一个集合中，如果存在就不能解决，反之则然。在实现中，将\(\neg a\)记为\(a+n\)号节点。

可撤销并查集

可撤销并查集支持三种操作：
\(1.\)合并两个集合。
\(2.\)回退到上一次\(1\)操作前的状态。
\(3.\)查询元素所在集合。
时间复杂度要求：
操作\(1:O(\log n)\)。
操作\(2:O(1)\)。
操作\(3:O(\log n)\)。

实现

由于路径压缩破坏了原先树形结构，撤销十分困难。
所以我们退而求其次，使用按秩合并。
对于每次操作，我们使用栈来记录操作。每一次回退，就弹出栈顶。
\(Code:\)

struct node{
	int a,b;
	node(int x,int y){
		a=x,b=y;
	}
};
stack<node>s;
int find(int x){
	if(x!=fa[x])return find(fa[x]);
	return fa[x];
}
void merge(int u,int v){
	int x=find(u),y=find(v);
	if(x!=y){
		if(siz[x]<siz[y])swap(x,y);
		s.push(node(x,siz[x]));
		s.push(node(y,fa[y]));
		siz[x]+=siz[y];
		fa[y]=x;
	}
}
void undo(){
	node now=s.top();
	s.pop();
	fa[now.a]=now.b;
	now=s.top();
	s.pop();
	siz[now.a]=now.b;
}