前缀和与差分

by CamusJohnson 转载请注明出处 https://www.cnblogs.com/jccodingforfun01/p/12763105.html

前缀和

一维前缀和

现有数组a，构造数组b，使得 b[i] = a[1] + a[2] + ··· + a[i]
方法：

for(int i = 1; i <= n; i++)  
    b[i] = b[i-1] + a[i]；

作用：快速得到a数组一段区间的和 a[j] + a[j+1] + ··· + a[i] = b[i] - b[j-1]

注意 a[0] = 0

二维前缀和（子矩阵）

现有矩阵A，构造矩阵B，使得

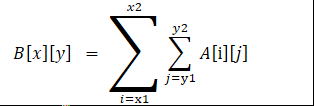
通俗地讲就是B[x][y]等于A[x][y]左上方的子矩阵的和。


方法：

for(int i = 1; i <= x; i++)
    for(int j = 1; j <= y; j++)
        B[i][j] = B[i][j-1] + B[i-1][j] - B[i-1][j-1] + A[i][j]; 

作用：快速求出

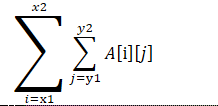
公式为：B[x2][y2] - B[x2][y1-1] - B[x1-1][y2] + B[x1-1][y1-1] (画个图就理解了)

注意 B[i][0] = 0,B[0][j] = 0

差分

一维差分

现有数组a，构造数组b使得 a[i] = b[1] + b[2] + ··· + b[i]，即a是b的前缀和
这里等一下再讲构造方法
作用：在O(1) 的时间内让a数组l到r区间加上常数c
方法

void insert(int l, int r,int c){
    b[l] += c;
    b[r+1] -= c;
}

好！我们回过去讲构造方法，我们先把数组a看全是0的数组，然后把区间(i,i)的0加上a[i]。代码如下

for(int i = 1; i <= n; i++)
    insert(i,i,a[i]);

二维差分

现有矩阵A，构造矩阵B，使得

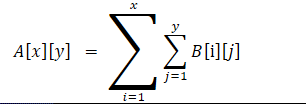
即数组A是数组B的子矩阵和。
这里也同样等一下再讲构造方法，聪明的小伙伴已经知道为什么了。
作用是在O（1） 的时间内让矩阵A 的一个子矩阵加上常数c。这里记子矩阵为A[x1][y1]为最左上角元素，A[x2][y2]为最右下角元素。方法如下

void insert(int x1,int y1,int x2,int y2,int c){
    B[x1][y1] += c;
    B[x2+1][y1] -= c;
    B[x1][y2+1] -= c;
    B[x2+1][y2+1] += c;
}
insert(x1,y1,x2,y2,c);

构造方法自然是先把A矩阵看成全是0的矩阵，然后在每个位置上加上元素本身，方法如下：

for(int i = 1; i <= n; i++)
    for(int j = 1; j <= m; j++) insert(i,j,i,j,A[i][j]);

例题

前缀和与差分是处理数据很好的方法，因为大大降低了时间复杂度
下面看个例题，这是codeforces 636div3的D题，题不算难，但也不算模板题了。

D. Constant Palindrome Sum
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output

You are given an array a consisting of n integers (it is guaranteed that n is even, i.e. divisible by 2). All ai does not exceed some integer k.
Your task is to replace the minimum number of elements (replacement is the following operation: choose some index i from 1 to n and replace ai with some integer in >range [1;k]) to satisfy the following conditions:
after all replacements, all ai are positive integers not greater than k;
for all i from 1 to n2 the following equation is true: ai+an−i+1=x, where x should be the same for all n2 pairs of elements.
You have to answer t independent test cases.

Input
The first line of the input contains one integer t (1≤t≤104) — the number of test cases. Then t test cases follow.
The first line of the test case contains two integers n and k (2≤n≤2⋅105,1≤k≤2⋅105) — the length of a and the maximum possible value of some ai correspondingly. It is >guratanteed that n is even (i.e. divisible by 2). The second line of the test case contains n integers a1,a2,…,an (1≤ai≤k), where ai is the i-th element of a.
It is guaranteed that the sum of n (as well as the sum of k) over all test cases does not exceed 2⋅105 (∑n≤2⋅105, ∑k≤2⋅105).

Output
For each test case, print the answer — the minimum number of elements you have to replace in a to satisfy the conditions from the problem statement.

这道题的意思是给定长度为n(n是偶数)的数组a和一个值k，可以把数组中任意一个值改成不超过k的值，问最少经过几次这样的操作使得所有a[i] + a[n+1-i]的值相等 思路是这样定义一个b数组，b[j] 的含义是把a数组改成a[i] + a[n+1-i] = j 时的最少操作。显然，j最大值为2k。对于一对a[i] 和 a[n+1-i]，区间[1,min(a[i],a[n+1-i]))∪（max（a[i],a[n+1-i]）+k,2k]的b[j] 增加 2， b[a[i] + a[n+1-i]] 增加 0， 区间[min(a[i],a[n+1-i],a[i]+a[n+1-i]))∪(a[i]+a[n+1-i],max(a[i],a[n+1-i]+k)]的b[j]增加1，遍历i = 1到n/2 完成b数组，然后取最小值。但是遍历i的同时，每一个i需要遍历j，时间复杂度达到10^10量级，一定会超掉。这时我们用差分来维护数组b，就可以优化。附上AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
typedef unsigned long long int Ull;
template <typename T>
inline T  read()
{
    char c=getchar();
    T x=0,f=1;
    while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
    while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return x*f;
}
template <typename T>
inline void write(T x) 
{
    if(x < 0) x = (~x) + 1, putchar('-');
    if(x / 10) write(x / 10);
    putchar(x % 10 | 48);
}
const int INF = 0x3f3f3f3f;
const int N = 1e5+5;
int b[4*N];
int arr[2*N];
void insert(int l, int r,int c){
    b[l] += c;
    b[r+1] -= c;
}
int main(){
    //ios_base::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int T = read<int>();
    while(T--){
        int n = read<int>(), k = read<int>();
        for(int i = 0; i <= k*2; i++) b[i] = 0;
        for(int i = 1; i <= n; i++) arr[i] = read<int>();
        for(int i = 1; i <= n/2; i++){
            int Max = max(arr[i],arr[n-i+1]) + k;
            int Min = min(arr[i],arr[n-i+1]) + 1;
            int s = arr[i] + arr[n-i+1];
            insert(0,Min-1,2);
            insert(Min,s-1,1);
            insert(s+1,Max,1);
            insert(Max+1,2*k,2);
        }
        int ans = INF;
        for(int i = 1; i <= 2*k ; i++){
            b[i] += b[i-1];
            ans = min(ans,b[i]);
        }
        printf("%d\n",ans);
    }
}