建模比赛总结
建模比赛总结
总结一下两次建模比赛用到的算法和模型
建模国赛-省一
使用到的算法/模型:主成分分析,灰色预测,0-1规划
主成分分析
由于问题需要我们确定五十家最重要的供货商,是个很典型的评价问题,评价就需要指标来衡量优劣,但是原文件中没有给出具体的特征,所以需要进行特征提取,但是提取出来的特征很多,可以利用主成分分析法对特征进行降维处理。(用SPSS和python分析)
主成分分析介绍
在减少需要分析的指标同时,尽量减少原指标包含信息的损失,从而达到对收集数据进行全面分析的目的。
降维的优点
-
去除噪声
-
使得数据集更容易使用
主成分分析的主要思想就是将 n 维特征映射到 k 维上,这 k 维也被称为主成分。PCA的工作就是从原始空间中寻找一组相互正交的坐标轴,并挑选出包含绝大部分方差(变化幅度大)的维度特征,忽略剩余维度。
具体步骤:
-
对变量进行标准化
-
计算相关系数矩阵
-
求出相关系数矩阵的特征值并排序
-
计算贡献率(选取贡献率大于80%的主成分)
-
计算每个样本的综合得分(以每个成分的贡献率为权重)
-
将样本根据综合得分排序
结果检验
将数据降维过后的样本和未降维的,以特征值衡量的样本对比,观察综合得分和特征的关系,发现基本符合综合得分越高,相应由特征值表示出来的重要性符合
缺点
-
主成分解释其含义往往具有一定的模糊性
-
PCA 的标准是选取原数据在新坐标轴上方差最大的主成分,但是方差小的特征不一定不重要,有可能会损失信息
-
有损压缩,会损失信息
使用spss进行分析时先用因子分析获得初始因子载荷矩阵,再由载荷矩阵得出相关系数矩阵
python代码
# 数据处理
import pandas as pd
import numpy as np
# 绘图
import seaborn as sns
import matplotlib.pyplot as plt
df = pd.read_csv(r"D:\桌面\aa.csv", encoding='gbk', index_col=0).reset_index(drop=True)
print(df)
# Bartlett's球状检验
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
chi_square_value, p_value = calculate_bartlett_sphericity(df)
print(chi_square_value, p_value)
# KMO检验
# 检查变量间的相关性和偏相关性,取值在0-1之间;KOM统计量越接近1,变量间的相关性越强,偏相关性越弱,因子分析的效果越好。
# 通常取值从0.6开始进行因子分析
from factor_analyzer.factor_analyzer import calculate_kmo
kmo_all, kmo_model = calculate_kmo(df)
print(kmo_all)
# #标准化
# #所需库
# from sklearn import preprocessing
# #进行标准化
# df = preprocessing.scale(df)
# print(df)
# #求解系数相关矩阵
# covX = np.around(np.corrcoef(df.T),decimals=3)
# print(covX)
# #求解特征值和特征向量
# featValue, featVec= np.linalg.eig(covX.T) #求解系数相关矩阵的特征值和特征向量
# print(featValue, featVec)
#不标准化
#均值
def meanX(dataX):
return np.mean(dataX,axis=0)#axis=0表示依照列来求均值。假设输入list,则axis=1
average = meanX(df)
print(average)
#查看列数和行数
m, n = np.shape(df)
print(m,n)
#均值矩阵
data_adjust = []
avgs = np.tile(average, (m, 1))
print(avgs)
#去中心化
data_adjust = df - avgs
print(data_adjust)
#协方差阵
covX = np.cov(data_adjust.T) #计算协方差矩阵
print(covX)
#计算协方差阵的特征值和特征向量
featValue, featVec= np.linalg.eig(covX) #求解协方差矩阵的特征值和特征向量
print(featValue, featVec)
####下面没有区分#######
#对特征值进行排序并输出 降序
featValue = sorted(featValue)[::-1]
print(featValue)
#绘制散点图和折线图
# 同样的数据绘制散点图和折线图
plt.scatter(range(1, df.shape[1] + 1), featValue)
plt.plot(range(1, df.shape[1] + 1), featValue)
# 显示图的标题和xy轴的名字
# 最好使用英文,中文可能乱码
plt.title("Scree Plot")
plt.xlabel("Factors")
plt.ylabel("Eigenvalue")
plt.grid() # 显示网格
plt.show() # 显示图形
#求特征值的贡献度
gx = featValue/np.sum(featValue)
print(gx)
#求特征值的累计贡献度
lg = np.cumsum(gx)
print(lg)
#选出主成分
k=[i for i in range(len(lg)) if lg[i]<0.85]
k = list(k)
print(k)
#选出主成分对应的特征向量矩阵
selectVec = np.matrix(featVec.T[k]).T
selectVe=selectVec*(-1)
print(selectVec)
#主成分得分
finalData = np.dot(data_adjust,selectVec)
print(finalData)
#绘制热力图
plt.figure(figsize = (14,14))
ax = sns.heatmap(selectVec, annot=True, cmap="BuPu")
# 设置y轴字体大小
ax.yaxis.set_tick_params(labelsize=15)
plt.title("Factor Analysis", fontsize="xx-large")
# 设置y轴标签
plt.ylabel("Sepal Width", fontsize="xx-large")
# 显示图片
plt.show()
# 保存图片
# plt.savefig("factorAnalysis", dpi=500)
灰色预测
题目要求我们根据前五年的数据来选择未来24周(不妨设该24周就是从第一周开始)的最佳供应商,首先需要预测出所有供货商未来24周的供货量,由于供货商的供货量和时间相关,随时间有很大变化,不能简单用一个均值或别的单一数字代替供货量,并简单乘以24。更好的办法是在前五年数据的基础上,构造时间序列。具体如下:
-
将每一家供货商每年第一周,第二周....的数据分别取出
-
将每年的第一周的数据组成时间序列,利用这个序列预测下一年的第一周数据,以此类推
背景及计算
灰色预测本身只适用于时间序列短,统计数据少,信息不完全的系统,在这种情况下,具有非常显著的功效,正适合本文中的数据量较少的情况。
灰色预测通过鉴别系统之中各数据的关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势。使用等时距的数据(在本问题中,就是前五年中每隔一年的数据)预测未来某一时刻的特征量。
步骤:
-
使用累加把无规律数列变为递增数列\(X^{(1)}\),要求初始序列

-
利用\(X^{(1)}\) 生成\(Z^{(1)}\) :MEAN序列

-
首先进行级比检验,判断是否适合建模分析
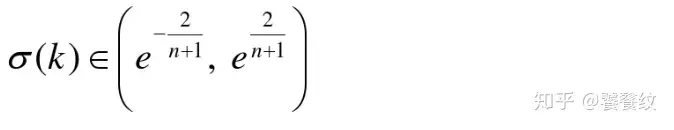
-
利用最小二乘法计算参数a,b

-
得到a,b之后,代入白化方程中得出时间响应序列,并得到\(X^{(1)}(k+1)\) 的值,并计算预测值

结果检验
残差检验,相对误差检验,级比偏差值检验
拓展-大量数据的预测
线性回归,决策树(回归,分类),
支持向量机(分类):用来解决二分类问题的机器学习算法,它通过在样本空间中找到一个划分超平面,将不同类别的样本分开,同时使得两个点集到此平面的最小距离最大,两个点集的边缘点到此平面的距离最大,
-
距离划分线最近的几个样本点叫做支持向量
-
分类
-
清晰线性可分的:硬间隔支持向量机
-
训练数据近似线性可分:软间隔支持向量机
-
线性不可分时:可以使用核技巧以及软间隔最大化,学习非线性支持向量机
-
美赛-H
找出音乐影响的有向图,并衡量网络中的音乐影响
-
入度
-
聚类系数:反应删除该节点后对整个图连通性的影响
查询论文得到系数\(\alpha\),综合两个参数得到节点重要性,使用networkx库绘制有向图
在衡量相似度时,使用主成分分析降维,找到音乐风格显著变化的时间,并将变化后的音乐综合得分和变化之前的音乐家进行对比,找到革命的引领者。在分析音乐流派是否相似时,使用余弦相似度算法来计算相似程度


 浙公网安备 33010602011771号
浙公网安备 33010602011771号