线性模型——机器学习(西瓜书)读书笔记
第3章 线性模型
3.2 线性回归
将训练集中的特征和标记拟合到某个线性函数上,然后运用此线性函数寻找测试集中特征对应的标记(预测)。
对属性(特征)的描述:对离散属性,若属性值间存在“序”关系,可通过连续化将其转化为连续值。如属性“身高”的取值高、中、低可转化为{1.0, 0.5, 0.0};若属性值间不存在序关系,假定有 k 个属性值,通常转化为 k 维向量,如“瓜类”的取值“西瓜”、“南瓜”、“黄瓜”可转化为(0, 0, 1)、(0, 1, 0)、(1, 0, 0)。
注:1.关键在于找到所对应的线性函数(求解w和b),常用的方法有:最小二乘法和极大似然法。(两种不同的数学方法,均有效)
2.在多元(多个特征)的情况下,在求解线性函数的参数时往往涉及求逆矩阵问题,此时需考虑是否存在唯一解(满秩与否),若存在多解,那么需要引入正则化项(惩罚项)来找到最优解。
3.线性回归也可以通过引入非线性映射来实现非线性函数拟合,被称为广义线性模型。广义线性模型的参数同样可以通过最小二乘法或极大似然法进行估计。
4.线性模型(二分法)对比于SVM时,以最小二乘法为例,从几何上看,线性模型求参数时考虑的是每个样本点到线性函数的纵向距离和最短,而SVM考虑距离超平面的最近的那几个样本点(支持向量)之间的间隔最小。
3.3 对数几率回归(二分类)
基于线性模型的二分类任务一般是通过把回归模型产生的预测值(实数)进行转化,转化后的0/1则代表两类标记。而常用的转化方式为单位阶跃函数,实际上是将线性回归模型的预测(实数)进行阶跃处理,其结果作为预测结果。但问题是单位阶跃函数不连续,所以以sigmoid为替代的对数几率回归应运而生。
用对数几率函数可以对分类的可能性进行建模,等式一边是“对数几率”,另一边是线性函数对训练集中样本的拟合。
可以理解为,1.用线性函数对训练集中的样本进行拟合;
2.拟合后对预测集上的样本进行预测;
3.预测的结果进行对数几率的映射;
4.用预测结果的对数几率去逼近真实标记的对数几率。
几何上理解:1.最终目标是找到一个划分,使得在测试集中划分的最为准确;
2.首先要考虑训练集,要让训练集中的大多数样本都正确划分;
3.其次用一些方法(单位阶跃、对数几率),使得划分不过分突兀(单位阶跃太突兀,对数几率平滑);
4.运用数学方法(极大似然法)找到最优的划分。
算法:
理论:
(目标:确定w和b)
(建模:)
新的广义线性模型为: 可变化为:
设y为后验估计,代表在样本x下,样本为正例的概率。
同理,可得:
(样本为正例的概率)
(样本为反例的概率)
(估计:)
似然项令为: (给定一个样本,估计对的概率)
似然函数则为: (所有样本都估计对了的概率再取对数)
(凸优化:)
运用梯度上升法、牛顿法、拟牛顿法等等均可求得最优解
3.4 softmax回归
简介
该模型是logistic回归模型在多分类问题上的推广,在多分类问题中,类标签  可以取两个以上的值。 Softmax回归模型对于诸如MNIST手写数字分类等问题是很有用的,该问题的目的是辨识10个不同的单个数字。Softmax回归是有监督的,不过它也可以与深度学习/无监督学习方法相结合。(注: MNIST 是一个手写数字识别库,由NYU 的Yann LeCun 等人维护。http://yann.lecun.com/exdb/mnist/ )
可以取两个以上的值。 Softmax回归模型对于诸如MNIST手写数字分类等问题是很有用的,该问题的目的是辨识10个不同的单个数字。Softmax回归是有监督的,不过它也可以与深度学习/无监督学习方法相结合。(注: MNIST 是一个手写数字识别库,由NYU 的Yann LeCun 等人维护。http://yann.lecun.com/exdb/mnist/ )
在 softmax回归中,我们解决的是多分类问题(相对于 logistic 回归解决的二分类问题),类标  可以取
可以取  个不同的值(而不是 2 个)。因此,对于训练集
个不同的值(而不是 2 个)。因此,对于训练集  ,我们有
,我们有 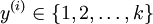 。(注意此处的类别下标从 1 开始,而不是 0)。例如,在 MNIST 数字识别任务中,我们有
。(注意此处的类别下标从 1 开始,而不是 0)。例如,在 MNIST 数字识别任务中,我们有 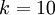 个不同的类别。
个不同的类别。
对于给定的测试输入  ,我们想用假设函数针对每一个类别j估算出概率值
,我们想用假设函数针对每一个类别j估算出概率值 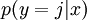 。也就是说,我们想估计
。也就是说,我们想估计  的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个
的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个  维的向量(向量元素的和为1)来表示这
维的向量(向量元素的和为1)来表示这  个估计的概率值。 具体地说,我们的假设函数
个估计的概率值。 具体地说,我们的假设函数 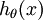 形式如下:
形式如下:
其中 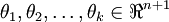 是模型的参数。请注意
是模型的参数。请注意 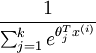 这一项对概率分布进行归一化,使得所有概率之和为 1 。
这一项对概率分布进行归一化,使得所有概率之和为 1 。
为了方便起见,我们同样使用符号  来表示全部的模型参数。在实现Softmax回归时,将
来表示全部的模型参数。在实现Softmax回归时,将  用一个
用一个 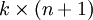 的矩阵来表示会很方便,该矩阵是将
的矩阵来表示会很方便,该矩阵是将 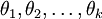 按行罗列起来得到的,如下所示:
按行罗列起来得到的,如下所示: 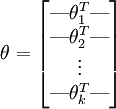
代价函数:
在下面的公式中,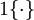 是示性函数,其取值规则为:
是示性函数,其取值规则为:
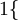 值为真的表达式
值为真的表达式 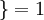 ,
, 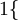 值为假的表达式
值为假的表达式 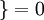 。
。
举例来说,表达式 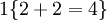 的值为1 ,
的值为1 ,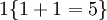 的值为 0。
的值为 0。
代价函数为:
值得注意的是,上述公式是logistic回归代价函数的推广。logistic回归代价函数可以改为:
可以看到,Softmax代价函数与logistic 代价函数在形式上非常类似,只是在Softmax损失函数中对类标记的  个可能值进行了累加。注意在Softmax回归中将
个可能值进行了累加。注意在Softmax回归中将  分类为类别
分类为类别  的概率为:
的概率为:
![p(y^{(i)} = j | x^{(i)} ; \theta) = \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)}} }]() .
.
对于  的最小化问题,目前还没有闭式解法。因此,我们使用迭代的优化算法(例如梯度下降法,或 L-BFGS)。经过求导,我们得到梯度公式如下:
的最小化问题,目前还没有闭式解法。因此,我们使用迭代的优化算法(例如梯度下降法,或 L-BFGS)。经过求导,我们得到梯度公式如下:
让我们来回顾一下符号 "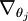 " 的含义。
" 的含义。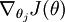 本身是一个向量,它的第
本身是一个向量,它的第  个元素
个元素 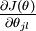 是
是  对
对 的第
的第  个分量的偏导数。
个分量的偏导数。
有了上面的偏导数公式以后,我们就可以将它代入到梯度下降法等算法中,来最小化  。
。
例如,在梯度下降法的标准实现中,每一次迭代需要进行如下更新: 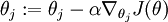 (
(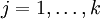 )。
)。
当实现 softmax 回归算法时, 我们通常会使用上述代价函数的一个改进版本。具体来说,就是和权重衰减(weight decay)一起使用。我们接下来介绍使用它的动机和细节。
Softmax回归模型参数化的特点
Softmax 回归有一个不寻常的特点:它有一个“冗余”的参数集。为了便于阐述这一特点,假设我们从参数向量  中减去了向量
中减去了向量  ,这时,每一个
,这时,每一个 都变成了
都变成了 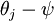 (
(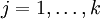 )。此时假设函数变成了以下的式子:
)。此时假设函数变成了以下的式子:
换句话说,从  中减去
中减去  完全不影响假设函数的预测结果!这表明前面的 softmax 回归模型中存在冗余的参数。更正式一点来说, Softmax 模型被过度参数化了。对于任意一个用于拟合数据的假设函数,可以求出多组参数值,这些参数得到的是完全相同的假设函数
完全不影响假设函数的预测结果!这表明前面的 softmax 回归模型中存在冗余的参数。更正式一点来说, Softmax 模型被过度参数化了。对于任意一个用于拟合数据的假设函数,可以求出多组参数值,这些参数得到的是完全相同的假设函数 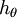 。
。
进一步而言,如果参数 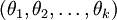 是代价函数
是代价函数  的极小值点,那么
的极小值点,那么 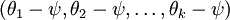 同样也是它的极小值点,其中
同样也是它的极小值点,其中  可以为任意向量。因此使
可以为任意向量。因此使  最小化的解不是唯一的。(有趣的是,由于
最小化的解不是唯一的。(有趣的是,由于  仍然是一个凸函数,因此梯度下降时不会遇到局部最优解的问题。但是 Hessian 矩阵是奇异的/不可逆的,这会直接导致采用牛顿法优化就遇到数值计算的问题)
仍然是一个凸函数,因此梯度下降时不会遇到局部最优解的问题。但是 Hessian 矩阵是奇异的/不可逆的,这会直接导致采用牛顿法优化就遇到数值计算的问题)
注意,当 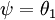 时,我们总是可以将
时,我们总是可以将  替换为
替换为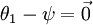 (即替换为全零向量),并且这种变换不会影响假设函数。因此我们可以去掉参数向量
(即替换为全零向量),并且这种变换不会影响假设函数。因此我们可以去掉参数向量  (或者其他
(或者其他  中的任意一个)而不影响假设函数的表达能力。实际上,与其优化全部的
中的任意一个)而不影响假设函数的表达能力。实际上,与其优化全部的 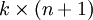 个参数
个参数 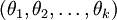 (其中
(其中 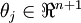 ),我们可以令
),我们可以令 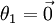 ,只优化剩余的
,只优化剩余的 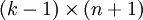 个参数,这样算法依然能够正常工作。
个参数,这样算法依然能够正常工作。
在实际应用中,为了使算法实现更简单清楚,往往保留所有参数 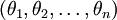 ,而不任意地将某一参数设置为 0。但此时我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
,而不任意地将某一参数设置为 0。但此时我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
权重衰减(正则化)
我们通过添加一个权重衰减项(正则化项) 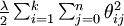 来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
有了这个权重衰减项以后 (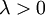 ),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为
),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为 是凸函数,梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。
是凸函数,梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。
为了使用优化算法,我们需要求得这个新函数  的导数,如下:
的导数,如下:
通过最小化  ,我们就能实现一个可用的 softmax 回归模型。
,我们就能实现一个可用的 softmax 回归模型。
Softmax回归与Logistic 回归的关系
当类别数 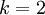 时,softmax 回归退化为 logistic 回归。这表明 softmax 回归是 logistic 回归的一般形式。具体地说,当
时,softmax 回归退化为 logistic 回归。这表明 softmax 回归是 logistic 回归的一般形式。具体地说,当 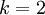 时,softmax 回归的假设函数为:
时,softmax 回归的假设函数为:
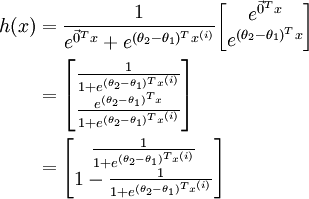
利用softmax回归参数冗余的特点,我们令 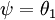 ,并且从两个参数向量中都减去向量
,并且从两个参数向量中都减去向量  ,得到:
,得到:
因此,用 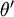 来表示
来表示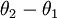 ,我们就会发现 softmax 回归器预测其中一个类别的概率为
,我们就会发现 softmax 回归器预测其中一个类别的概率为 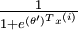 ,另一个类别概率的为
,另一个类别概率的为 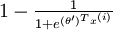 ,这与 logistic回归是一致的。
,这与 logistic回归是一致的。
Softmax 回归 vs. k 个二元分类器
如果你在开发一个音乐分类的应用,需要对k种类型的音乐进行识别,那么是选择使用 softmax 分类器呢,还是使用 logistic 回归算法建立 k 个独立的二元分类器呢?
这一选择取决于你的类别之间是否互斥,例如,如果你有四个类别的音乐,分别为:古典音乐、乡村音乐、摇滚乐和爵士乐,那么你可以假设每个训练样本只会被打上一个标签(即:一首歌只能属于这四种音乐类型的其中一种),此时你应该使用类别数 k = 4 的softmax回归。(如果在你的数据集中,有的歌曲不属于以上四类的其中任何一类,那么你可以添加一个“其他类”,并将类别数 k 设为5。)
如果你的四个类别如下:人声音乐、舞曲、影视原声、流行歌曲,那么这些类别之间并不是互斥的。例如:一首歌曲可以来源于影视原声,同时也包含人声 。这种情况下,使用4个二分类的 logistic 回归分类器更为合适。这样,对于每个新的音乐作品 ,我们的算法可以分别判断它是否属于各个类别。
现在我们来看一个计算视觉领域的例子,你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是:室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢? (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片,你又会选择 softmax 回归还是多个 logistic 回归分类器呢?
在第一个例子中,三个类别是互斥的,因此更适于选择softmax回归分类器 。而在第二个例子中,建立三个独立的 logistic回归分类器更加合适。
小结:特征互斥,选择softmax;特征不互斥,选择多个logistic。(选择softmax可以分得更开,选择多个logistic可以把样本的特征分清楚)
3.6类别不平衡时的情况
若训练集是真实总体的无偏采样,直接用logistic回归方法可以得到比较好的分类。但现实情况中,无偏采样的假设往往不成立,即存在样本类别不平衡情况。
若训练样本中的类别不平衡,用一般方法训练出的学习器可能会泛化性能低下。(类别不平衡指分类任务中不同类别的训练样本数量差别很大,例如1个正例99个反例)
对于类别不平衡情况,技术上通常有三类方法解决:
1.直接对训练集中的多的类样例进行“欠采样”,即去掉一些样例,使得正例反例的数目接近。(缺点:可能丢弃重要信息,影响分类器的泛化能力。EasyEnsemble算法利用集成学习机制,将反例划分为若干个集合,供不同的学习器使用,这样每个学习器都进行了欠采样,但在全局看来又不会丢失信息)
2.对训练集中少的类样例进行“过采样”,即增加一些样例,使得正例反例的数目相近。(缺点:若只对少数的样例进行重抽样,容易导致过拟合。SMOTE算法是通过对少数样例进行插值,从而产生样例)
3.直接对训练集学习,但是在分类器预测时,将“再缩放”后的分类器放回(被称为阈值移动)。
通过修改分类器决策规则来修正不平衡问题:将分类器决策规则改为,当 时,预测为正例,否则为反例。因为之后的分类器仍是通过判断,当
时,预测为正例,所以我们将分类器进行再缩放操作。
再缩放:
完成再缩放之后的步骤与logistic回归一致。
再缩放也是代价敏感学习(cost-sensitive learning)的基础。(代价敏感学习研究非均等代价下的学习)

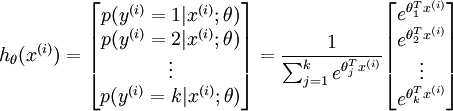
![\begin{align}
J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }}\right]
\end{align}](http://ufldl.stanford.edu/wiki/images/math/7/6/3/7634eb3b08dc003aa4591a95824d4fbd.png)
![\begin{align}
J(\theta) &= -\frac{1}{m} \left[ \sum_{i=1}^m (1-y^{(i)}) \log (1-h_\theta(x^{(i)})) + y^{(i)} \log h_\theta(x^{(i)}) \right] \\
&= - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=0}^{1} 1\left\{y^{(i)} = j\right\} \log p(y^{(i)} = j | x^{(i)} ; \theta) \right]
\end{align}](http://ufldl.stanford.edu/wiki/images/math/5/4/9/5491271f19161f8ea6a6b2a82c83fc3a.png)
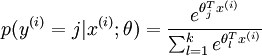 .
.![\begin{align}
\nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} \left( 1\{ y^{(i)} = j\} - p(y^{(i)} = j | x^{(i)}; \theta) \right) \right] }
\end{align}](http://ufldl.stanford.edu/wiki/images/math/5/9/e/59ef406cef112eb75e54808b560587c9.png)
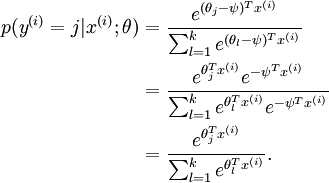
![\begin{align}
J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }} \right]
+ \frac{\lambda}{2} \sum_{i=1}^k \sum_{j=0}^n \theta_{ij}^2
\end{align}](http://ufldl.stanford.edu/wiki/images/math/4/7/1/471592d82c7f51526bb3876c6b0f868d.png)
![\begin{align}
\nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} ( 1\{ y^{(i)} = j\} - p(y^{(i)} = j | x^{(i)}; \theta) ) \right] } + \lambda \theta_j
\end{align}](http://ufldl.stanford.edu/wiki/images/math/3/a/f/3afb4b9181a3063ddc639099bc919197.png)
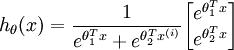

 浙公网安备 33010602011771号
浙公网安备 33010602011771号