部分背包-贪心
例子:
背包容量为W=20,有n=3个价值为v={18,15,10},重量为w={25,24,15}的物品。可以部分选择物品加入到背包中,使得背包中的总价值最大,求每件物品的选择配比解向量x。
分析:
- 显然只有将背包填满才能获得最大价值。
- 根据每件物品的单位价值,按照从小到大加入到背包中,就能获得最大价值。
递推式:
- 首先按照单位价值的大小从大到小进行排序,存放在uv中。
- 如果
![]() 将物品i整个加入到背包中。
将物品i整个加入到背包中。
- 如果
![]() 将物品i的部分Wa加入到背包中。
将物品i的部分Wa加入到背包中。
Java实现代码:
public final class exp_5 {
private exp_5(){
}
public static double[] getX(int W,int[] w,int[] v){
//存放单位价值的数组
double[] uv = new double[w.length];
for(int i=0;i<w.length;i++){
uv[i] = (double)v[i]/(double)w[i];
}
//存放结果的X,存放单位价值数组排序后各个下标的pos
double[] X = new double[uv.length];
int[] pos = MathUtil.sort(uv, false);
//解X
for(int i=0;i<uv.length;i++){
if(w[pos[i]] <= W){
X[pos[i]] = 1;
W -= w[pos[i]];
}else{
X[pos[i]] = (double)W/(double)w[pos[i]];
W = 0;
}
}
return X;
}
}

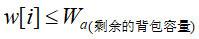 将物品i整个加入到背包中。
将物品i整个加入到背包中。
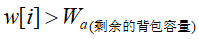 将物品i的部分Wa加入到背包中。
将物品i的部分Wa加入到背包中。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号