0-1背包

什么是0-1背包？

有n个重量分别为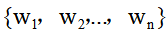的物品，它们的价值分别为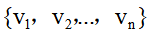，给定一个容量为W的背包。设向量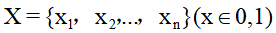表示某个物品是否被选入背包中，在满足约束条件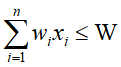的情况下，找出能使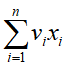取得最大值的解向量X。由于向量X中的每个向量的取值只有0，1，所以该问题被称为0-1背包。

 

分解子问题：

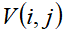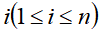设表示将前个物品装入容量为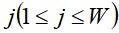的背包获得的最大价值。

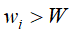1. 如果，则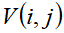=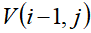。就是放不下的话前i个物品放在容量为j的背包中所获得的最大价值等于将前i-1个物品放在容量为j的背包中所获得的最大价值。
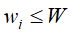2. 如果，则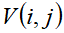=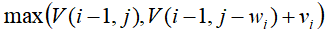。就是如果能放下，看看优先考虑放下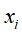所获得的最大价值和不放下所获得的最大价值那个大，取最大值。

    

   动态转移方程：

   

    

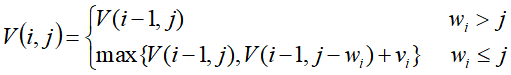
   如何根据V解出向量X？

3. 如果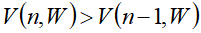说明第n个物品被放入了背包，剩余的前n-1个物品被放入了容量为W-w_n的背包中。
4. 如果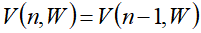说明第n个物品没有被放入背包，剩余的前n-1个物品被放入了容量为W的背包中。

   

    

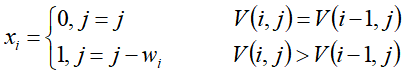
   Java实现代码：

   /**

        * 获取二维表V

        * @param w

        * @param v

        * @param W

        * @return

        */

       public static int[][] Bag01_getV(int[] w,int[] v,int W){

           int[][] V = new int[w.length+1][W+1];

           for(int i=1;i<w.length+1;i++){

               for(int j=1;j<W+1;j++){

                   if(w[i-1]>j){

                       V[i][j] = V[i-1][j];

                   }else{

                       V[i][j] = MathUtil.max(V[i-1][j], V[i-1][j-w[i-1]]+v[i-1]);

                   }

               }

           }

           return V;

       }

       /**

        * 获取解向量X

        * @param V

        * @param w

        * @return

        */

       public static int[] Bag01_getX(int[][] V,int[] w){

           int[] X = new int[V.length-1];

           int j=V[0].length-1;

           for(int i=V.length-1;i>0;i--){

               if(V[i][j] == V[i-1][j]){

                   X[i-1] = 0;

               }else{

                   X[i-1] = 1;

                   j = j-w[i-1];

               }

           }

           return X;

       }