最长公共子序列(LCS)

例子：

有两个字符序列X={A,B,C,B,D,A,B}, Y={B,D,C,A,B,A}, 则Z1={B,D,A,B}, Z2={B,C,B,A}为X与Y的最长公共子序列，如图：

 

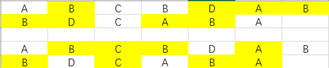
子序列的定义：

给定一个序列X={x₁,x₂,x₃,...,x_m}, 另一个序列Z={z₁,z₂,z₃,...,z_n}, 如果存在一个递增的下标序列{i₁,i₂,i₃,...,i_k,...,i_n}使得x(i_k)=z(k), 那么就称Z为X的子序列。

 

公共子序列的定义：

给定两个序列X,Y如果存在一个序列Z，满足Z是X的子序列，Z是Y的子序列，那么就称Z是X,Y的公共子序列。

 

最长公共子序列(LCS)的定义：

给定两个序列X,Y如果存在一个它们的公共子序列Z，对于任意一个XY的公共子序列的长度，都没有Z的长，则称Z是XY的最长公共子序列。显然最长公共子序列不唯一。

 

如何求出最长公共子序列？

如果我们将X的每一个子序列与Y的每一个子序列的最长公共子序列的长度记录在一个二维数组（表）C中，（C的示例如下图）我们就可以凭借这个二维数组中的值来推算出X与Y的最长公共子序列。那么下面这个最长公共子序列的问题就变成了，如何来求这个二位数组C。

(为了计算的方便，多插入了一行一列全为0的数，写代码时要注意)

 

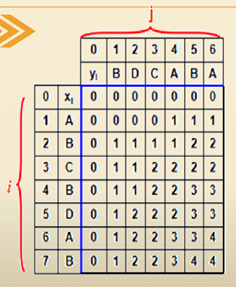
最长公共子序列的性质：

给定两个序列X={x₁,x₂,x₃,...,x_m}, Y={y₁,y₂,y₃,...,y_n}。Z={z₁,z₂,z₃,...,z_k}是XY的一个最长公共子序列。

1. 如果x_m=y_n，那么x_m=y_n=z_k，则X_m-1与Y_n-1的最长公共子序列为Z_k-1。
2. 如果x_m!=y_n，且z_k!=x_m，则X_m-1与Y的最长公共子序列为Z_k-1。
3. 如果x_m!=y_n，且z_k!=y_n，则X与Y_n-1的最长公共子序列为Z_k-1。

    

   递推公式：

   根据最长公共子序列的性质可以得到C的一个递推公式

   

    

   如何根据C来找到最长公共子序列？

   

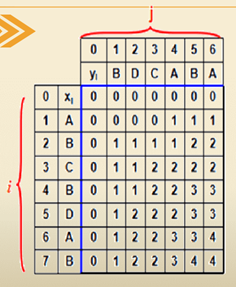
   如图，我们以i=7,j=6为起点开始遍历。

4. 如果x_m=y_n那么就得到了Z中的最后一个元素，并且剩余的其他元素，均包含于Z_k-1。
5. 如果x_m!=y_n，并且C[m-1][n]>=C[m][n-1]，那么Z与Xm-1，Y的最长公共子序列相等。
6. 如果x_m!=y_n，并且C[m-1][n]<C[m][n-1]，那么Z与X，Yn-1的最长公共子序列相等。

    

   Java实现代码：

   /**

        * 获取X的每一个子序列与Y的每一个子序列的最长公共子序列的长度

        * @param X

        * @param Y

        */

       public static int[][] LCS_getLength(char[] X,char[] Y){

           int[][] C = new int[X.length+1][Y.length+1];

           for(int i=0;i<X.length+1;i++){

               for(int j=0;j<Y.length+1;j++){

                   if(i==0 || j==0){

                       C[i][j] = 0;

                   }else if(i>0 && j>0){

                       if(X[i-1]==Y[j-1]){

                           C[i][j] = C[i-1][j-1]+1;

                       }else{

                           C[i][j] = (C[i][j-1]>=C[i-1][j])?C[i][j-1]:C[i-1][j];

                       }

                   }

               }

           }

           return C;

       }

       /**

        * 遍历C表得出其中一个最长公共子序列

        * @param C

        * @param X

        * @param Y

        * @return

        */

       public static char[] LCS_searchSequence(int[][] C,char[] X,char[] Y){

           char[] Z = new char[C[C.length-1][C[0].length-1]];

           int i=C.length-1;

           int j=C[0].length-1;

           for(int k=Z.length-1;k>=0;){

               if(X[i-1]==Y[j-1]){

                   Z[k] = X[i-1];

                   i--;

                   j--;

                   k--;

               }else{

                   if(C[i-1][j]>=C[i][j-1]){

                       i--;

                   }else{

                       j--;

                   }

               }

           }

           return Z;

       }