编译原理笔记(二)之词法分析
1. 词法分析中的若干问题
程序设计语言的基本元素———单词的集合
词法分析器的双重含义:(定义规则和执行规则)
- 规定单词形式的规则,也被称为构词规则或词法规则(立法)
- 根据构词规则识别输入序列,也被称为词法分析(执法)
1.1 基本概念
- 模式:将产生和识别单词的规则
- 记号:按照某个模式(规则)识别出的元素
- 单词:被识别出的元素自身的值
1.2 记号的属性
- 记号至少包含两个部分:记号类别和记号的其他信息
- 记号的类别唯一标识一类记号
- 一般情况下,记号的类别可以用整型编码或枚举类型表示。
1.3 词法分析器的作用与工作方式
- 主要工作:
- 滤掉源程序中无用成分
- 处理与具体平台有关的输入
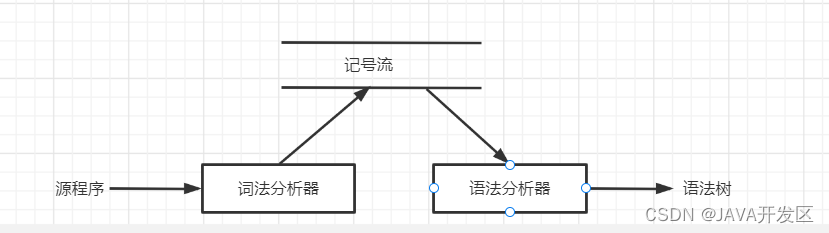
- 识别记号,并交给语法分析器
- 调用符号表管理器或出错处理器,进行相关处理
- 工作方式:
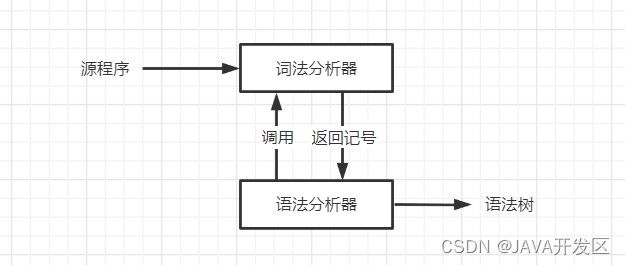
1、 词法分析器作为语法分析器的子程序
![在这里插入图片描述]()
2、 词法分析器单独进行一遍扫描

3、 与语法分析器并行工作的模式
1.4 输入缓冲区
设立输入缓冲区来加快读入源程序字符序列的速度
方式:但缓冲器和双缓冲区
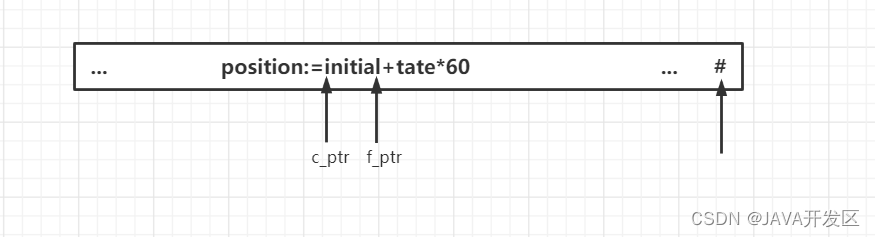
c_ptr:指向当前被识别记号的第一个字符
f_ptr:指向当前被识别记号的向前扫描的字符,向前扫描,直到某个模式匹配成功。
#:表示整个输入程序的结束
2. 模式的形式化描述
从词法分析的角度看,程序设计语言是由记号组成的集合,每个记号又是由若干个字母按照一定规则组成的字符串。
2.1 字符串与语言
- 定义:语言L是有限字母表∑上有限长度字符串的集合。
- 1、字母表是有限的,即字母表中的元素是有限多个。
- 2、字符串的长度是有限的,即字符串中字符的个数是有限多个。
2.2 正规式与正规集
定义:令∑是一个有限字母表,则∑上的正规式及其表示的集合递归定义如下:
(1)ε (伊普西龙)是正规式,它表示集合L(ε)={ε}。
(2)若a是∑上的字符,则a是正规式,它表示集合L(a)={a}。
(3)若正规式r和s分别表示集合L(r)和L(s),则
1、r|s是正规式,表示集合L(r) U L(s); (或)
2、rs是正规式,表示集合L(r)L(s); (连接)
3、r*是正规式,表示集合(L(r))*; (闭包)
4、(r)是正规式,表示集合仍然是L(r);
可用正规式描述的语言称为正规语言或正规集。
2.3 记号的说明
用正规式说明记号的公式为:记号=正规式,可以读作“(左边)记号定义为(右边)正规式”,或者“记号是正规式”
3. 记号的识别——有限自动机
3.1 不确定的有限自动机(NFA)
-
定义:NFA是一个五元组 , M= (S , ∑ , move , s0 , F),其中:
(1)S是有限个状态(state)的集合 (全集)
(2)∑是有限个输入字符(包括ε)的集合(字母表)
(3)move是一个状态转移函数,move(si,ch)=sj 表示当前状态si下遇到输入字符ch,则转移到状态sj
(4)s0是唯一的初态(也称开始状态)
(5)F是终态集(也称接受状态集),它是S的子集,包含了所有的终态(F不一定只有一个) -
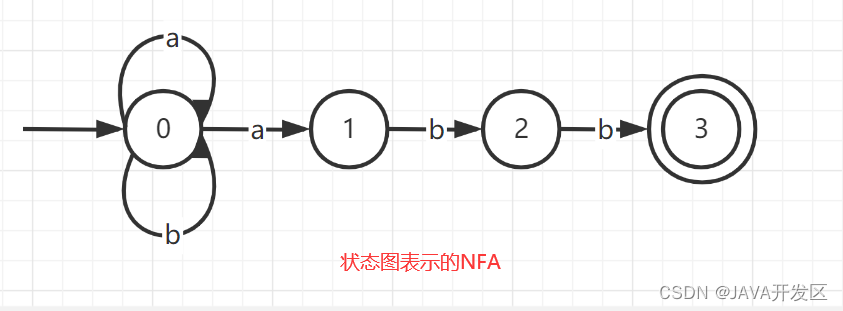
栗子:识别由正规式 (a|b)*abb说明的记号的NFA定义如下:
S ={0,1,2,3},∑={a,b},s0=0,F={3},
move = { move(0,a), move(0,a)=1, move(0,b)=0,move(1,b)=2, move(2,b)=3}
![在这里插入图片描述]()
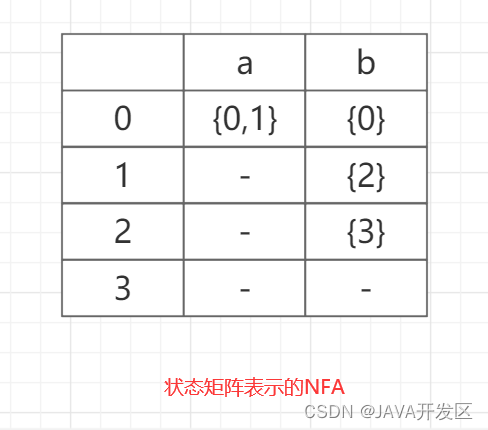
- NFA的特点:不确定性
3.2 确定的有限自动机(DFA)
-
定义:DFA是NFA的一个特列,其中:
(1)没有状态具有ε状态转义,即状态转换图中没有标记ε的边。
(2)对每一个状态s和每一个字符a,最多有一个下一状态。 -
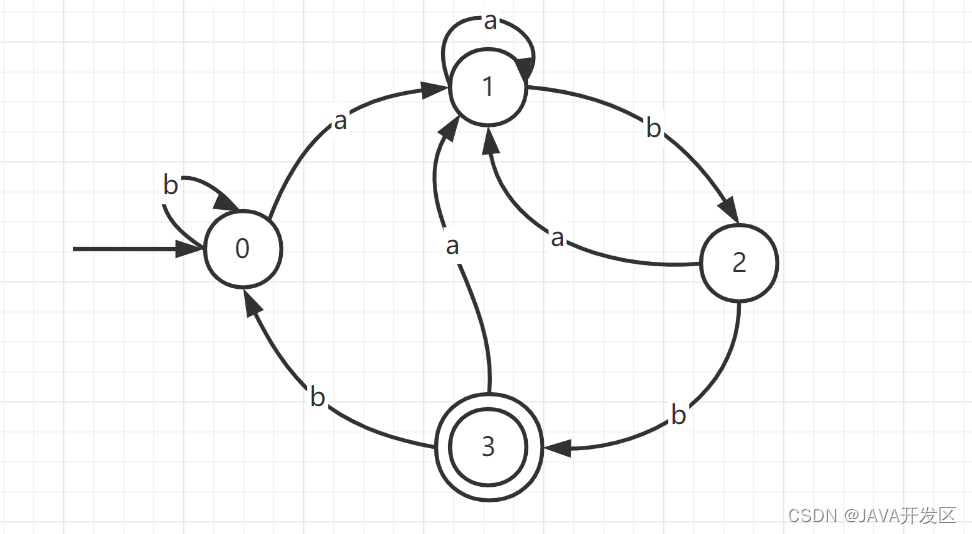
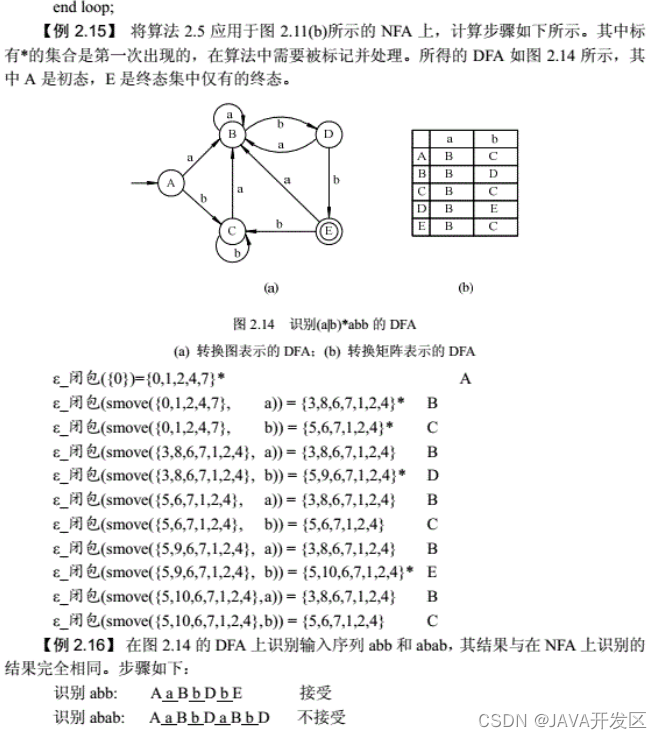
栗子:识别由正规式(a|b)*abb说明的记号的DFA,如图所示
转换图表示的DFA
![在这里插入图片描述]()
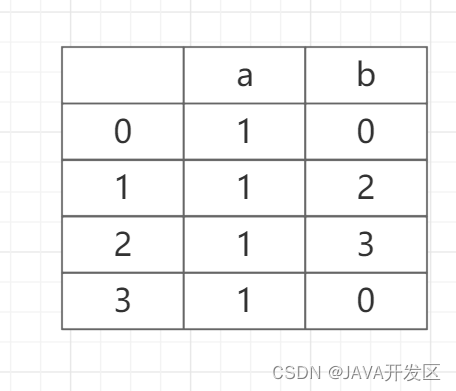
转换矩阵表示的DFA
![在这里插入图片描述]()
-
DFA的特点:确定性
3.3 有限自动机的等价
NFA和DFA统称为有限自动机(FA)。所谓有限,是指自动机的状态数是有限的。
- 定义: 若有限自动机M和M’识别同一个正规集,则称M和M’是等价的,记为M=M‘。
4. 从正规式到词法分析器
构造词法分析器的一般步骤:
- 用正规式对模式进行描述
- 为每个正规式构造一个NFA,它识别正规式所表示的正规集。
- 将构造出来的NFA转换成等价的DFA,这一过程也被称为确定化。
- 优化DFA,使其状态数最少,这一过程称为最小化。
- 根据优化后的DFA构造词法分析器。
4.1 从正规式到NFA
Thompson算法
规则(s0为初态,f为终态):
(1)对于ε,构造NFA。该NFA接受{ε}
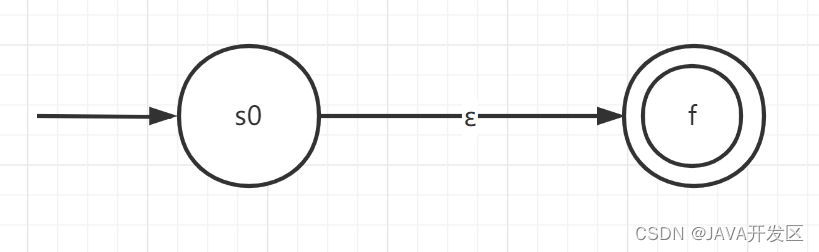
(2)对于∑上的每一个字符a,构造NFA。接受{a}。
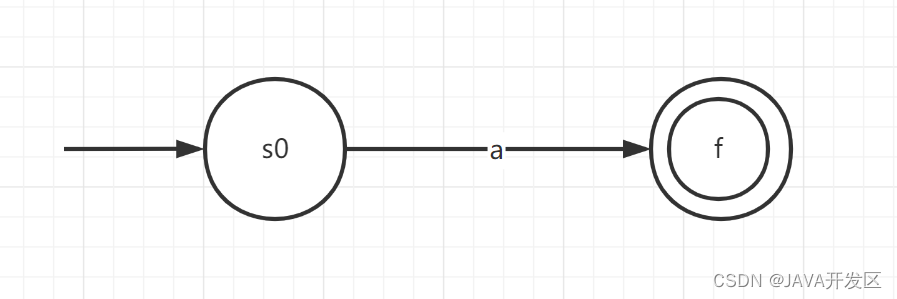
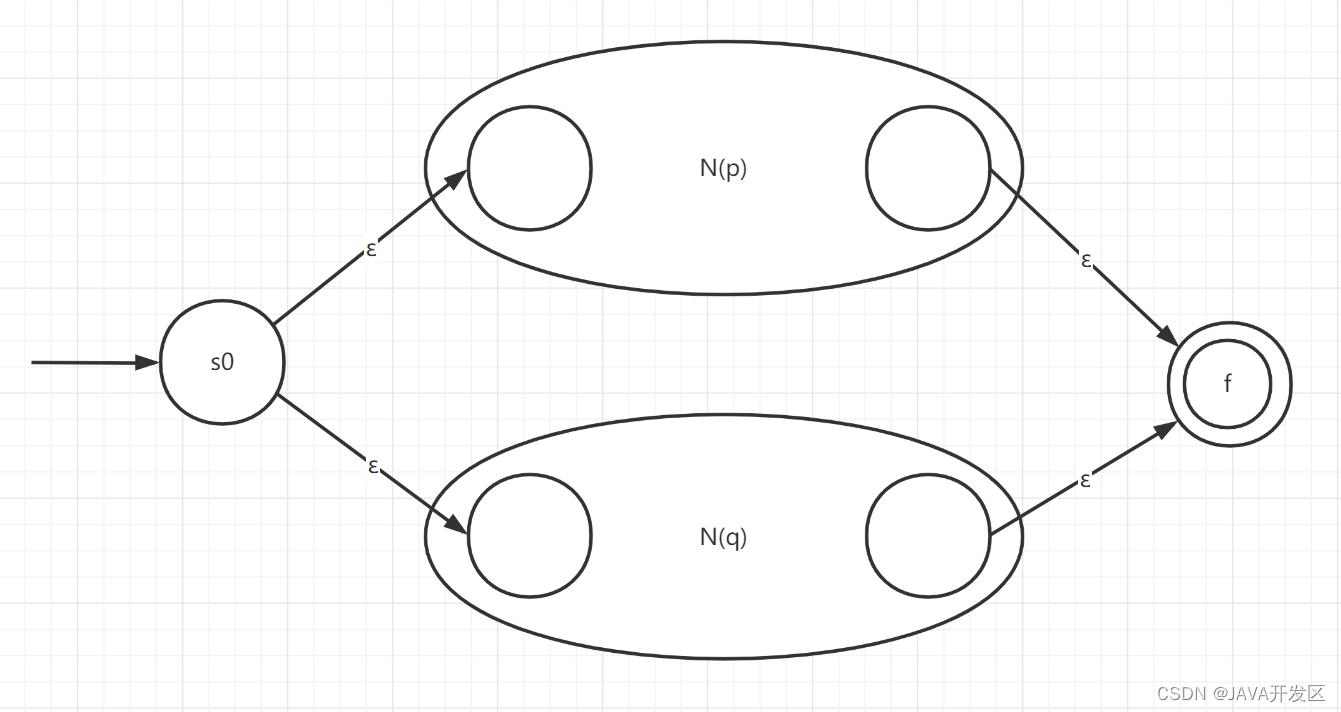
(3) 若N§和N(q)是正规是p和q的NFA,则
1、对于p|q,构造NFA。接受N(p)UN(q)
2、对于正规式pq,构造NFA。接受N(p)N(q)
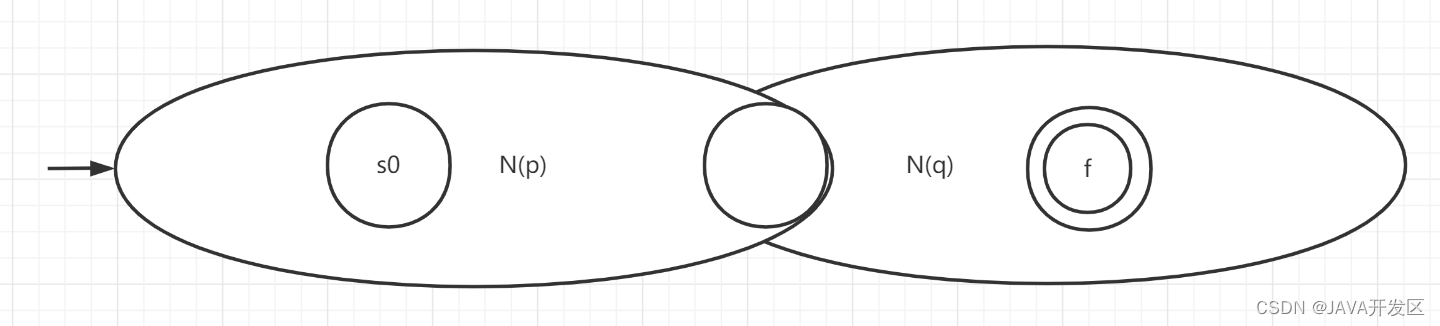
3、对于正规式p*,构造NFA。接受L(p*)

4、对于正规式(p),使用p本身的NFA,不再构造新的NFA
- 栗子:
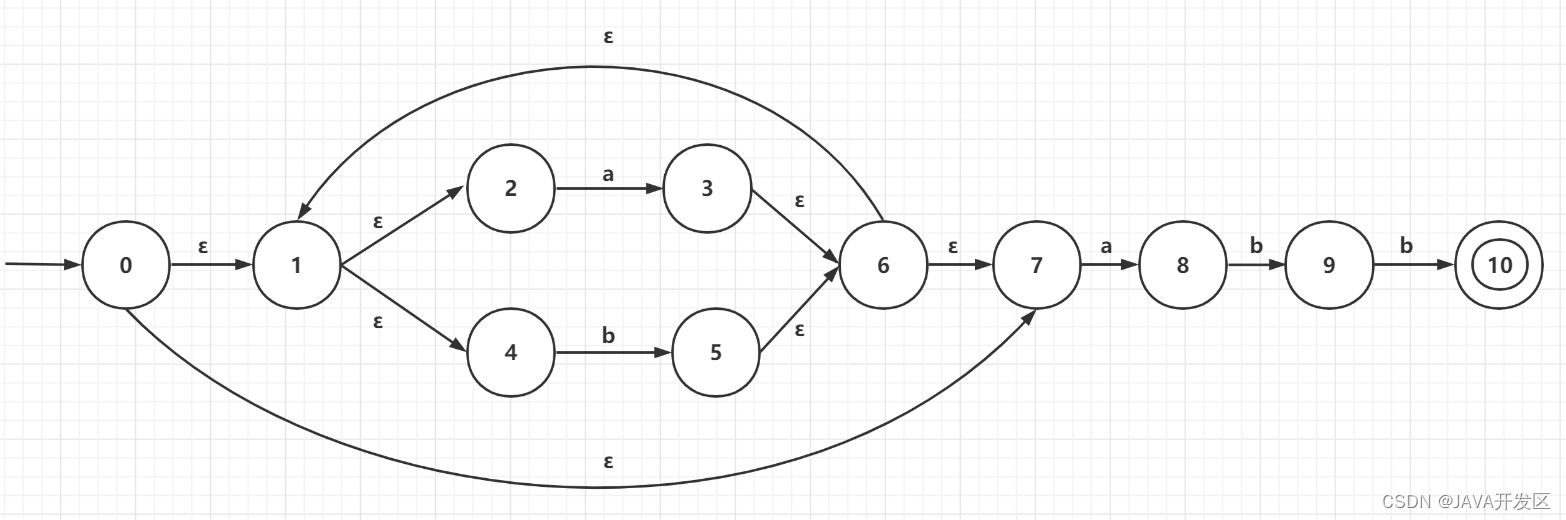
用Thompson算法构造正规式r=(a|b)*abb的N(r)
![在这里插入图片描述]()
4.2 从NFA到DFA
- NFA识别记号的“并行”方法
- 采用并行的方法,可以消除识别时的不确定性,以避免回溯。
- 将不确定的下一状态确定化
![在这里插入图片描述]()
![在这里插入图片描述]()
- “子集法”构造DFA
![在这里插入图片描述]()
![在这里插入图片描述]()
4.3 最小化DFA
将一个DFA等价交换为另一个状态数最少的DFA的过程称为最小化DFA
定义:对于任何两个状态t和s,若从一状态出发接受输入字符串ω,而从另一状态出发不接受ω,或者从t出发和从s出发到达不同的接受状态,则称为ω对状态t和s是可区分的。

4.4 由DFA构造词法分析器
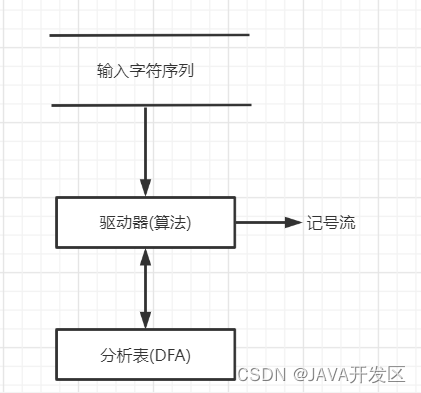
- 表驱动型词法分析器
![在这里插入图片描述]()
驱动器:模拟DFA的算法
分析表:转换矩阵 - 直接编码型词法分析器
直接将DFA转换成程序,即直接用程序代码模拟DFA的行为。
![在这里插入图片描述]()
![在这里插入图片描述]()








 浙公网安备 33010602011771号
浙公网安备 33010602011771号