编译原理笔记(三)之语法分析
1. 语法分析的若干问题
-
分析树和语法树
-
分析语法结构的基本方法:自上而下分析方法和自下而上分析方法
-
语法分析的双重含义:(定义规则和执行规则)
- 规定句子形成的规则,也被称为语法规则,程序设计语言的大部分语法规则可以用==上下文无关文法(CFG)==来描述;(立法)
- 根据语法规则标识记号流中的语言结构,也被称为语法分析。(执法)
1.1 语法分析器的作用
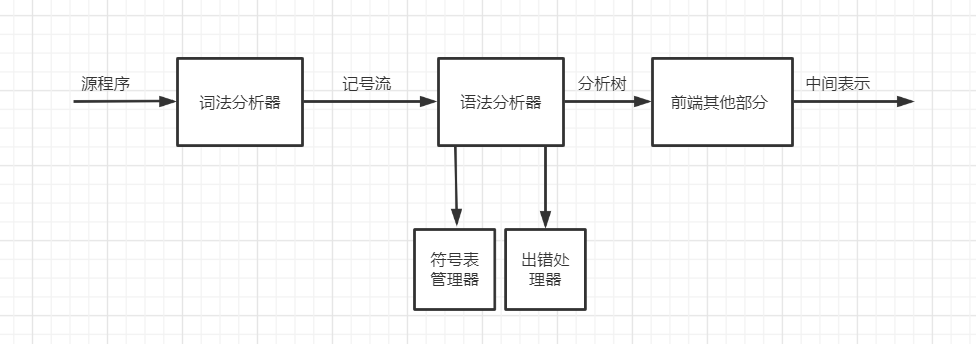
- 根据词法分析器提供的记号流,为语法正确的输入**构造分析树**(或语法树)
- 检查输入中的语法(可能包括词法)错误,并**调用出错处理器**进行适当处理
1.2 语法错误的处理原则
1.2.1 源程序中可能出现的错误
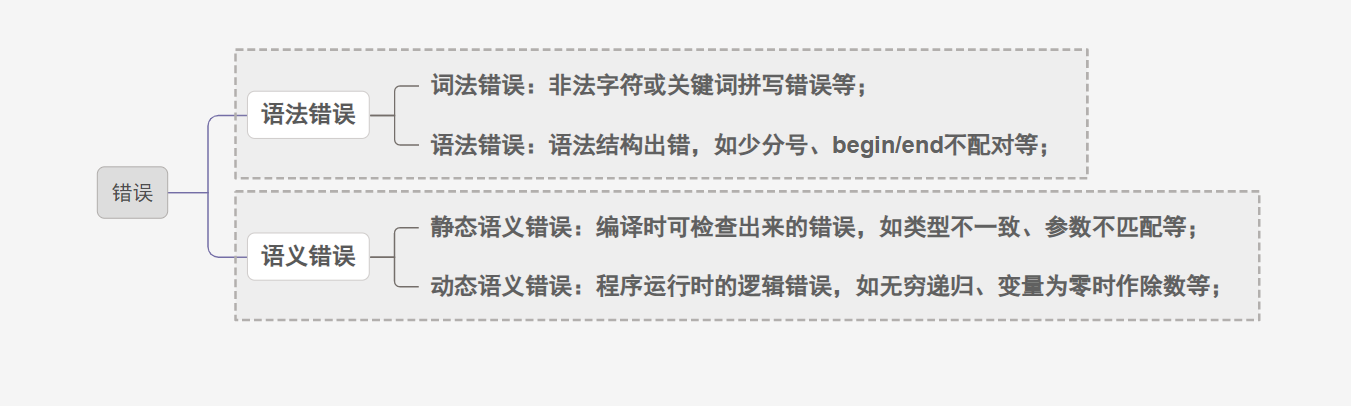
1.2.2 语法错误处理的目标
- 清楚而准确地报告错误的出现,地点正确,不漏报、不错报也不多报。
- 迅速地从每个错误中恢复过来,以便分析继续进行。
- 对语法正确源程序的分析速度不应降低太多。
1.2.3 语法错误的基本恢复策略
- 紧急方式恢复
发现错误时,分析器每次抛弃一个输入记号,一直向前搜索,直到输入记号属于某个指定的合法文法记号(称为同步记号)集合为止。 - 短语级恢复
采用串替换的方式对剩余输入进行局部纠正。
典型的局部纠正是用分号代替逗号,删除多余分号,或者插入遗漏的分号等; - 出错产生式
用出错产生式捕捉错误。这是语法分析器生成器YACC采用的方式,它基本上可以被认为是一种预置型的短语级恢复方式。 - 全局纠正
对有语法错误的输入序列x,根据文法G构造相近序列y的语法树,使得x变换成y所需的修改、插入、删除次数最少。代价太大。
2. 上下文无关文法
2.1 上下文无关文法的定义与表示
定义:上下文无关文法(CFG)是一个四元组G=(N,T,P,S),其中
(1)N是非终结符的有限集合
(2)T是终结符的有限集合,且N∩T=∅
(3)P是产生式的有限集合,每个产生式形如:A->α。其中A∈N,被称为产生式的左部;α∈(N∪T)*,被称为产生式的右部。若α=ε,则称A->ε为空产生式(也可以记为A->)
(4)S是非终结符,被称为文法的开始符号
- 由产生式集表示CFG
由于每个产生式中具有A∈N且α∈(N∪T)*,所以,对于一个没有错误的CFG,可以这样区分N和T集合:
仅N是可以出现在产生式左边的符号的集合
T是词法分析器返回的记号的集合(某些约定的特殊终结符除外),根据N∩T=∅可以推断出T是所有不出现在产生式左边的符号的集合
如果再约定S是第一个产生式的左部,则文法可以由其产生式集P代替,即不写四元组,而仅给出P。CFG的产生式表示也称为巴克斯范式(BNF)。
注意:规范的BNF中,“->”用“::=”表示。 - 产生式的一般读法
“->”读作“定义为”或者“可导出” - 终结符与非终结符书写上的区分
一般情况- 非终结符:大写英文字母A、B、C表示
- 终结符:小写字母a、b、c表示
- 文法符号序列:小写希腊字符α、β、δ表示,即大小写混合的英文字母串
- 产生式的缩写形式
把左部非终结符相同的产生式合并成一个产生式,所有产生式右部由或符号(|)连接,每一个右部现在被称为该产生式的一个候选项,各候选项具有平等的权利。
例如:
<!--文法G3.2-->
E->E+E
|E*E
|(E)
|-E
|id
2.2 CFG产生语言的基本方法——推导
-
可以通过推导的方法产生CFG所描述的语言。非正式地讲,推导就是从文法的开始符号S开始,反复使用产生式,将产生式的左部的非终结符替换成右部的文法符号序列(展开产生式,用标记=>表示),直到得到一个终结符序列(句子).
-
栗子:
-(id+id)可以由文法G3.2产生
E=>-E=>-(E)=>-(E+E)=>-(id+E)=>-(id+id) -
定义:将产生式A->γ的右部代替文法符号序列αAβ中的A得到αγβ的过程,称为αAβ直接推导出αγβ,记作:αAβ=>αγβ
![在这里插入图片描述]()
定义:
![在这里插入图片描述]()
2.3 推导、分析树与语法树
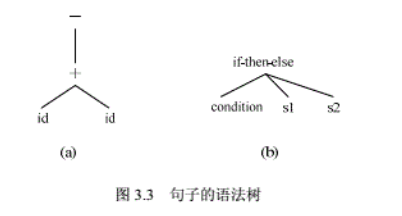
- 分析树(具体语法树)
![在这里插入图片描述]()
- 语法树(抽象语法树)
![在这里插入图片描述]()
(a)是上述分析树对应的语法树
(b)是条件语句if condition then s1 else s2 的语法树
2.4 二义性与二义性的消除
2.4.1 二义性
(1)一个句型有多于一颗分析树,仅与文法和句型有关,与采用的推导方法无关
(2)造成二义性的原因,是文法中缺少对文法符号优先级和结合性的规定
2.4.2二义性的消除
为文法的符号规定适当的优先级和结合性
- 两种方法
- 改写二义文法为非二义文法
- 对二义施加限制,规定优先级和结合性
1) 改写二义文法为非二义文法
- 栗子:改写二义文法G3.2为非二义文法G3.4
<!--文法G3.4-->
E->E+T|T
T->T*F|F
F->(E)|-F|id
用文法G3.4对id+id*id重新推导
最左推导:
E => E+T => T+T => F+T => id+T => id+T*F
=> id+F*F => id+id*F => id+id*id
最右推导
E => E+T => E+T*F => F+T*id => E+F*id => E+id*id
=> T+id*id => F+id*id => id+id*id
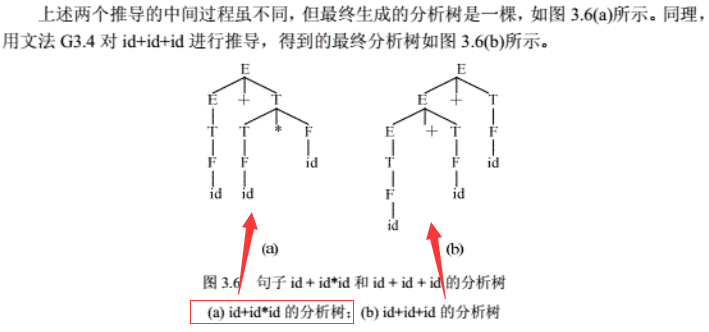
结论:
- 由于新引入的非终结符限制每一步直接推导均有唯一选择,使得同一句子仅有一颗分析树。
- 最终产生的分析树与推导方法无关,而仅与文法的描述有关。
- 引入新的非终结符,使得直接推导的步骤数增加,分析树的高度增高,从而分析效率降低。
- 越接近S的A与a,优先级越低。
- 对具有递归定义性质的A产生式A->αAβ,若a∈β(A在a的左边),则a具有左结合性质;若a∈α(A在a的右边),则a具有右结合性质;例如E->E+T中E在+的左边,则+具有左结合性质;若产生式形如E->T+E,则+具有右结合性质。
2)为文法符号规定优先级和结合性
在二义文法G3.2中,只要分别为+、*和-规定正确的优先级和结合性,就会使得分析任何一个句子时仅能得到一颗分析树。
3. 语言与文法
程序设计语言的结构均可以用文法来描述
(1)文法给出了精确的、易于理解的语言结构的说明
(2)以文法为基础的语言,以便于加入新的或修改、删除旧的语言结构
(3)有些类别的文法,可以自动生成高效的分析器
3.1 正规式与上下文无关文法
CFG:所有的产生式左边只有一个非终结符
- 正规式到CFG的转换
推论:正规式所描述的语言结构均可以用CFG来描述,反之不一定
步骤:- 构造正规式的NFA
- 若0为初态,则A0为开始符号
- 对于move(i,a)=j,引入产生式Ai->aAj
- 对于move(i,ε)=j,引入产生式Ai->Aj
- 若i是终态,则引入产生式Ai->ε
栗子:r=(a|b)*abb的CFG
<!--文法G3.6-->
A0->aA0|bA0|aA1
A1->bA2
A2->bA3
A3->ε
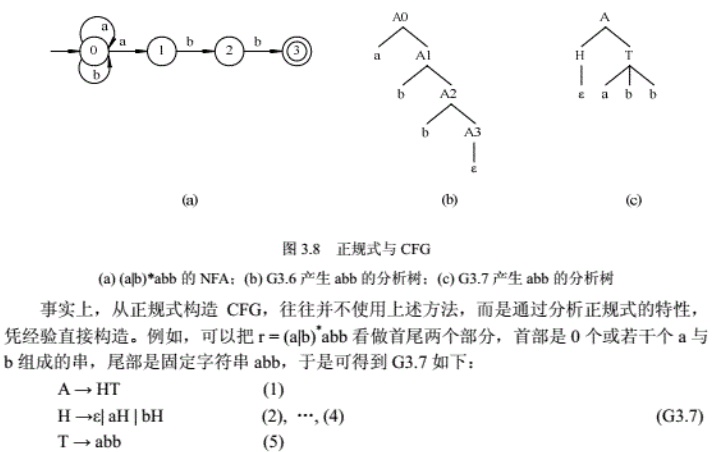
- 为什么用正规式而不用CFG描述程序设计语言的词法
采用正规式:- 词法规则简单,用正规式描述已足够
- 正规式的表示比CFG更直观、简洁,易于理解
- 有限自动机的构造比下推自动机简单,且分析效率高
- 区分词法和语法,为编译器前端的模块划分提供方便
3.2 上下文有关文法
第一个产生式左边有不止一个符号
所有产生式的左部长度都小于等于右部长度
3.3 形式化语言与自动机
定义:若文法G=(N,T,P,S)的每个产生式α->β中,均有α∈(N∪T)*,且至少含有一个非终结符,β∈(N∪T)*,则称G为0型文法。
对0型文法施加以下第i条限制,即可得到i型文法
(1)G的任何产生式α->β(S->ε除外)均满足|α|<=|β|(|x|表示x中文法符号的个数)
(2)G的任何产生式形如A->β,其中A∈N,β∈(N∪T)*。
(3)G的任何产生式形如A->a,或者A->aB(或者A->Ba),其中A,B∈N,a∈T*。
| 文法 | 产生式 | 语言 | 自动机 |
|---|---|---|---|
| 0型(短语)文法 | α->β | 0型语言(短语结构语言,递归可枚举集) | 图灵机 |
| 1型文法(CSG) | 限制1 | 1型语言(CSL) | 线性界线自动机 |
| 2型文法(CFG) | 限制2 | 2型语言(CFL) | 下推自动机 |
| 3型(正规)文法 | 限制3 | 3型语言(正规语言,正规集) | 有限自动机 |
4. 自上而下语法分析
4.1 自上而下分析的一般方法
基本思想:对于任何一个输入序列,从文法的开始符号开始,进行最左推导,直到得到一个合法句子或者发现一个非法结构。在推导过程中试图用一切可能的方法,自上而下、从左到右为输入序列建立分析树。
存在的问题:
- 左因子:有相同前缀,例如A->αβ1|αβ2
- 左递归:陷入死循环而使分析无法进行下去,例如A->Aα
4.2 消除左递归

-
消除文法的直接左递归
对于产生式A->Aα|β,可以用非左递归的A->βA’和A’->αA’|ε取代
![在这里插入图片描述]()
-
消除文法的左递归
例如:S=>Aa=>Sda
![在这里插入图片描述]()
4.3 提取左因子
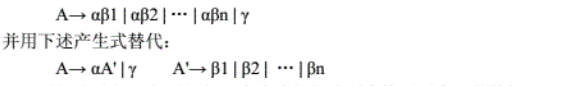
当一个文法中既有左递归又含左因子时,一般的做法时先消除左递归。
4.4 递归下降分析
- 写程序
- 递归下降分析是直接以程序的方式模拟产生式产生语言的过程。
- 基本思想:为每一个非终结符构造一个子程序,每一个子程序的过程体中按该产生式的候选项分情况展开,遇到终结符匹配,而遇到非终结符就调用相应非终结符的子程序。
限制:不能有公共左因子和左递归 - 称为:递归下降子程序
- 构造过程:
(1)构造文法的状态转换图并且简化
(2)将状态图转化为EBNF表示
(3)从EBNF构造子程序
4.5 预测分析器
预测分析器:又称为非递归预测分析器或者表驱动的预测分析器,数学模型是下推自动机
组成:预测分析表、一个符号栈和一个驱动器
4.5.1 非递归预测分析器的工作模式
- 下推自动机与格局
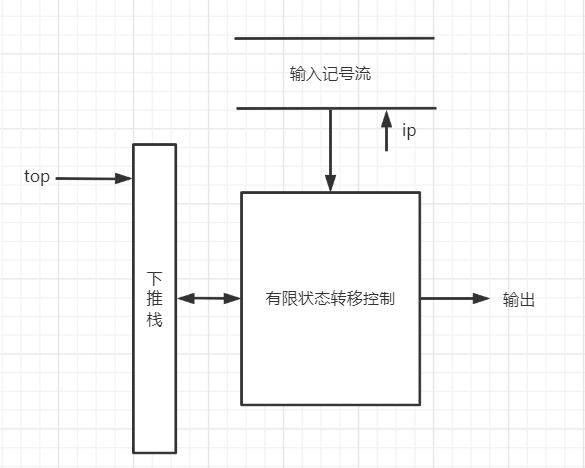
下推自动机模型
只读头:ip指向当前输入
下推栈:top指向栈顶
有限状态转移控制:
![在这里插入图片描述]()
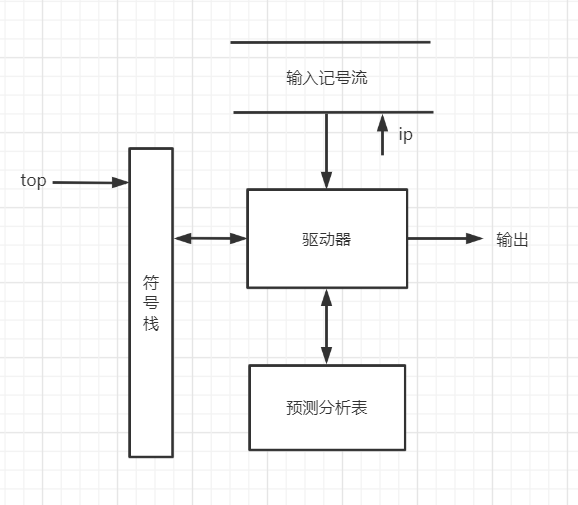
预测分析器:
下推栈:符号栈,用来存放终结符与非终结符
有限状态转移控制:预测分析表+驱动器
![在这里插入图片描述]()
下推自动机的工作模式:是一种放幻灯的方式,此处的每张“幻灯片”称为一个格局。
格局是一个三元组:(站内容,剩余输入,改变格局的动作)
分析是从某个初始格局开始的,经过一系列的格局变化,最终到达接受格局,表明分析成功;或者到达出错格局,表明发现一个语法错误。
开始格局:全部输入序列
接受格局:剩余输入应该为空 - 预测分析表中的内容与改变格局的动作
四种改变格局的动作:- 匹配终结符:若栈顶和当前输入终结符相等且不是结束标志#,则分析器弹出栈顶符号(pop),输入指针指向下一个终结符(next(ip))。
- 展开终结符:栈顶符号是非终结符X,当前输入时终结符a,驱动器访问分析表M[X,a];若M[X,a]时X产生式的某候选项,则用此候选项取代栈顶的X。
- 报告分析成功:栈顶和当前输入符号均为#,分析成功并结束。
- 报告出错:
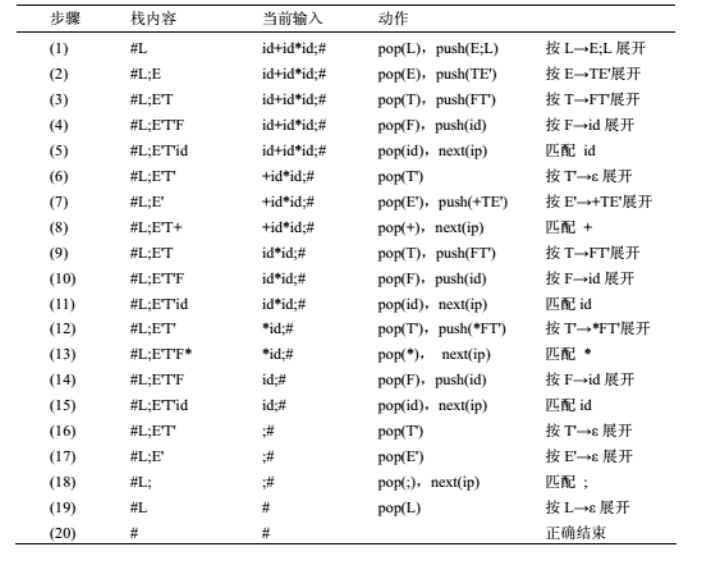
栗子:表3.2给出了文法G3.9’的预测分析表。用算法3.4作为驱动器,表3.2作为分析表,分析输入序列id+id*id;的过程如下。


4.5.2 构造预测分析表
-
计算FIRST集合
![在这里插入图片描述]()
-
计算所有非终结符的FOLLOW集合
![在这里插入图片描述]()
栗子:
![在这里插入图片描述]()
4.5.3 LL(1)文法
一个文法G被称为时LL(1)文法,当且仅当为它构造的预测分析表中不含有多重定义的条目时。由此分析表所组成的分析器被称为LL(1)分析器,它所分析的语言被称为LL(1)语言。
- 第一个L表示从左到右扫描输入序列
- 第二个L表示产生最左推导
- 1表示在确定分析器的每一步动作时间向前看一个终结符
5. 自下而上语法分析
5.1 自下而上分析的基本方法
- 规范归约与“剪句柄”
![在这里插入图片描述]()
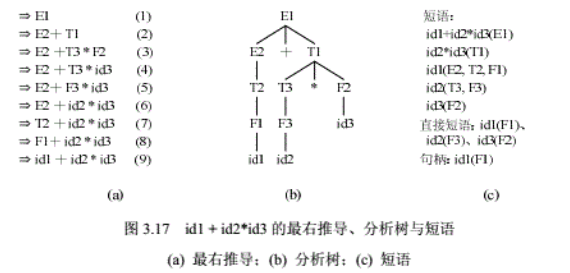
- 短语:以非终结符为根的子树中所有从左到右排列的叶子
- 直接短语:只有父子关系的树中所有从左到右排列的叶子(树高为2)
- 句柄:最左边父子关系树中所有从左到右排列的叶子(句柄是唯一的)
![在这里插入图片描述]()
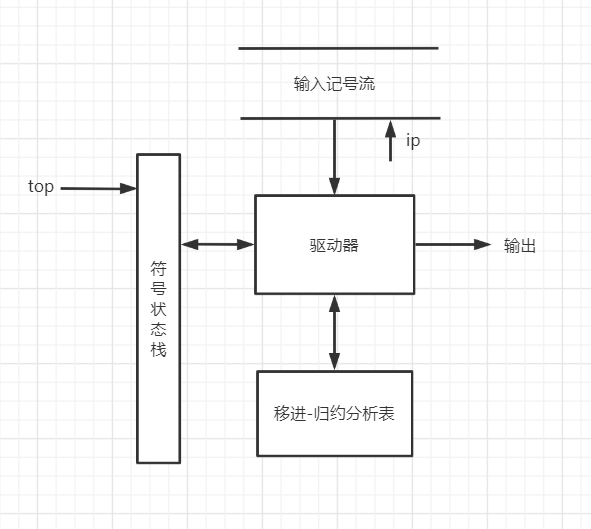
- 移进——归约分析器的工作模式
![在这里插入图片描述]()
- 改变格局的动作:
- 移进(shift):把当前输入中的下一个终结符移进栈
- 归约(reduce):句柄在栈顶已形成,用适当产生式左部代替句柄
- 接受(accept):宣告分析成功
- 报错(error):发现语法错误,调用语法恢复例程
5.2 LR分析
5.2.1 LR分析与LR文法
LR分析的核心是LR分析表和驱动器
LR分析表由两部分组成:一部分是动作表,另一部分是转移表
- 栗子:
-
文法:
![在这里插入图片描述]()
-
移进——归约分析表:
![在这里插入图片描述]()
-
解释:
s:表示当前状态
a:表示终结符
A:表示非终结符
action[s,a]:指示当前栈顶状态为s和输入终结符为a时应进行的下一动作
goto[s,A]:指示当前栈顶为s和非终结符A时的下一状态转移 -
分析过程
![在这里插入图片描述]()
![在这里插入图片描述]()
-
5.2.2 构造SLR(1) 分析器
SLR(1)分析器简称SLR分析器,S表示Simple 简单的意思
- 构造SLR分析表的基本思想:首先构造一个可以识别文法G中所有活前缀的DFA,然后根据DFA和简单的向前看信息构造SLR分析表
- 活前缀与LR(0)项目
活前缀:出现在移进——归约分析器栈中的右句型的前缀
LR(0)项目:简称项目,在它右部的某个位置上,右一个点“.”。对于A->ε,它仅有一个项目A->. 。 - 拓广文法与识别活前缀的DFA
![在这里插入图片描述]()
![在这里插入图片描述]()
![在这里插入图片描述]()
![在这里插入图片描述]()
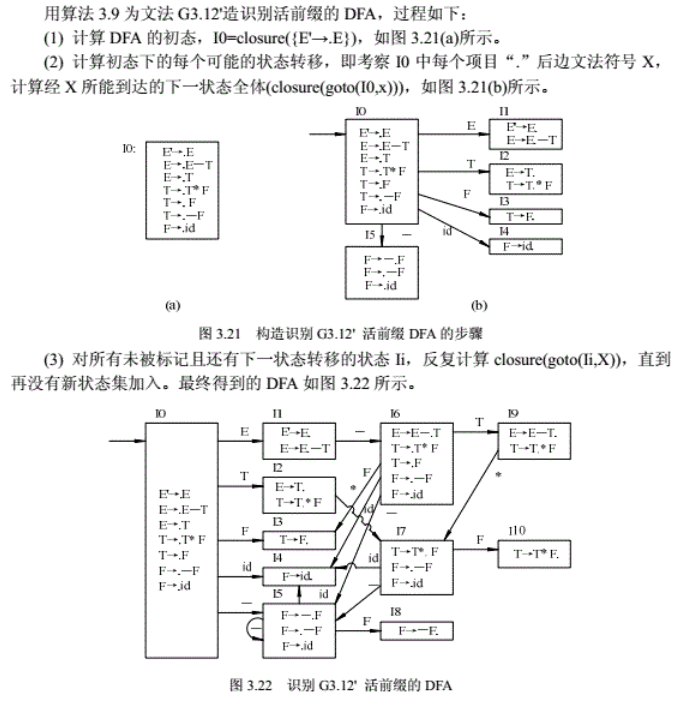
栗子:
![在这里插入图片描述]()
- 识别活前缀
![在这里插入图片描述]()

















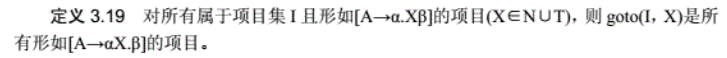

 浙公网安备 33010602011771号
浙公网安备 33010602011771号