编译原理笔记（四）之静态语义分析

静态语义分析

• 1. 语法制导翻译简介
• • 1.1 语法与语义
  • 1.2 属性与语义规则
  • 1.3 语义规则的两种形式
  • 1.4 LR分析翻译方案的设计
  • 1.5 递归下降分析翻译方案的设计
• 2. 中间代码简介
• • 2.1 后缀式
  • 2.2 三地址码
  • • 2.2.1 三元式表示
    • 2.2.2 三元式的语法制导翻译
    • 2.2.3 四元式表示
    • 2.2.4 四元式的语法制导翻译
  • 2.3 图形表示
  • • 2.3.1 树作为中间代码
    • 2.3.2 树的语法制导翻译
    • 2.3.3 树的优化表示—DAG
    • 2.3.4 树与其他中间代码的关系
• 3. 符号表简介
• • 3.1 符号表条目
  • 3.2 构成名字的字符串
  • 3.3 名字的作用域
  • 3.4 线性表
  • 3.5 散列表
• 4. 声明语句的翻译
• • 4.1 变量的声明
  • 4.2 数组变量的声明
  • 4.3 过程的定义与声明
• 5. 简单算术表达式与赋值句
• • 5.1 简单变量的语法制导翻译
  • 5.2 变量的类型转换
• 6. 数组元素的引用
• 7. 布尔表达式
• 8. 控制语句

静态语义分析的两个作用：检查出源程序中的静态语义错误和将语义正确的语句翻译成中间代码

1. 语法制导翻译简介

1.1 语法与语义

• 语义揭示了程序本身的涵义、施加于语言结构上的限制或者要执行的动作。
• 语义分析的双重作用：
  • 检查语言结构的语义是否正确，即是否结构正确的句子所表示的意思也合法。
  • 执行所规定的语义动作，如表达式的求值、符号表的填写、中间代码的生成等。
• 语义分析方法：语法制导翻译，基本思想是将语言结构的语义以属性的形式赋予代表此结构的文法符号，而属性的计算以语义规则的形式赋予由文法符号组成的产生式。

1.2 属性与语义规则

• 定义：对于产生式A→a，其中α是由文法符号X1X2…Xn组成的序列，它的语义规则可以表示为式(4.1)所示关于属性的函数:
  b := f(cl, c2，…-", ck)
  语义规则中的属性存在下述性质与关系:
  (1)若b是A的属性，c1, c2，…, ck 是α中文法符号的属性或者A的其他属性，则称b是A的综合属性。
  (2)若b是α中某文法符号Xi的属性，c1, c2，…, ck是A的属性或者是α中其他文法符号的属性,则称b是Xi的继承属性。
  (3)称式(4.1)中属性b依赖于属性c1, c2，…, ck。
  (4)若语义规则的形式如下述式(4.2)，则可将其想像为产生式左部文法符号A的一个虚拟属性，属性之间的依赖关系在虚拟属性上依然存在:
  f(cl, c2，…, ck)
  文法符号属性的抽象表示采用点加标识符(.属性)的方法

• 继承属性：自上而下，包括兄弟

• 综合属性：自下而上，包括自身

1.3 语义规则的两种形式

1. 语法制导定义：用抽象的属性和运算符号表示的语义规则（算法）
2. 翻译方案：用具体属性和运算表示的语义规则（程序）

1.4 LR分析翻译方案的设计

可以把语法制导翻译看做语法分析的扩充

1. 扩充LR分析器的功能
2. 扩充分析栈（新增加一个语义栈）

1.5 递归下降分析翻译方案的设计

从上到下构造一棵树
对虚拟分析树的一次深度优先遍历

2. 中间代码简介

• 中间代码实际上应起分隔编译器前端与后端分水岭的作用
• 目的：便于编译器的开发移植和代码的优化
• 特性：1. 便于语法制导翻译 2. 既与机器指令的结构相近，又与具体机器无关
• 主要形式：树（最基本）、后缀式、三地址码（最常用，采用四元式形式）等

2.1 后缀式

• 也叫逆波兰表示，典型特征是操作数在前，操作符紧跟其后。
• 例如：a+bc的后缀式表示为abc+，而（3+5）*（8+2）的后缀式为35+82*
• 优点：没有括号且便于计算

2.2 三地址码

• 三地址码是由不超过三个地址组成的一个运算：
• 形式：
  result：=arg1 op arg2 或者result：=op arg1 或者op arg1
• arg1和arg2用于存放运算对象
• result用于存放运算结果
• 三地址码是最终生成目标代码的理性中间代码形式

三地址码的种类

序号	三地址码	四元式
(1)	x :=y op z	(op, y,z,x)
(2)	x :=op y	(op, y, ,x)
(3)	x := y	(:=,y, ,x)
(4)	goto L	(j, , ,L)
(5)	if x goto L	(jnz, x, ,L)
(6)	if x relop y goto L	(jrelop, x, y, L)
(7)	param x	(param, , ,x)
(8)	call P,n	(call, n, , P)
(9)	return y	(return, , ,y)
(10)	x :=y[i]	(=[], y[i], ,x)
(11)	x[i]:=y	([]=, y, ,x[i])
(12)	x := &y	(=&, y , , x)
(13)	x :=*y	(=*, y , , x)
(14)	*x :=y	(*=, y , , x)

2.2.1 三元式表示

表示:
(i)(op, arg1, arg2)
代表的计算是：
(i):=arg1 op arg2
即arg1和arg2分别作为左右操作数进行op运算，运算结果存放在三元式的编号(i)中。

2.2.2 三元式的语法制导翻译

为文法符号和产生式设计如下的属性和语义函数：

1. 属性.code：表示三元式代码，指示标识符的存储单元或三元式表中的序号。
2. 属性.name：给出标识符的名字。
3. 函数 trip( op，arg1，arg2)：生成一个三元式，返回三元式的序号。若运算是一元的，如E一-E1，则arg2可以为空。
4. 函数entry(id.name)：根据标识符id.name查找符号表并返回它在符号表中的位置或存储位置。为了直观，三元式中仍以标识符自身的名字表示。

对于简单赋值句的求值，三元式语法制导翻译如下:

(1) A->id :=E 	{A.code := trip( :=，entry(id.name)，E.code ) }
(2) E->E1+E2 	{E.code := trip(+，E1.code，E2.code ) }
(3) E->E1*E2	{E.code := trip(*，E1.code，E2.code ) }
(4)	E->(E1 )	{E.code := E1.code }
(5) E->E1		{E.code := trip( @，E1.code，)}
(6)	E->id 		{E.code := entry(id.name)}

2.2.3 四元式表示

• 形式：
  （op，arg1，arg2，result）
• 所表示的计算：
  result:=arg1 op arg2
• 运行结果存放在result(临时变量)中
• 四元式和三元式的唯一区别是将由序号所表示的运算结果改为了由临时变量来表示。

2.2.4 四元式的语法制导翻译

对于简单赋值句的求值，四元式语法制导翻译如下:

(1)A→id:=E	{A.code := newtemp; emit(:=，cntry(id.name)，E.code, A.code)}(2)E→E1+E2 	{E.code := newtemp; emit( +，E1.code，E2.code, E.code)}
(3)E→E1*E2 	{E.code := newtemp; emit(*,E1.code，E2.code,E.code)}
(4)E→(E1)	{E.code := E1.code }
(5)E→-E1	{E.code := newtemp; emit( @，E1.code，, E.code) }
(6)E→id		{E.code := entry(id.name)}
/*此处，属性.code表示存放运算结果的变量;
	   函数 newtemp表示返回一个新的临时变量，如T1、T2等;
	   过程emit( op, arg1 , arg2, result)生成一个四元式,若运算是一元的,如E→-E1，则arg2可以为空。*/

栗子：赋值句x:=a+bc 可由一组四元式表示如下:
(， b, c, T1)
(+，a，T1, T2)
(:=，x，T2, T3)

2.3 图形表示

2.3.1 树作为中间代码

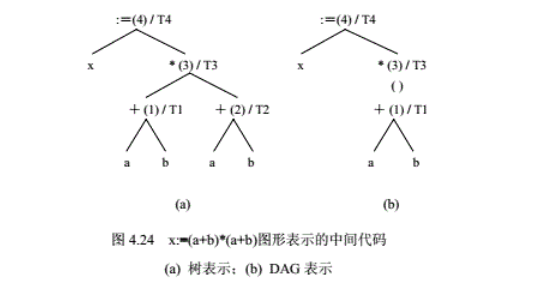
2.3.2 树的语法制导翻译

对简单赋值句的求值进行语法制导翻译如下:

(1)A→id :=E		{A.nptr := mknode( :=，mkleaf(entry(id.name))，E.nptr ) }
(2)E→El+E2	 	{ E.nptr := mknode( +，E1.nptr，E2.nptr ) }
(3)E→E1 * E2 	{E.nptr := mknode(*，E1.nptr，E2.nptr ) }
(4)E→(E1)		{E.nptr := E1.nptr }
(5)E→-E1		{E.nptr := mknode( @，E1.nptr, )}
(6) E→ id		{E.nptr := mkleaf(entry((id.name))}

其中，属性.nptr是指向树节点的指针;
函数 mknode(op，nptr1，nptr2) 生成一个根或内部节点，节点的数据是op，左右孩子分别是nptr1和 nptr2所指向的子树，若仅有一个孩子，则nptr2为空:函数mkleaf(node)生成一个叶子节点。

2.3.3 树的优化表示—DAG

如果若干个节点有完全相同的孩子，则这些节点可以指向同一个孩子(如图4.24(b)所示)，形成一个有向无环图(DAG)。DAG与树的唯一区别是多个父亲可以共享同一个孩子，从而达到资源(运算、代码等)共享的目的。

2.3.4 树与其他中间代码的关系

对树进行深度优先的后序遍历，得到的线性序列就是后缀式，或者说后缀式是树的一个线性化序列；而对于每棵父子关系的子树，父亲节点作为操作符，两个孩子节点作为操作数，恰好组成一个三元式，且父亲节点的序号成为三元式的序号。为每个三元式序号赋一个临时变量，就不难将三元式转换为四元式。

3. 符号表简介

符号表示连接声明与引用的桥梁。

3.1 符号表条目

• 条目：每个声明的名字在符号表中占据一栏
  条目的名字可以不唯一，格式无需统一
• C语言构造的符号表中，一个名字的组合关键字至少包括三项：名字+作用域+类型

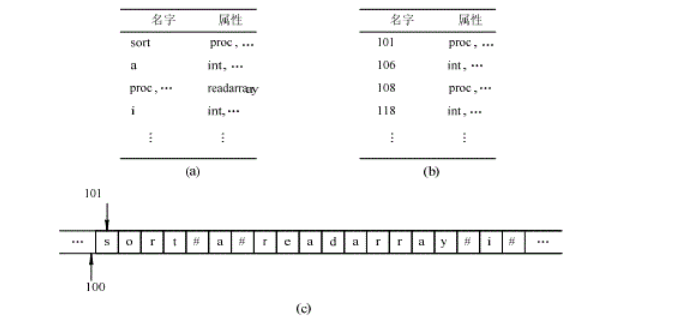
3.2 构成名字的字符串

直接存储方式：直接将构成名字的字符串存放在符号表中的方式（a）
间接存储方式：将构成名字的字符串统一存放在一个大的连续空间中（c）,字符串与字符串之间用特殊的分隔符隔开，而在符号表的条目，仅存放指向该字符串首字符的指针即可（b）和（c）

3.3 名字的作用域

划分范围的两种方式：并列和嵌套

1. 静态作用域原则：编译时就可以确定名字的作用域，也可以说，仅从静态读程序就可确定名字的作用域。
2. 最近嵌套原则：

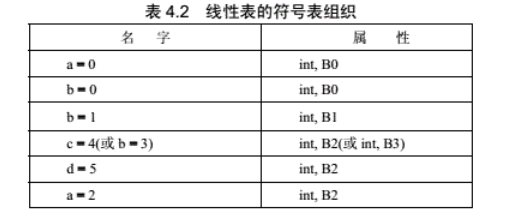
3.4 线性表

最简单和最容易实现符号表的数据结构是线性表。
可以将线性表表示为一个数组，也可以表示为一个单链表。
为了正确反映名字的作用域，线性表应具有栈的性质，即符号的加入和删除均在线性表的一端进行。

3.5 散列表

1. 构成
   为了提高符号表的查找效率,可以将线性表化整为零，分成m个子线性表，简称子表。构造一个散列函数，使符号表中元素均匀地散布在这 m个子表中。散列表的结构如图4.26所示，m个子表的表头构成一个表头数组，它以散列函数的值(hash 值)为下标，每个子表的组织与上述线性表相同。具有相同hash 值的节点被散列在相同子表中，连接子表的链被称为散列链。如果散列均匀，则时间复杂度会降到原线性表的1/m。
   

2. 散列表的操作
   （1）查找
   （2）插入
   （3）删除

4. 声明语句的翻译

4.1 变量的声明

1. 变量的类型定义与声明
   类型定义：为编译器提供存储空间大小的信息
   变量声明：为变量分配存储空间
2. 变量声明的语法制导翻译

4.2 数组变量的声明

符号表提供四个域（name，type，offset，width）
分辨表示名字、类型、相对存储位置、变量的宽度

1. 静态数组的内情向量
   内情向量是一种数据结构
   n维整型数组声明：array [d1] of array [d2] of … array[dn] of integer

n：表示数组的维度
c：计算数组元素在被分配的数组存储空间中的相对位置所需的一个常数
offset：数组的首地址偏移量
di：每维的成员个数
type：数组元素的类型

4.3 过程的定义与声明

• 规格说明：或过程头，过程的界面
• 过程体：过程所要完成操作的具体实现
• 函数：有返回值的过程
• 主程序：可以被认为是操作系统调用的过程
• 三种形式：过程定义、过程声明和过程调用

1. 左值与右值

左值是地址，右值是指，也可以说左值是容器，右值是内容。

2. 参数传递
   形参
   实参
   值调用
   引用调用
   复写-恢复
   换名调用

3. 作用域信息的保存
   （1）过程的作用域
   （2）符号表中的作用域信息

5. 简单算术表达式与赋值句

5.1 简单变量的语法制导翻译

5.2 变量的类型转换

强制：整型量转换为实型量
T：=itr E 将E从整型变为实型，结果存放在T中
T：=rti E 将E从实型变为整型，结果存放在T中

6. 数组元素的引用

数组元素的地址计算

7. 布尔表达式

1. 逻辑运算
2. 控制语句转移的控制条件

8. 控制语句

1. 无条件转移语句
2. 条件转移语句
3. 循环语句
4. 分支语句