常用的数据结构
1. 线性表
1.1 概念
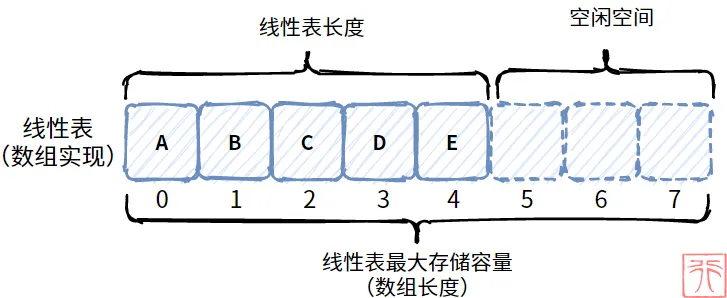
线性表:一个线性表是n个具有相同特性的数据元素的有限序列;(由顺序表或者链式表示)常见的线性表有:栈、队列、字符串、数组、链表、双向链表、循环队列;
线性表中数据元素之间的关系是一对一的关系,即除了第一个和最后一个数据元素之外,其他数据元素都是首尾相接的(注意,这句话只适用于大部分线性表,而不是全部。比如,循环链表逻辑层次上也是一种线性表(存储上属于链式存储,但是把最后一个数据元素的尾指针指向了首位结点))
1.2 特征
- 集合中必存在
唯一的一个“第一元素” - 集合中必存在
唯一的“最后元素“ - 除最后一个元素之外,均有
唯一的后继 - 除第一个元素之外,均有
唯一的前驱
2. 线性数据结构
2.1 数组
2.1.1 概念
数组是一种线性结构,而且在物理内存中也占据着一块连续空间。
2.1.2 优点
访问数据简单(适合随机访问,因为是通过索引访问,时间复杂度为O(1),例如:arr[1] )
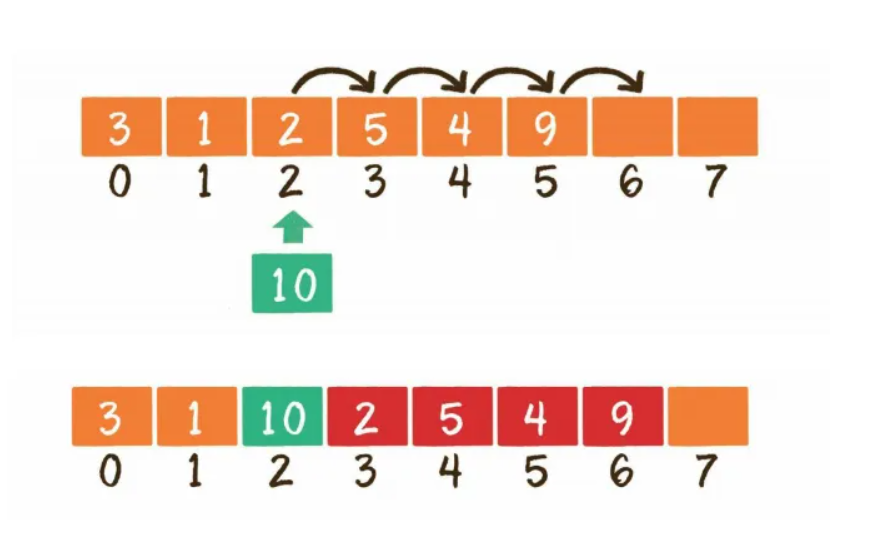
2.1.3 缺点
添加和删除数据比较耗时,添加删除元素的时候需要移动其后的元素,时间复杂度为O(N)
2.1.4 使用场景
频繁查询,对存储空间要求不大,很少增加和删除的情况
2.2 链表
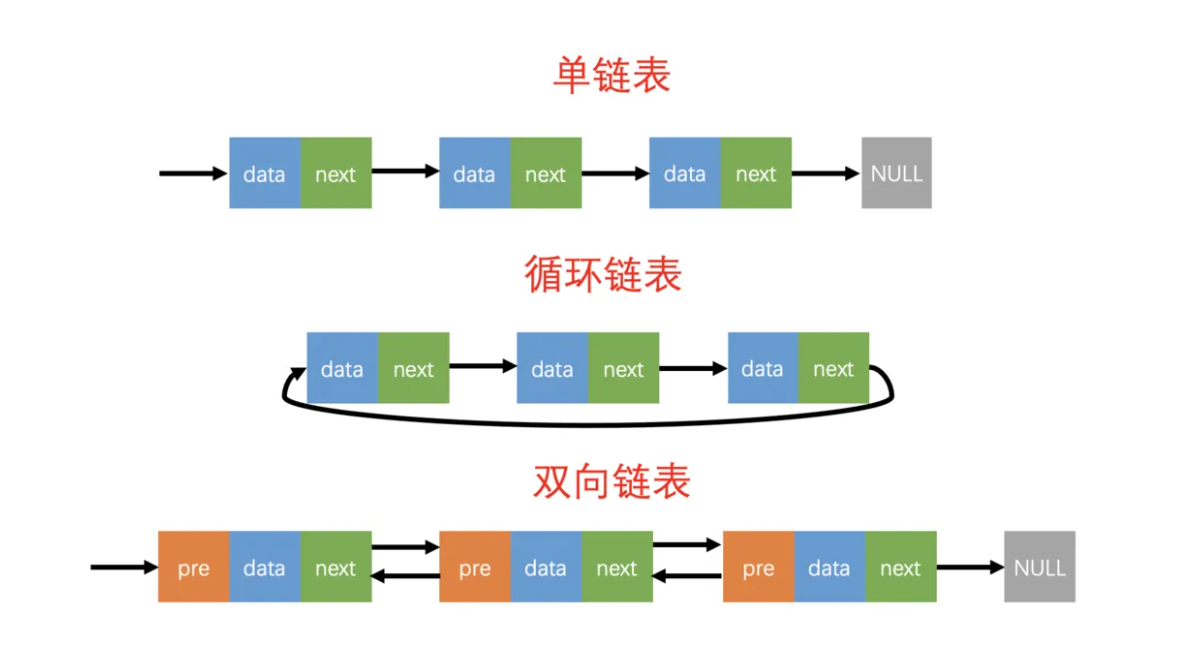
2.2.1 概念
链表是物理存储单元上非连续的、非顺序的存储结构,数据元素的逻辑顺序是通过链表的指针地址实现,每个元素包含两个节点,一个是存储元素的数据域(内存空间),另一个指向下一个节点地址的指针域。
2.2.2 优点
数据添加和删除方便
2.2.3 缺点
访问比较耗费时间
2.2.4 使用场景
数据量较小,需要频繁增加、删除操作的场景
2.3 栈
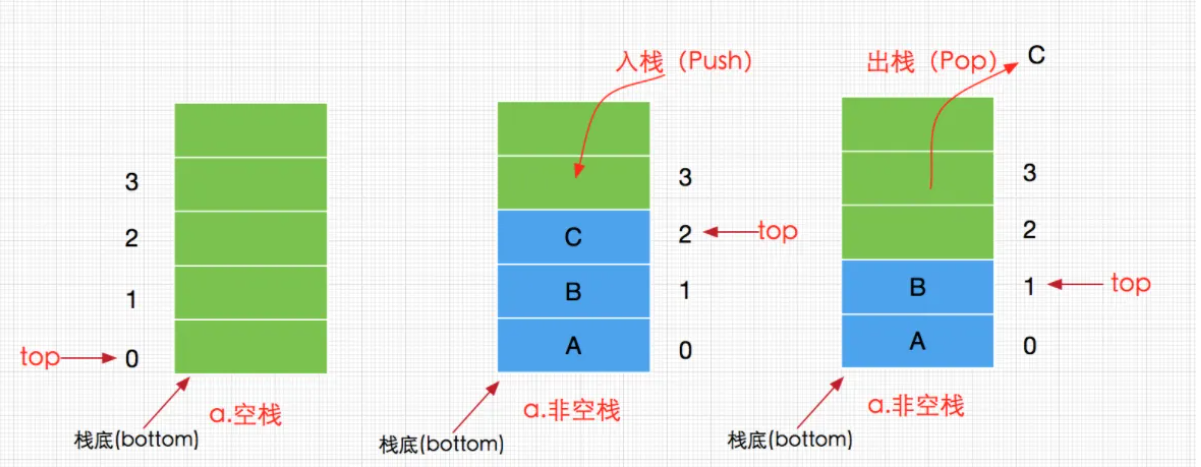
2.3.1 概念
栈也是一种数据呈线性排列的数据结构,不过在这种结构中,我们只能访问最新添加的数据。从栈顶放入元素的操作叫做入栈,取出元素的操作叫做出栈。
2.3.2 特点
后进先出(Last In First Out,简称LIFO)
2.4 队列
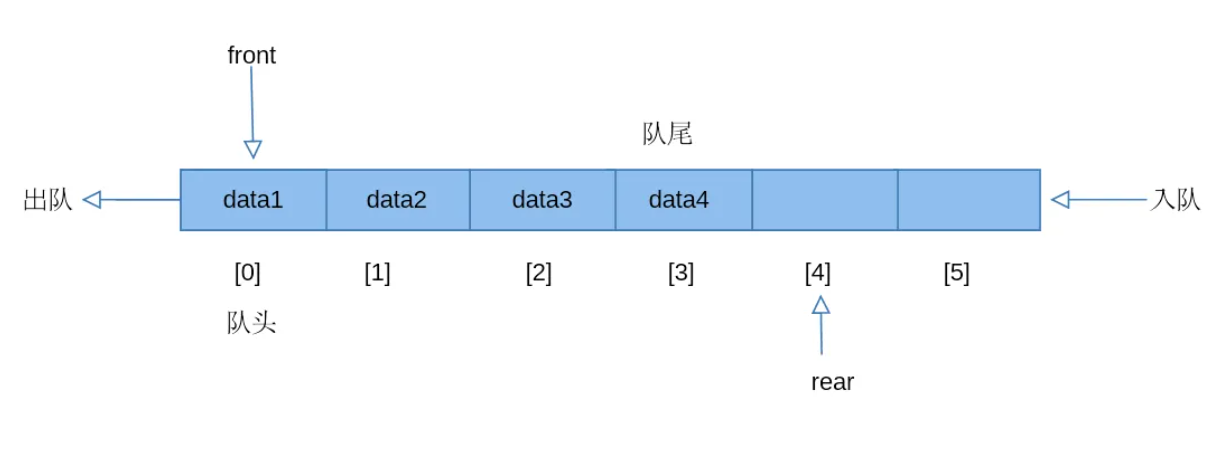
2.4.1 概念
队列中的添加和删除数据的操作分别是在两端进行的。队列可以在一端添加元素,在另一端取出
元素。
2.4.2 特点
先进先出(First In First Out,简称FIFO)
3. 非线性数据结构
3.1 树
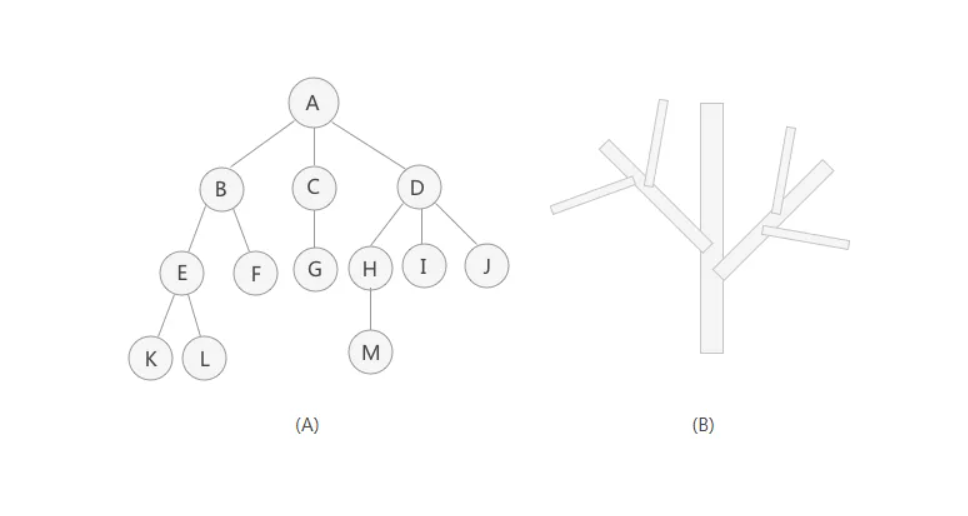
3.1.1 概念
它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一颗倒挂的树,也就是说它是根朝上,而叶朝下的。
3.1.2 特点
- 每个节点由零个或多个子节点
- 没有父节点的节点成为根节点
- 没有一个非根节点有且只有一个父节点
- 除了根节点外,每个子节点可以分为多个不相交的子树
3.1.3 二叉树
- 每个节点最多有两颗子节点
- 左子树和右子树是有顺序的,次序不能颠倒
- 及时某节点只有一个子树,也要区分左右子树
3.1.4 BTree
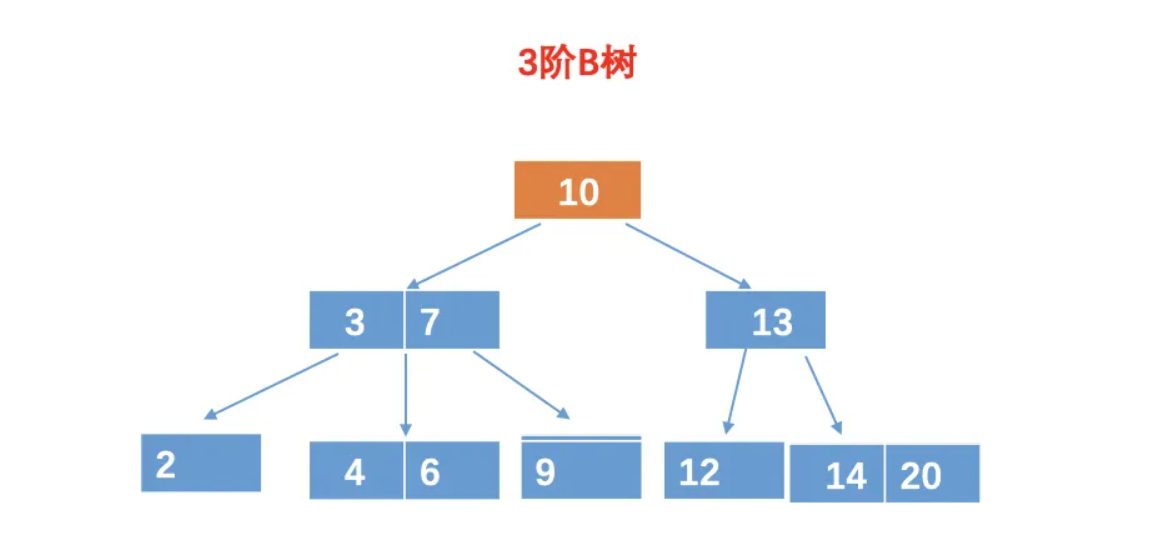
3.1.4.1 概念
BTree是一种平衡的多路搜索树,它维护有序数据并允许以对数时间进行搜索,顺序访问,插入和删除。B树是二叉搜索树的一般化,因为节点可以有两个以上的子节点。与其他自平衡二进制搜索树不同,B树非常适合读取和写入相对较大的数据块(如光盘)的存储系统,它通常用于数据库和文件系统。
3.1.4.2 特征
一颗m叉(阶)的BTree特性如下:
- 树中每个节点最多包含m个孩子
- 除根节点与叶子节点外,每个节点至少有 [ ceil ( m/2 ) ] 个孩子
- 若根节点不是叶子节点,则至少有两个孩子
- 所有的叶子节点都在同一层
- 每个非叶子节点由 n 个 key 与 n+1 个指针组成,其中 [ ceil ( m/2 ) - 1 ] <= n <= m - 1
3.1.5 B+Tree
3.1.5.1 概念
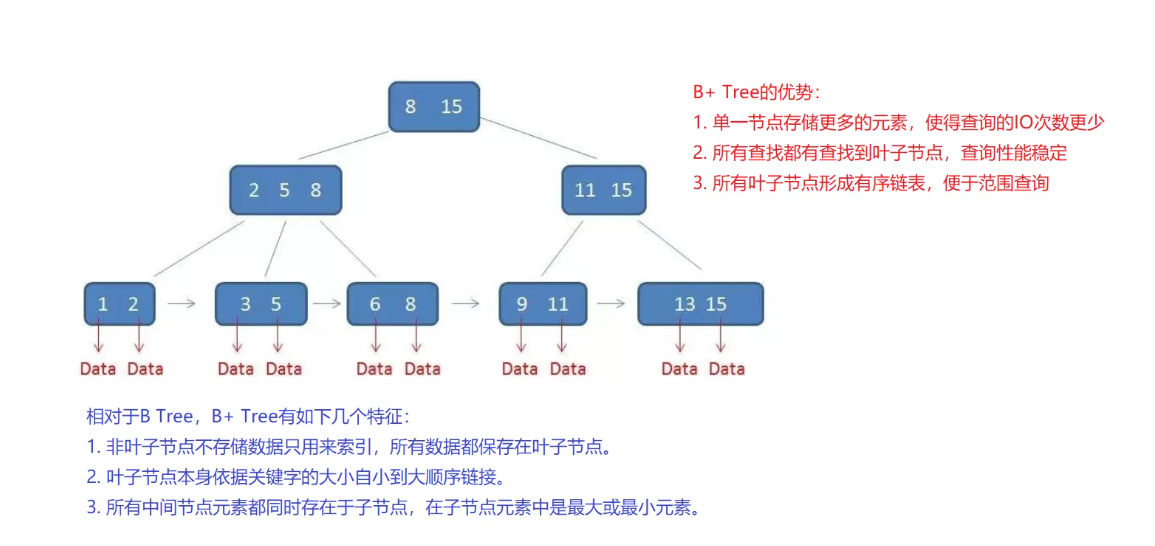
B+Tree是BTree 的一个变种,最大的区别是B+Tree内部节点不保存数据,只保存索引信息,所有数据都保存在叶子节点。
3.1.5.2 特征
- 每个元素不保存数据,只用来索引,所有数据都保存在叶子节点
- 所有叶子节点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子节点本身依关键字的大小自小而大顺序链接
- 所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素
- 不但节点之间含有重复元素,而且叶子节点还用指针链接在一起
3.1.5.3 B + Tree的优势
-
B+树的磁盘读写代价很低
B+树的内部节点并没有指向关键字具体信息的指针。因此其内部节点相对B树更小,如果把所有同一内部节点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
-
B+树查询效率更加稳定
由于非终结点并不是最终指向文件内容的节点,而只是叶子节点中关键字的索引。所以任何关键字的查找必须走一条从根节点到叶子节点的路。所有关键字查询的路径长度相同,导致每一个数据的查询相率相当。
-
B+树便于范围查询(最重要的原因,范围查找是数据库的常态)
B树在提高了IO性能的同时并没有解决元素遍历的效率低下的问题,正式为了解决这个问题,B+树应用而生。B+树只需要去遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常繁琐的,而B树不支持这样的操作或者说是效率太低。
3.2. 堆
3.2.1 概念
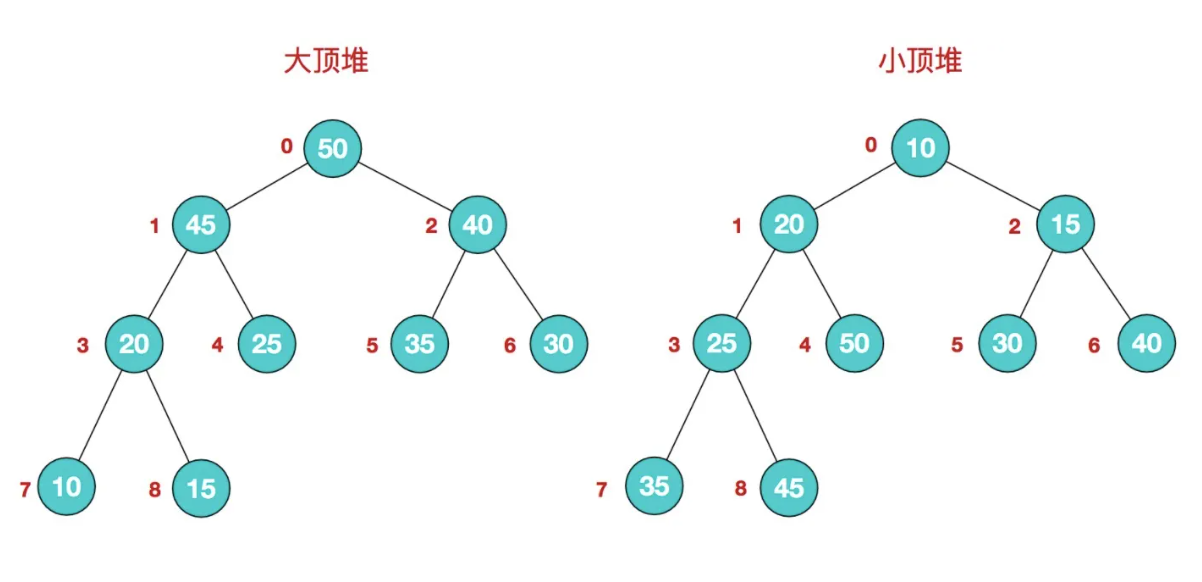
堆是一种图的树形结构,被用于实现“优先队列”。优先队列是一种数据结构,可以自由添加数据,但取出数据时要从最小值开始按顺序取出。在堆的树形结构中,各个顶点被称为“结点”(node),数据就存储在这些结点中,
3.2.2 特点
- 每个节点最多有两个子节点
- 排列顺序必须从上到下,同一行从左到右
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 存放数据时,一般会把新数据放在最下面一行靠左的位置。如果最下面一行没有多余空间时,就再往下另起一行,并把数据添加到这一行的最左端
3.3 哈希表
3.3.1 概念
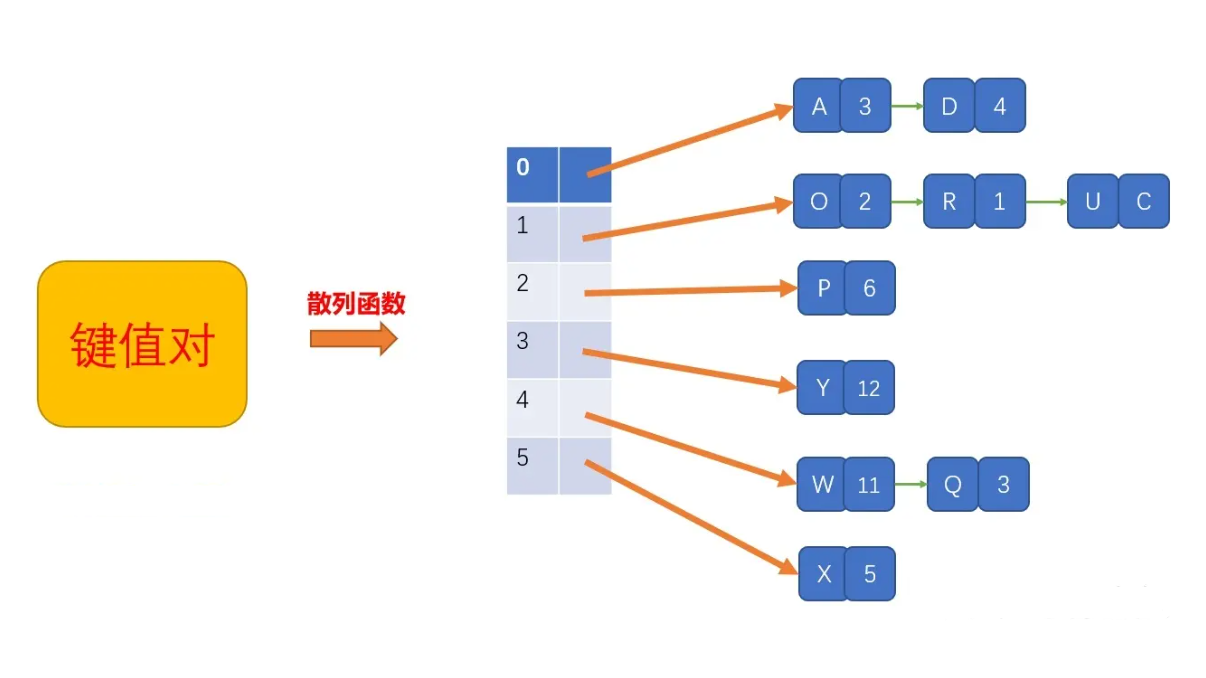
哈希表,也叫散列表,是根据关键码和值(key和value)直接进行访问的数据结构,通过key和value来映射集合中的一个位置,这样就可以很快找到集合中的对应元素。
3.3.2 特点
- 可以利用哈希函数快速访问到数组的目标数据,如果发生哈希冲突,就是用链表进行存储。
- 如果数组的空间太小,使用哈希表的时候就容易发生冲突,线性查找的使用频率也就会更高;反过来,如果数组的空间太大,就会出现很多空箱子,造成内存的浪费。因此,给数组设定合适的空间非常重要。
- 在存储的过程中,如果发生冲突,可以利用链表在已有数据的后面插入新数据来解决冲突。这种方法被称为“链地址法”。除了链地址法以外,还有几种解决冲突的方法。其中,应用较为广泛的是“开放地址法”。
3.4 图
3.4.1 概念
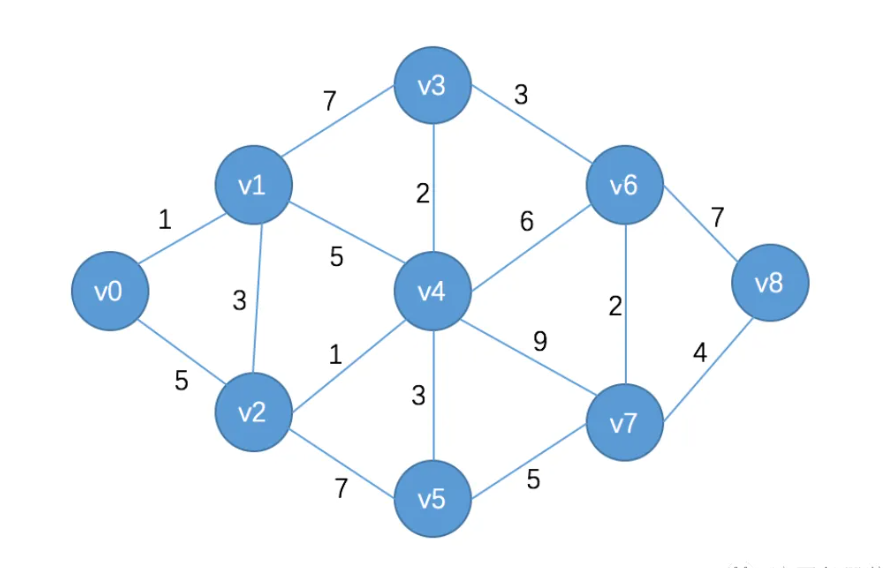
图是由节点的有穷集合V和边的集合E组成。其中,为了与树形结构加以区别,在图结构中常常将节点成为顶点,边是顶点的有序偶对,若两个节点之间存在一条边,就表示这两个顶点具有相邻的关系。按照顶点指向的方向可以分为无向图和有向图;
3.4.2 无向图
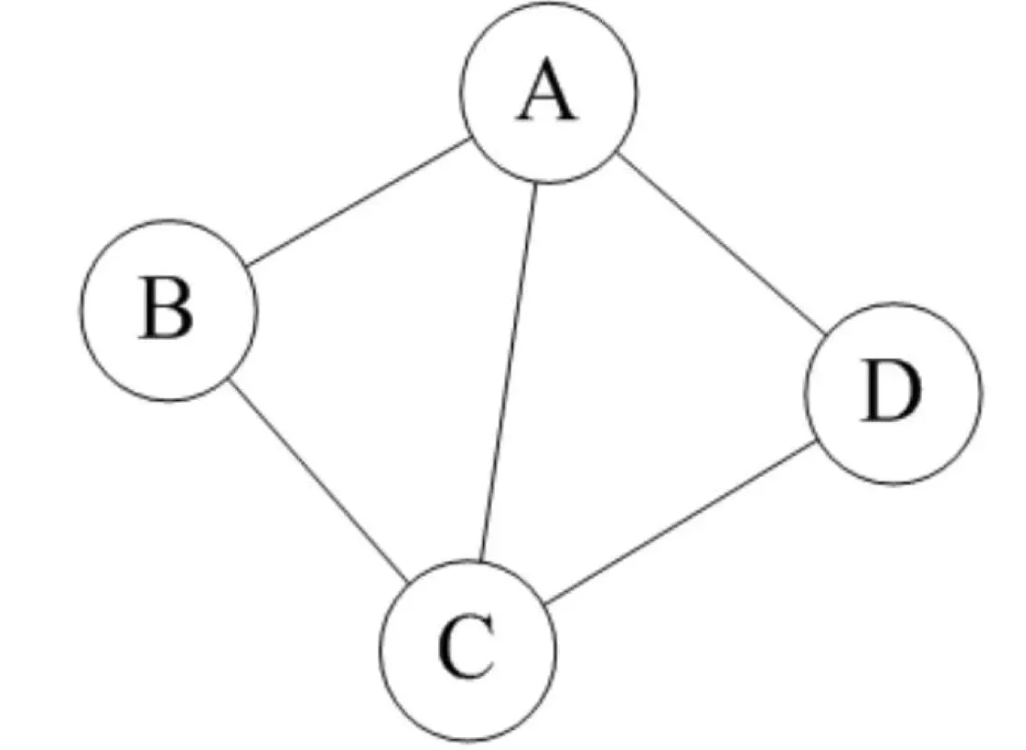
3.4.3 有向图
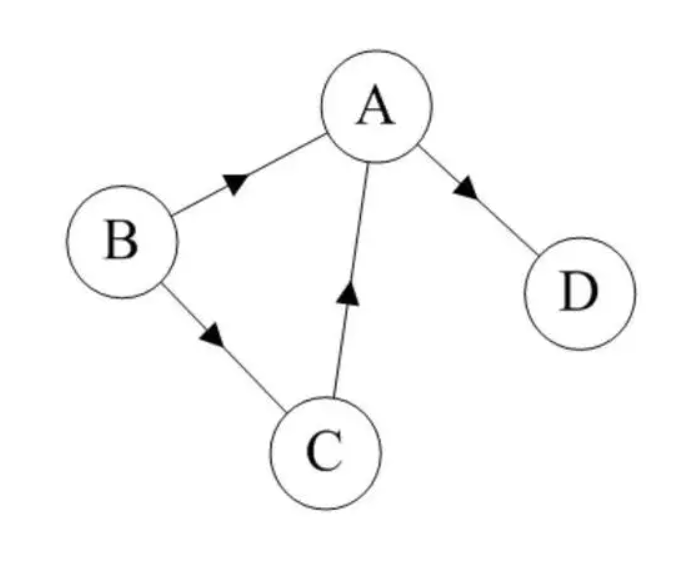



 浙公网安备 33010602011771号
浙公网安备 33010602011771号