1-3次作业总结

一、前三次作业总结

（1）第一次作业：第一次作业比较简单，主要完成一些小功能，让我们熟悉一些输入输出方式方法的使用，没有太大的算法上的需求。

（2）第二次作业：第二次作业主要是字符串函数的运用，第一，三题主要考察字符的提取，算法上比较简单，没有过多的设计。第二题与奇偶校验有关，也要提取字符。测试点比较多，需要考录的情况也比较多，总体来说思路其实是比较简单的，但我还是有些点没有过去。

（3）第三次作业：主要是点线型的几何计算。三个题目由易到难，分别从点到先，再到三角形进行计算。需要考虑到三角形由线组成，而线由点组成，可以运用JAVA类的思想，设置点、线、三角形类，将会减少后面反复编写相似的代码，减少代码的长度。

二、设计与分析

第一次作业有8个小题，都比较基础，细心做就没什么问题。

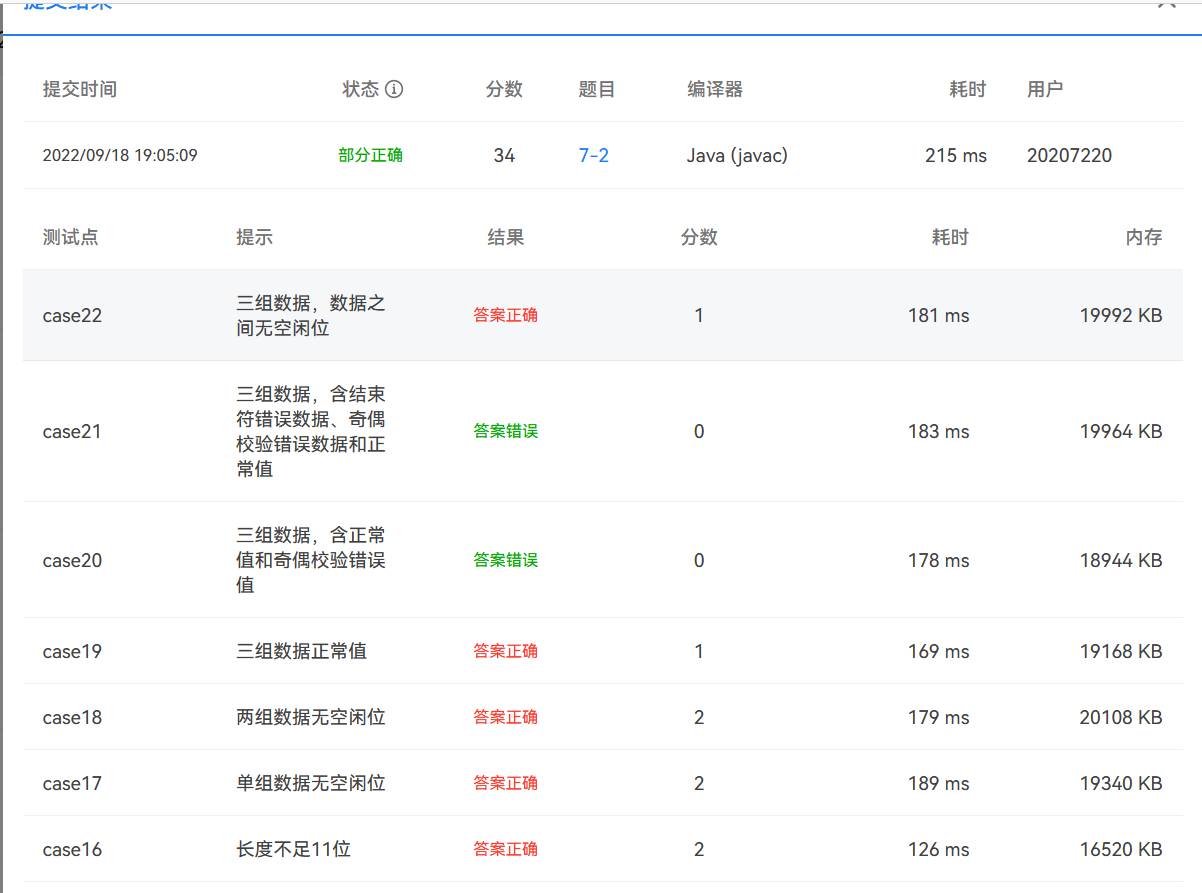
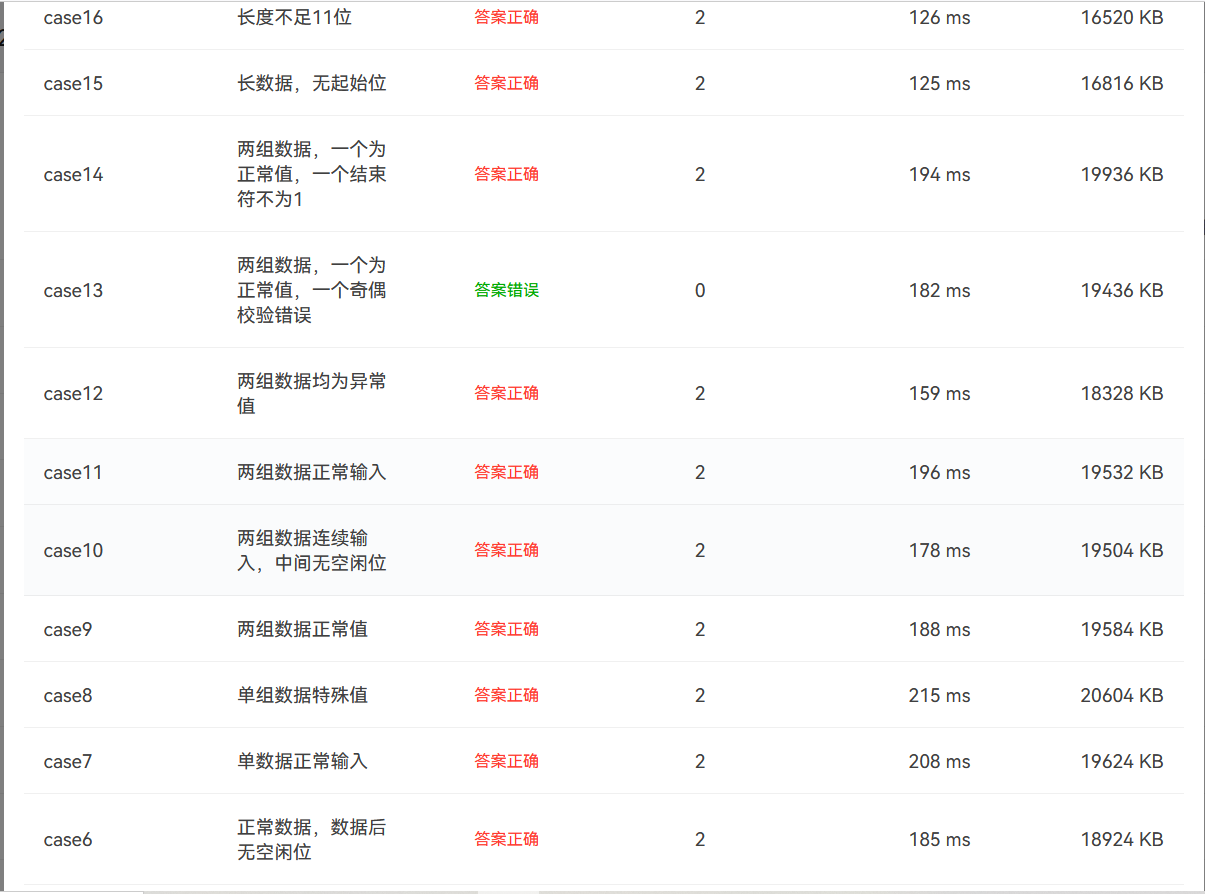
第二次作业的第2题题目比较长，测试点比较多，有很多坑。本题题目我没有使用类，只用了一个类写完的，利用if-else语句实现多种情况。最后给出的测试例题都正确但测试点仍然有些没过。用sourcemonitor测试圈复杂度。显然圈复杂度高了，不利于维护和更新。

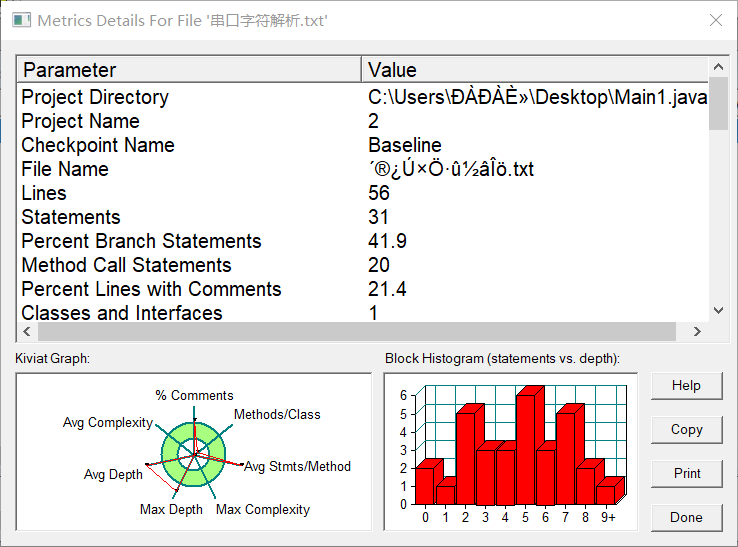
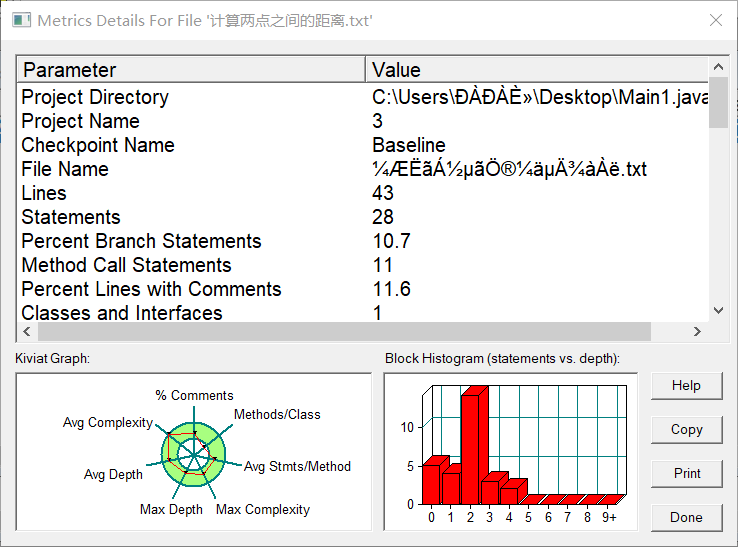
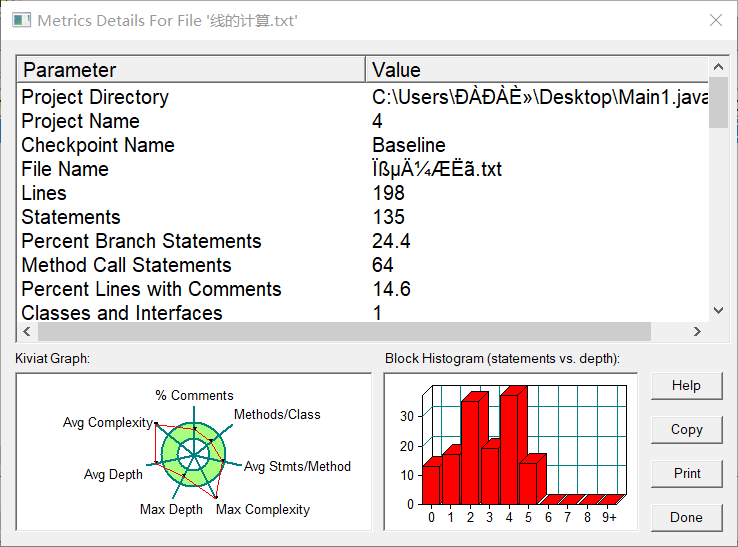
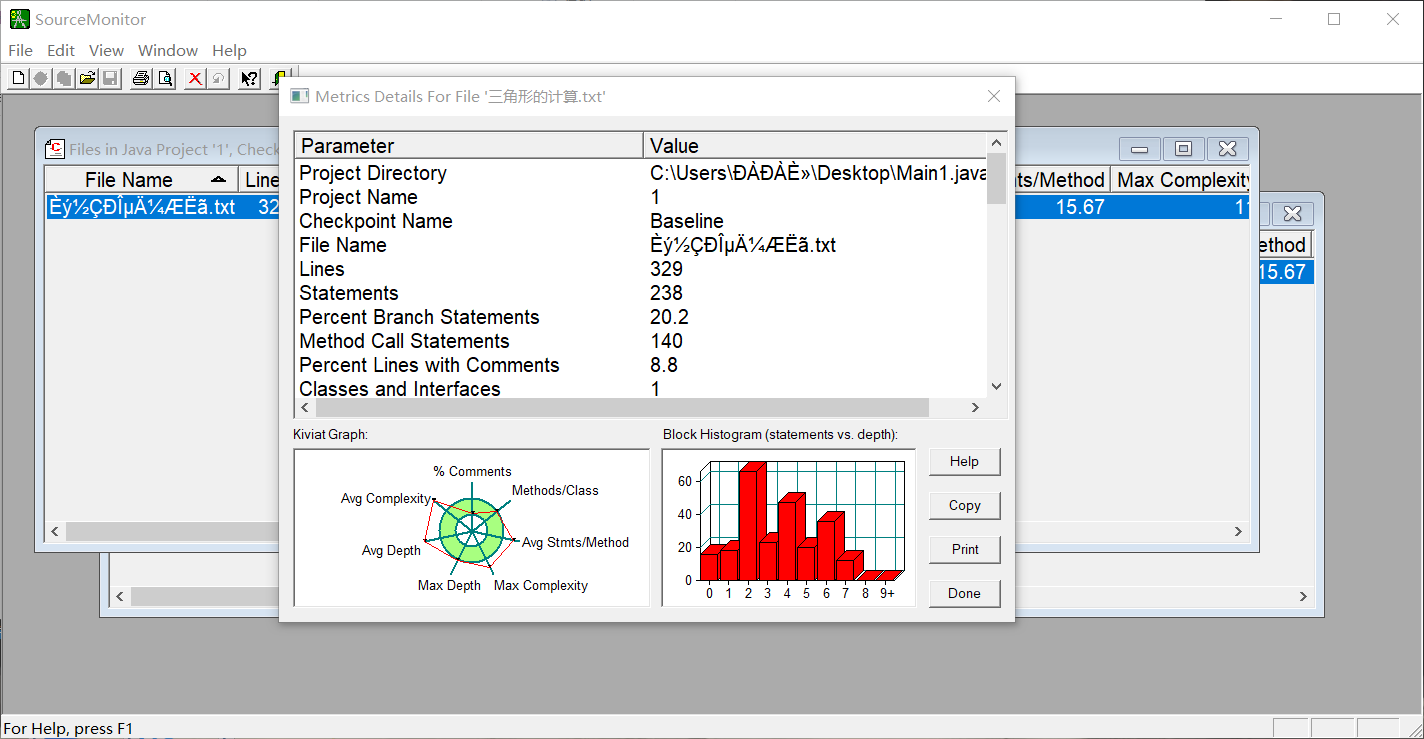
第三次作业的3个题目都比较长，要完成的测试点比较多。在设计代码时准备用一个点，线，三角形三个类来写。第二个题目可以用到第一个题目中两点之间的距离的算法，及引用点类里面的方法，第三个题目中的代码可以用到点、线的类方法。最后，第一题用类写没有问题可以通过所有测试点，但到后面两个，算法设计起来比较复杂，尤其是第三个代码计算直线与三角形的交点个数和坐标的算法不会写，测试点基本都没过。代码测试图如下：第一个代码的圈复杂度比较低，方法与类的设计比较合理，较易维护；第2,3题的代码写了将近两三百行，圈复杂度很高！由图可看出最大深度，复杂度都比较高，维护更新的费用也相对比较高。

 1 import java.util.Scanner;
 2 public class Main{
 3     public static void main(String args[]){
 4         Scanner input = new Scanner(System.in);
 5         String s = input.nextLine();
 6         //输入格式
 7         String[] n1 = s.split(",|[ ]");
 8         for(int i=0;i<n1.length;i++){
 9             if(!n1[i].matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$")){
10                 System.out.print("Wrong Format");
11                 return;
12             }
13         }
14         //长度不为2
15         String[] dianji = s.split(" ");
16         if(dianji.length!=2){
17             System.out.println("wrong number of points");
18             return;
19         }
20         //转换为数值
21         double a = new Double(n1[0]);
22         double b = new Double(n1[1]);
23         double c = new Double(n1[2]);
24         double d = new Double(n1[3]);
25         //创建对象点a,b
26         Dian a1 = new Dian();
27         Dian a2 = new Dian();
28         a1.setxy(a,b);
29         a2.setxy(c,d);
30         System.out.print(a1.distance(a2));
31     }
32 }
33 //点
34 class Dian{
35     double x,y;
36     public void setxy(double x,double y){
37         this.x=x;
38         this.y=y;
39     }
40     public double distance(Dian b1){
41         return Math.sqrt((this.x-b1.x)*(this.x-b1.x)+(this.y-b1.y)*(this.y-b1.y));
42     }
43 }

第一题比较简单，写一个简单的点类即可，但其实这里的点累没有写全。

  1 import java.util.Scanner;
  2 public class Main{
  3     public static void main(String args[]){
  4         Scanner input = new Scanner(System.in);
  5         String s = input.nextLine();
  6         //判断输入格式正误
  7         String[] n = s.split("[ ,]");
  8         for(int i=0;i<n.length;i++){
  9             if(i==0&&!n[0].matches("^[1-5]:[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$")){
 10                 System.out.print("Wrong Format");
 11                 return;
 12             }
 13             else if(i>0&&!n[i].matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$")){
 14                 System.out.print("Wrong Format");
 15                 return;
 16             }
 17         }
 18         String[] point = s.split(",| |:");
 19         String[] n1 = s.split(" ");
 20         if(point[0].equals("2")||point[0].equals("1")||point[0].equals("3")){
 21             if(n1.length!=3)
 22                 System.out.print("wrong number of points");
 23             else{
 24                 double a = new Double(point[1]);
 25                 double b = new Double(point[2]);
 26                 double c = new Double(point[3]);
 27                 double d = new Double(point[4]);
 28                 double e = new Double(point[5]);
 29                 double f = new Double(point[6]);
 30                 Dian p1 = new Dian();
 31                 Dian p2 = new Dian();
 32                 Dian p3 = new Dian();
 33                 p1.setxy(a,b);
 34                 p2.setxy(c,d);
 35                 p3.setxy(e,f);
 36                 Xian l1 = new Xian();
 37                 Xian l2 = new Xian();
 38                 Xian l3 = new Xian();
 39                 l1.setXY(p1,p2);
 40                 l2.setXY(p1,p3);
 41                 l3.setXY(p2,p3);
 42                 double ax = l1.getXianLength();
 43                 double bx = l2.getXianLength();
 44                 double cx = l3.getXianLength();
 45                 if(p1.pointsCoincide(p2)==0||p1.pointsCoincide(p3)==0||p2.pointsCoincide(p3)==0)//构成直线的两点重合
 46                     System.out.print("data error");
 47                 else{
 48                   if(ax+bx==cx||ax+cx==bx||bx+cx==ax){//共线
 49                     System.out.print("data error");
 50                       return ;
 51                   }
 52                   else{
 53                   //选项1
 54                    if(point[0].equals("1")){
 55                       //等腰和等边
 56                        if(p1.distance(p2)==p1.distance(p3)||p1.distance(p2)==p2.distance(p3)||p1.distance(p3)==p2.distance(p3)){
 57                             if(p1.distance(p2)==p2.distance(p3)&&p1.distance(p2)==p1.distance(p3))
 58                                 System.out.print("true true");
 59                             else 
 60                                 System.out.print("true false");
 61                        }
 62                        else
 63                            System.out.print("false false");
 64                  }
 65                   //选项2
 66                   else if(point[0].equals("2")){
 67                       double C0 = l1.getXianLength()+l2.getXianLength()+l3.getXianLength();
 68                       double leng1 = Math.abs((p3.y-p2.y)*p1.x+(p2.x-p3.x)*p1.y+p3.x*p2.y-p3.y*p2.x)/Math.sqrt((p3.y-p2.y)*(p3.y-p2.y)+(p3.x-p2.x)*(p3.x-p2.x));
 69                       double area = 0.5*leng1*l3.getXianLength();
 70                       double x0 = (p1.x+p2.x+p3.x)/3;
 71                       double y0 = (p1.y+p2.y+p3.y)/3;
 72                       if((C0*1000000)%10 != 0){
 73                           String CC = String.format("%.6f",C0);
 74                           System.out.print(CC);
 75                       }
 76                       else 
 77                           System.out.print(C0);
 78                       if((area*1000000)%10 != 0){
 79                           String Area = String.format("%.6f",area);
 80                           System.out.print(" "+Area);
 81                       }
 82                       else 
 83                           System.out.print(" "+area);
 84                       if((x0*1000000)%10 != 0){
 85                           String X0 = String.format("%.6f",x0);
 86                           System.out.print(" "+X0+",");
 87                       }
 88                       else 
 89                           System.out.print(" "+x0+",");
 90                       if((y0*1000000)%10 != 0){
 91                           String Y0 = String.format("%.6f",y0);
 92                           System.out.print(Y0);
 93                       }
 94                       else 
 95                           System.out.print(y0);
 96                   }
 97                   //选项3
 98                   else{
 99                       
100                       double a0 = Math.sqrt((p2.x-p3.x)*(p2.x-p3.x)+(p2.y-p3.y)*(p2.y-p3.y));
101                       double b0 = Math.sqrt((p1.x-p3.x)*(p1.x-p3.x)+(p1.y-p3.y)*(p1.y-p3.y));
102                       double c0 = Math.sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
103                       double A = Math.toDegrees(Math.acos((a0*a0-b0*b0-c0*c0)/(-2*b0*c0)));
104                       double B = Math.toDegrees(Math.acos((b0*b0-a0*a0-c0*c0)/(-2*a0*c0)));
105                       double C = Math.toDegrees(Math.acos((c0*c0-b0*b0-a0*a0)/(-2*b0*a0)));
106                       if(A==90||B==90||C==90)
107                           System.out.print("false true false");
108                       else if(A>90||B>90||C>90)
109                           System.out.print("true false false");
110                       else if(A<90&&B<90&&C<90)
111                           System.out.print("false false true");
112                    }
113                   }
114               }
115             }
116         }
117         //选项四
118         else if(point[0].equals("4")){
119             if(n1.length!=5)
120             System.out.print("wrong number of points");
121             else{
122                 double a = new Double(point[1]);
123                 double b = new Double(point[2]);
124                 double c = new Double(point[3]);
125                 double d = new Double(point[4]);
126                 double e = new Double(point[5]);
127                 double f = new Double(point[6]);
128                 double g = new Double(point[7]);
129                 double h = new Double(point[8]);
130                 double p = new Double(point[9]);
131                 double q = new Double(point[10]);
132                 Dian p1 = new Dian();
133                 Dian p2 = new Dian();
134                 Dian p3 = new Dian();
135                 Dian p4 = new Dian();
136                 Dian p5 = new Dian();
137                 p1.setxy(a,b);
138                 p2.setxy(c,d);
139                 p3.setxy(e,f);
140                 p4.setxy(g,h);
141                 p5.setxy(p,q);
142                 Xian l1 = new Xian();
143                 Xian l2 = new Xian();
144                 Xian l3 = new Xian();
145                 Xian l4 = new Xian();
146                 l1.setXY(p1,p2);
147                 l2.setXY(p3,p4);
148                 l3.setXY(p3,p5);
149                 l4.setXY(p4,p5);
150                 double a0 = l2.getXianLength();
151                 double b0 = l3.getXianLength();
152                 double c0 = l4.getXianLength();
153                 if(p1.pointsCoincide(p2)==0||p4.pointsCoincide(p3)==0||p5.pointsCoincide(p4)==0||p3.pointsCoincide(p5)==0)//构成直线的两点重合
154                     System.out.print("points coincide");
155                 else if(l2.Slope()==l3.Slope()||l3.Slope()==l4.Slope()||l2.Slope()==l4.Slope()||(p3.x==p4.x&&p3.x==p5.x))
156                     System.out.print("data error");
157                 else{
158                     int flag = 0;
159                     int lp1=0,lp2 = 0,lp3 = 0;
160                     double x0=0,y0=0;
161                     double xi=0,yi=0;
162                     double xj=0,yj=0;
163                     
164                     if(l2.isParallelOrNot(l1) == -1){
165                         //double x0=0;
166                           // double y0=0;
167                            x0 = ((l2.a1.x-l2.a2.x)*(l1.a1.y*l1.a2.x-l1.a1.x*l1.a2.y)-(l1.a1.x-l1.a2.x)*(l2.a1.y*l2.a2.x-l2.a1.x*l2.a2.y))/((l1.a1.y-l1.a2.y)*(l2.a1.x-l2.a2.x)-(l2.a1.y-l2.a2.y)*(l1.a1.x-l1.a2.x));
168                            y0 = ((l2.a1.y-l2.a2.y)*(l1.a1.y*l1.a2.x-l1.a1.x*l1.a2.y)-(l1.a1.y-l1.a2.y)*(l2.a1.y*l2.a2.x-l2.a1.x*l2.a2.y))/((l1.a1.y-l1.a2.y)*(l2.a1.x-l2.a2.x)-(l2.a1.y-l2.a2.y)*(l1.a1.x-l1.a2.x));
169                         
170                         if((x0>=Math.min(l2.a1.x,l2.a2.x)&&x0<=Math.max(l2.a1.x,l2.a2.x))||(y0>=Math.min(l2.a1.y,l2.a2.y)&&y0<=Math.max(l2.a1.y,l2.a2.y))){
171                             flag = flag+1;
172                             lp1 = 1;
173                         }
174                     }
175                     else if(l2.isParallelOrNot(l1) == 1){
176                         double leng = Math.abs((p4.y-p3.y)*p1.x+(p3.x-p4.x)*p1.y+p4.x*p3.y-p4.y*p3.x)/Math.sqrt((p4.y-p3.y)*(p4.y-p3.y)+(p4.x-p3.x)*(p4.x-p3.x));
177                         if(leng==0){
178                             System.out.print("The point is on the edge of the triangle");
179                             return;
180                         }
181                     }
182                     if(l3.isParallelOrNot(l1) == -1){
183                         //double xi=0;
184                         //double yi=0;
185                         xi = ((l3.a1.x-l3.a2.x)*(l1.a1.y*l1.a2.x-l1.a1.x*l1.a2.y)-(l1.a1.x-l1.a2.x)*(l3.a1.y*l3.a2.x-l3.a1.x*l3.a2.y))/((l1.a1.y-l1.a2.y)*(l3.a1.x-l3.a2.x)-(l3.a1.y-l3.a2.y)*(l1.a1.x-l1.a2.x));
186                         yi = ((l3.a1.y-l3.a2.y)*(l1.a1.y*l1.a2.x-l1.a1.x*l1.a2.y)-(l1.a1.y-l1.a2.y)*(l3.a1.y*l3.a2.x-l3.a1.x*l3.a2.y))/((l1.a1.y-l1.a2.y)*(l3.a1.x-l3.a2.x)-(l3.a1.y-l3.a2.y)*(l1.a1.x-l1.a2.x));
187                         
188                         if((xi>=Math.min(l3.a1.x,l3.a2.x)&&xi<=Math.max(l3.a1.x,l3.a2.x))||(yi>=Math.min(l3.a1.y,l3.a2.y)&&yi<=Math.max(l3.a1.y,l3.a2.y)))
189                             if(xi!=x0&&yi!=y0){
190                             lp2 = 1;
191                             flag = flag+1;
192                         }
193                     }
194                     else if(l3.isParallelOrNot(l1) == 1){
195                         double leng = Math.abs((p5.y-p3.y)*p1.x+(p3.x-p5.x)*p1.y+p5.x*p3.y-p5.y*p3.x)/Math.sqrt((p5.y-p3.y)*(p5.y-p3.y)+(p5.x-p3.x)*(p5.x-p3.x));
196                         if(leng==0){
197                             System.out.print("The point is on the edge of the triangle");
198                             return;
199                         }
200                     }
201                     if(l4.isParallelOrNot(l1) == -1){
202                         //double xj=0;
203                         //double yj=0;
204                         xj = ((l4.a1.x-l4.a2.x)*(l1.a1.y*l1.a2.x-l1.a1.x*l1.a2.y)-(l1.a1.x-l1.a2.x)*(l4.a1.y*l4.a2.x-l4.a1.x*l4.a2.y))/((l1.a1.y-l1.a2.y)*(l4.a1.x-l4.a2.x)-(l4.a1.y-l4.a2.y)*(l1.a1.x-l1.a2.x));
205                         yj = ((l4.a1.y-l4.a2.y)*(l1.a1.y*l1.a2.x-l1.a1.x*l1.a2.y)-(l1.a1.y-l1.a2.y)*(l4.a1.y*l4.a2.x-l4.a1.x*l4.a2.y))/((l1.a1.y-l1.a2.y)*(l4.a1.x-l4.a2.x)-(l4.a1.y-l4.a2.y)*(l1.a1.x-l1.a2.x));
206                         if((xj>=Math.min(l4.a1.x,l4.a2.x)&&xj<=Math.max(l4.a1.x,l4.a2.x))||(yj>=Math.min(l4.a1.y,l4.a2.y)&&yj<=Math.max(l4.a1.y,l4.a2.y)))
207                             if((xj!=x0&&yj!=y0)&&(xj!=xi&&yj!=yi)){
208                             flag = flag+1;
209                             lp3 = 1;
210                         }
211                     }
212                     else if(l4.isParallelOrNot(l1) == 1){
213                         double leng = Math.abs((p5.y-p4.y)*p1.x+(p4.x-p5.x)*p1.y+p5.x*p4.y-p5.y*p4.x)/Math.sqrt((p5.y-p4.y)*(p5.y-p4.y)+(p5.x-p4.x)*(p5.x-p4.x));
214                         if(leng==0){
215                             System.out.print("The point is on the edge of the triangle");
216                             return;
217                         }
218                     }
219                     if(flag < 2)
220                         System.out.print(flag);
221                     else{
222                         if(lp2 == 0)
223                         System.out.print(flag+" "+x0+","+y0+" "+xj+","+yj);
224                         else if(lp3 == 0)
225                             System.out.print(flag+" "+x0+","+y0+" "+xi+","+yi);
226                         else if(lp1 == 0)
227                             System.out.print(flag+" "+xi+","+yi+" "+xj+","+yj);
228                     }
229                 }
230             }
231         //选项5
232         
233         }
234         else{
235             if(n1.length!=4)
236                 System.out.print("wrong number of points");
237             else{
238                 double a = new Double(point[1]);
239                 double b = new Double(point[2]);
240                 double c = new Double(point[3]);
241                 double d = new Double(point[4]);
242                 double e = new Double(point[5]);
243                 double f = new Double(point[6]);
244                 double g = new Double(point[7]);
245                 double h = new Double(point[8]);
246                 Dian p1 = new Dian();
247                 Dian p2 = new Dian();
248                 Dian p3 = new Dian();
249                 Dian p4 = new Dian();
250                 p1.setxy(a,b);
251                 p2.setxy(c,d);
252                 p3.setxy(e,f);
253                 p4.setxy(g,h);
254                 //p5.setxy(p,q);
255                 Xian l1 = new Xian();
256                 Xian l2 = new Xian();
257                 Xian l3 = new Xian();
258                 //Xian l4 = new Xian();
259                 l1.setXY(p2,p3);
260                 l2.setXY(p3,p4);
261                 l3.setXY(p2,p4);
262                 if(p2.pointsCoincide(p3)==0||p2.pointsCoincide(p4)==0||p3.pointsCoincide(p4)==0)//构成直线的两点重合
263                     System.out.print("points coincide");
264                 else {
265                     double a0 = l1.getXianLength();
266                     double b0 = l2.getXianLength();
267                     double c0 = l3.getXianLength();
268                     if(a0+b0<c0&&a0+c0<b0&&b0+c0<a0){
269                         System.out.print("data error");
270                         return;
271                     }
272                     System.out.print("in the triangle");
273                 }
274             }
275         }
276     }
277 }
278 //点
279 class Dian{
280     double x,y;
281     public void setxy(double x,double y){
282         this.x=x;
283         this.y=y;
284     }
285     public double distance(Dian b1){
286         return Math.sqrt((this.x-b1.x)*(this.x-b1.x)+(this.y-b1.y)*(this.y-b1.y));
287     }
288     public int pointsCoincide(Dian b2){//两点是否重合
289         if(this.x==b2.x&&this.y==b2.y)
290             return 0;
291         else 
292             return 1;
293     }
294 }
295 //线
296 class Xian{
297     Dian a1 = new Dian();
298     Dian a2 = new Dian();
299     public void setXY(Dian x1,Dian y1){
300         this.a1=x1;
301         this.a2=y1;
302     }
303     public double getXianLength(){
304         return this.a1.distance(this.a2);
305     }
306     public double Slope(){
307             return (this.a2.y-this.a1.y)/(this.a2.x-this.a1.x);
308     }
309     public int isParallelOrNot(Xian l0){//两条直线是否平行
310       if(this.a1.pointsCoincide(this.a2)==1&&l0.a1.pointsCoincide(l0.a2)==1){//判断线的两点是否重合
311          if(this.a1.x!=this.a2.x&&l0.a1.x!=l0.a2.x){//斜率存在
312              if(this.Slope()==l0.Slope())
313                  return 1;//平行
314              else 
315                  return -1;
316          }
317          else if(this.a1.x==this.a2.x&&l0.a1.x==l0.a2.x)//斜率都不存在
318              return 1;//平行
319      }
320      return 0;
321     }
322     //判断点是否在线段内
323     /*public int inXian(Dian b1){
324         int tag = 0;
325         if((b1.x>Math.min(this.a1.x,this.a2.x)&&b1.x<Math.max(this.a1.x,this.a2.x))||(b1.y>Math.min(this.a1.y,this.a2.y)&&b1.y<Math.max(this.a1.y,this.a2.y)))
326             tag = 1;
327         return tag;
328     }*/
329 }

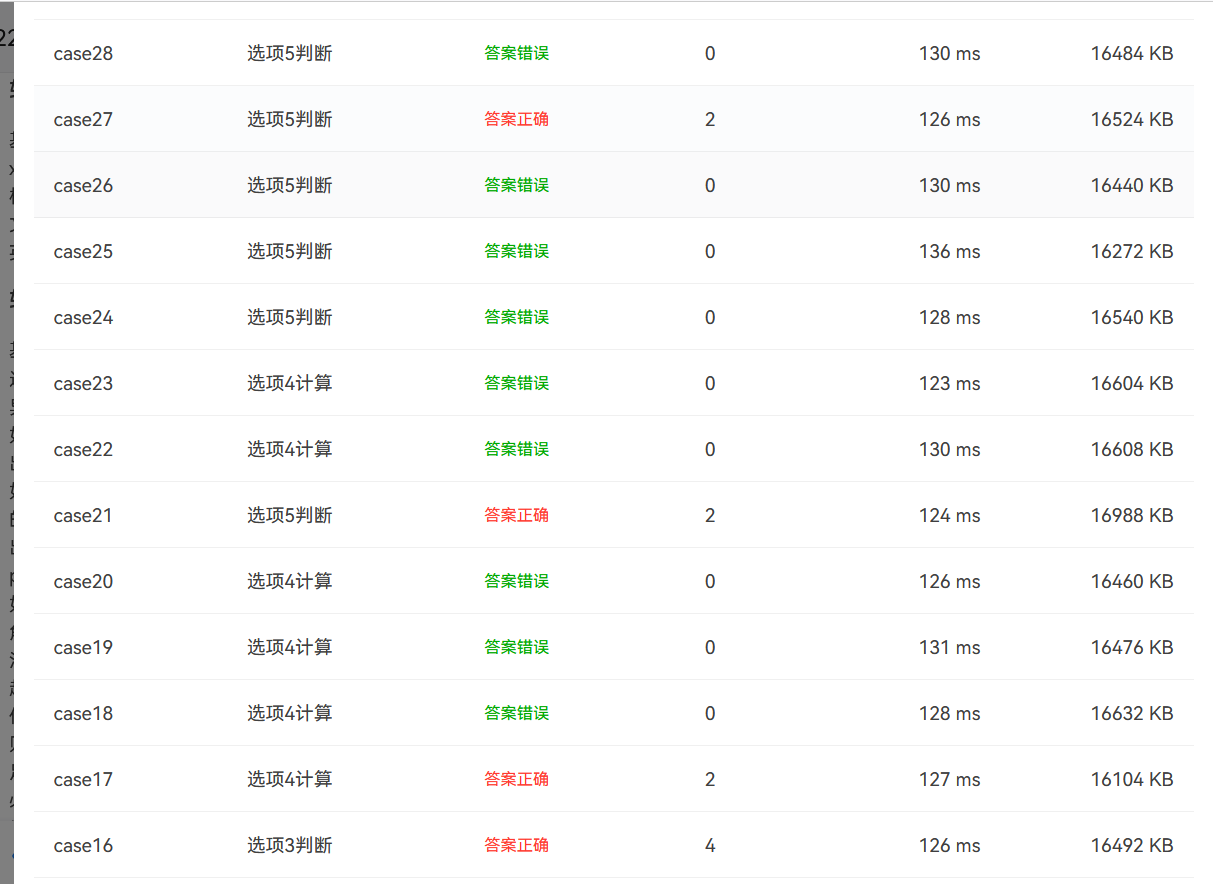
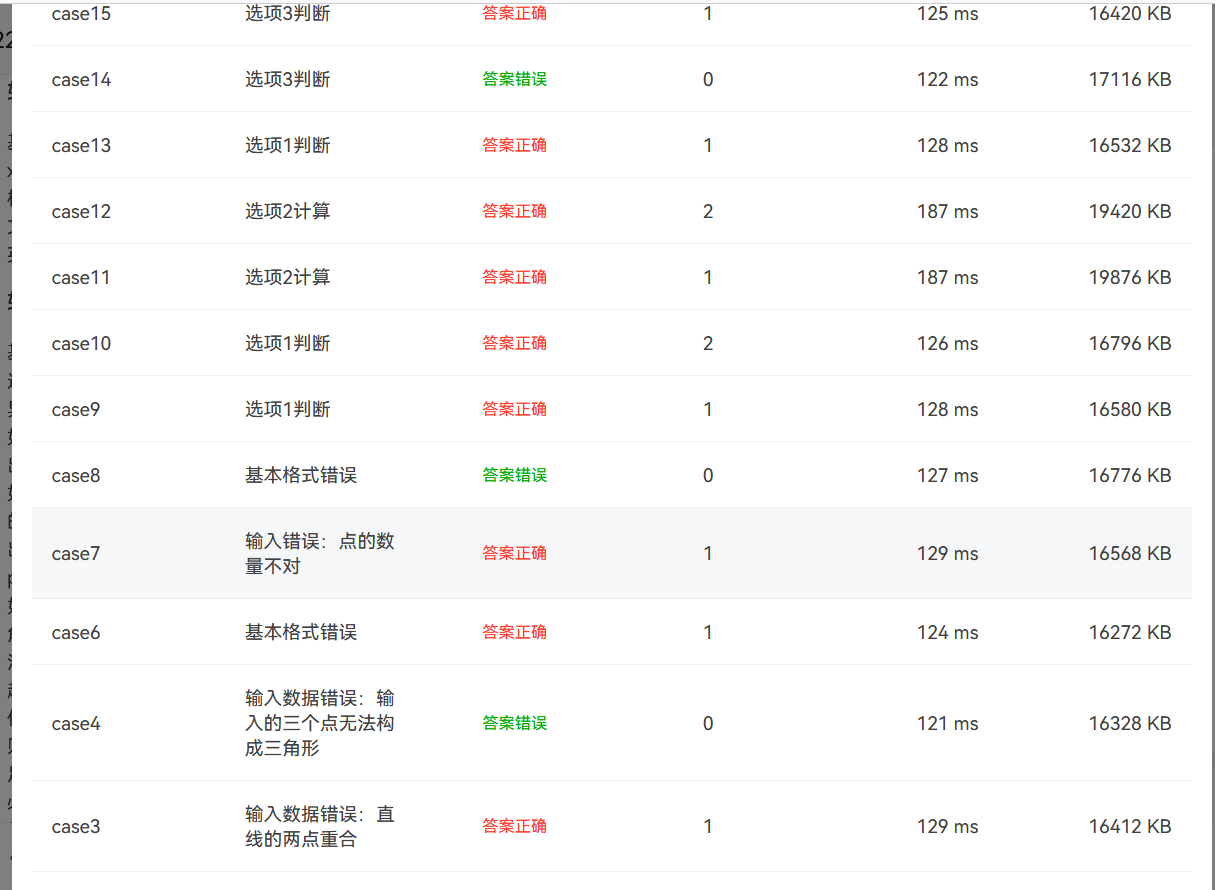
后面两个小题都基本没有得分。

  1 import java.util.Scanner;
  2 public class Main{
  3     public static void main(String args[]){
  4         Scanner input = new Scanner(System.in);
  5         String s = input.nextLine();
  6         //判断输入格式正误
  7         String[] n = s.split("[ ,]");
  8         for(int i=0;i<n.length;i++){
  9             if(i==0&&!n[0].matches("^[1-5]:[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$")){
 10                 System.out.print("Wrong Format");
 11                 return;
 12             }
 13             else if(i>0&&!n[i].matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$")){
 14                 System.out.print("Wrong Format");
 15                 return;
 16             }
 17         }
 18         String[] point = s.split(",| |:");
 19         String[] n1 = s.split(" ");
 20         if(point[0].equals("2")||point[0].equals("1")||point[0].equals("3")){
 21             if(n1.length!=3)
 22                 System.out.print("wrong number of points");
 23             else{
 24                 double a = new Double(point[1]);
 25                 double b = new Double(point[2]);
 26                 double c = new Double(point[3]);
 27                 double d = new Double(point[4]);
 28                 double e = new Double(point[5]);
 29                 double f = new Double(point[6]);
 30                 Dian p1 = new Dian();
 31                 Dian p2 = new Dian();
 32                 Dian p3 = new Dian();
 33                 p1.setxy(a,b);
 34                 p2.setxy(c,d);
 35                 p3.setxy(e,f);
 36                 Xian l1 = new Xian();
 37                 Xian l2 = new Xian();
 38                 Xian l3 = new Xian();
 39                 l1.setXY(p1,p2);
 40                 l2.setXY(p1,p3);
 41                 l3.setXY(p2,p3);
 42                 double ax = l1.getXianLength();
 43                 double bx = l2.getXianLength();
 44                 double cx = l3.getXianLength();
 45                 if(p1.pointsCoincide(p2)==0||p1.pointsCoincide(p3)==0||p2.pointsCoincide(p3)==0)//构成直线的两点重合
 46                     System.out.print("data error");
 47                 else{
 48                   if(ax+bx==cx||ax+cx==bx||bx+cx==ax){//共线
 49                     System.out.print("data error");
 50                       return ;
 51                   }
 52                   else{
 53                   //选项1
 54                    if(point[0].equals("1")){
 55                       //等腰和等边
 56                        if(p1.distance(p2)==p1.distance(p3)||p1.distance(p2)==p2.distance(p3)||p1.distance(p3)==p2.distance(p3)){
 57                             if(p1.distance(p2)==p2.distance(p3)&&p1.distance(p2)==p1.distance(p3))
 58                                 System.out.print("true true");
 59                             else 
 60                                 System.out.print("true false");
 61                        }
 62                        else
 63                            System.out.print("false false");
 64                  }
 65                   //选项2
 66                   else if(point[0].equals("2")){
 67                       double C0 = l1.getXianLength()+l2.getXianLength()+l3.getXianLength();
 68                       double leng1 = Math.abs((p3.y-p2.y)*p1.x+(p2.x-p3.x)*p1.y+p3.x*p2.y-p3.y*p2.x)/Math.sqrt((p3.y-p2.y)*(p3.y-p2.y)+(p3.x-p2.x)*(p3.x-p2.x));
 69                       double area = 0.5*leng1*l3.getXianLength();
 70                       double x0 = (p1.x+p2.x+p3.x)/3;
 71                       double y0 = (p1.y+p2.y+p3.y)/3;
 72                       if((C0*1000000)%10 != 0){
 73                           String CC = String.format("%.6f",C0);
 74                           System.out.print(CC);
 75                       }
 76                       else 
 77                           System.out.print(C0);
 78                       if((area*1000000)%10 != 0){
 79                           String Area = String.format("%.6f",area);
 80                           System.out.print(" "+Area);
 81                       }
 82                       else 
 83                           System.out.print(" "+area);
 84                       if((x0*1000000)%10 != 0){
 85                           String X0 = String.format("%.6f",x0);
 86                           System.out.print(" "+X0+",");
 87                       }
 88                       else 
 89                           System.out.print(" "+x0+",");
 90                       if((y0*1000000)%10 != 0){
 91                           String Y0 = String.format("%.6f",y0);
 92                           System.out.print(Y0);
 93                       }
 94                       else 
 95                           System.out.print(y0);
 96                   }
 97                   //选项3
 98                   else{
 99                       
100                       double a0 = Math.sqrt((p2.x-p3.x)*(p2.x-p3.x)+(p2.y-p3.y)*(p2.y-p3.y));
101                       double b0 = Math.sqrt((p1.x-p3.x)*(p1.x-p3.x)+(p1.y-p3.y)*(p1.y-p3.y));
102                       double c0 = Math.sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
103                       double A = Math.toDegrees(Math.acos((a0*a0-b0*b0-c0*c0)/(-2*b0*c0)));
104                       double B = Math.toDegrees(Math.acos((b0*b0-a0*a0-c0*c0)/(-2*a0*c0)));
105                       double C = Math.toDegrees(Math.acos((c0*c0-b0*b0-a0*a0)/(-2*b0*a0)));
106                       if(A==90||B==90||C==90)
107                           System.out.print("false true false");
108                       else if(A>90||B>90||C>90)
109                           System.out.print("true false false");
110                       else if(A<90&&B<90&&C<90)
111                           System.out.print("false false true");
112                    }
113                   }
114               }
115             }
116         }
117         //选项四
118         else if(point[0].equals("4")){
119             if(n1.length!=5)
120             System.out.print("wrong number of points");
121             else{
122                 double a = new Double(point[1]);
123                 double b = new Double(point[2]);
124                 double c = new Double(point[3]);
125                 double d = new Double(point[4]);
126                 double e = new Double(point[5]);
127                 double f = new Double(point[6]);
128                 double g = new Double(point[7]);
129                 double h = new Double(point[8]);
130                 double p = new Double(point[9]);
131                 double q = new Double(point[10]);
132                 Dian p1 = new Dian();
133                 Dian p2 = new Dian();
134                 Dian p3 = new Dian();
135                 Dian p4 = new Dian();
136                 Dian p5 = new Dian();
137                 p1.setxy(a,b);
138                 p2.setxy(c,d);
139                 p3.setxy(e,f);
140                 p4.setxy(g,h);
141                 p5.setxy(p,q);
142                 Xian l1 = new Xian();
143                 Xian l2 = new Xian();
144                 Xian l3 = new Xian();
145                 Xian l4 = new Xian();
146                 l1.setXY(p1,p2);
147                 l2.setXY(p3,p4);
148                 l3.setXY(p3,p5);
149                 l4.setXY(p4,p5);
150                 double a0 = l2.getXianLength();
151                 double b0 = l3.getXianLength();
152                 double c0 = l4.getXianLength();
153                 if(p1.pointsCoincide(p2)==0||p4.pointsCoincide(p3)==0||p5.pointsCoincide(p4)==0||p3.pointsCoincide(p5)==0)//构成直线的两点重合
154                     System.out.print("points coincide");
155                 else if(l2.Slope()==l3.Slope()||l3.Slope()==l4.Slope()||l2.Slope()==l4.Slope()||(p3.x==p4.x&&p3.x==p5.x))
156                     System.out.print("data error");
157                 else{
158                     int flag = 0;
159                     int lp1=0,lp2 = 0,lp3 = 0;
160                     double x0=0,y0=0;
161                     double xi=0,yi=0;
162                     double xj=0,yj=0;
163                     
164                     if(l2.isParallelOrNot(l1) == -1){
165                         //double x0=0;
166                           // double y0=0;
167                            x0 = ((l2.a1.x-l2.a2.x)*(l1.a1.y*l1.a2.x-l1.a1.x*l1.a2.y)-(l1.a1.x-l1.a2.x)*(l2.a1.y*l2.a2.x-l2.a1.x*l2.a2.y))/((l1.a1.y-l1.a2.y)*(l2.a1.x-l2.a2.x)-(l2.a1.y-l2.a2.y)*(l1.a1.x-l1.a2.x));
168                            y0 = ((l2.a1.y-l2.a2.y)*(l1.a1.y*l1.a2.x-l1.a1.x*l1.a2.y)-(l1.a1.y-l1.a2.y)*(l2.a1.y*l2.a2.x-l2.a1.x*l2.a2.y))/((l1.a1.y-l1.a2.y)*(l2.a1.x-l2.a2.x)-(l2.a1.y-l2.a2.y)*(l1.a1.x-l1.a2.x));
169                         
170                         if((x0>=Math.min(l2.a1.x,l2.a2.x)&&x0<=Math.max(l2.a1.x,l2.a2.x))||(y0>=Math.min(l2.a1.y,l2.a2.y)&&y0<=Math.max(l2.a1.y,l2.a2.y))){
171                             flag = flag+1;
172                             lp1 = 1;
173                         }
174                     }
175                     else if(l2.isParallelOrNot(l1) == 1){
176                         double leng = Math.abs((p4.y-p3.y)*p1.x+(p3.x-p4.x)*p1.y+p4.x*p3.y-p4.y*p3.x)/Math.sqrt((p4.y-p3.y)*(p4.y-p3.y)+(p4.x-p3.x)*(p4.x-p3.x));
177                         if(leng==0){
178                             System.out.print("The point is on the edge of the triangle");
179                             return;
180                         }
181                     }
182                     if(l3.isParallelOrNot(l1) == -1){
183                         //double xi=0;
184                         //double yi=0;
185                         xi = ((l3.a1.x-l3.a2.x)*(l1.a1.y*l1.a2.x-l1.a1.x*l1.a2.y)-(l1.a1.x-l1.a2.x)*(l3.a1.y*l3.a2.x-l3.a1.x*l3.a2.y))/((l1.a1.y-l1.a2.y)*(l3.a1.x-l3.a2.x)-(l3.a1.y-l3.a2.y)*(l1.a1.x-l1.a2.x));
186                         yi = ((l3.a1.y-l3.a2.y)*(l1.a1.y*l1.a2.x-l1.a1.x*l1.a2.y)-(l1.a1.y-l1.a2.y)*(l3.a1.y*l3.a2.x-l3.a1.x*l3.a2.y))/((l1.a1.y-l1.a2.y)*(l3.a1.x-l3.a2.x)-(l3.a1.y-l3.a2.y)*(l1.a1.x-l1.a2.x));
187                         
188                         if((xi>=Math.min(l3.a1.x,l3.a2.x)&&xi<=Math.max(l3.a1.x,l3.a2.x))||(yi>=Math.min(l3.a1.y,l3.a2.y)&&yi<=Math.max(l3.a1.y,l3.a2.y)))
189                             if(xi!=x0&&yi!=y0){
190                             lp2 = 1;
191                             flag = flag+1;
192                         }
193                     }
194                     else if(l3.isParallelOrNot(l1) == 1){
195                         double leng = Math.abs((p5.y-p3.y)*p1.x+(p3.x-p5.x)*p1.y+p5.x*p3.y-p5.y*p3.x)/Math.sqrt((p5.y-p3.y)*(p5.y-p3.y)+(p5.x-p3.x)*(p5.x-p3.x));
196                         if(leng==0){
197                             System.out.print("The point is on the edge of the triangle");
198                             return;
199                         }
200                     }
201                     if(l4.isParallelOrNot(l1) == -1){
202                         //double xj=0;
203                         //double yj=0;
204                         xj = ((l4.a1.x-l4.a2.x)*(l1.a1.y*l1.a2.x-l1.a1.x*l1.a2.y)-(l1.a1.x-l1.a2.x)*(l4.a1.y*l4.a2.x-l4.a1.x*l4.a2.y))/((l1.a1.y-l1.a2.y)*(l4.a1.x-l4.a2.x)-(l4.a1.y-l4.a2.y)*(l1.a1.x-l1.a2.x));
205                         yj = ((l4.a1.y-l4.a2.y)*(l1.a1.y*l1.a2.x-l1.a1.x*l1.a2.y)-(l1.a1.y-l1.a2.y)*(l4.a1.y*l4.a2.x-l4.a1.x*l4.a2.y))/((l1.a1.y-l1.a2.y)*(l4.a1.x-l4.a2.x)-(l4.a1.y-l4.a2.y)*(l1.a1.x-l1.a2.x));
206                         if((xj>=Math.min(l4.a1.x,l4.a2.x)&&xj<=Math.max(l4.a1.x,l4.a2.x))||(yj>=Math.min(l4.a1.y,l4.a2.y)&&yj<=Math.max(l4.a1.y,l4.a2.y)))
207                             if((xj!=x0&&yj!=y0)&&(xj!=xi&&yj!=yi)){
208                             flag = flag+1;
209                             lp3 = 1;
210                         }
211                     }
212                     else if(l4.isParallelOrNot(l1) == 1){
213                         double leng = Math.abs((p5.y-p4.y)*p1.x+(p4.x-p5.x)*p1.y+p5.x*p4.y-p5.y*p4.x)/Math.sqrt((p5.y-p4.y)*(p5.y-p4.y)+(p5.x-p4.x)*(p5.x-p4.x));
214                         if(leng==0){
215                             System.out.print("The point is on the edge of the triangle");
216                             return;
217                         }
218                     }
219                     if(flag < 2)
220                         System.out.print(flag);
221                     else{
222                         if(lp2 == 0)
223                         System.out.print(flag+" "+x0+","+y0+" "+xj+","+yj);
224                         else if(lp3 == 0)
225                             System.out.print(flag+" "+x0+","+y0+" "+xi+","+yi);
226                         else if(lp1 == 0)
227                             System.out.print(flag+" "+xi+","+yi+" "+xj+","+yj);
228                     }
229                 }
230             }
231         //选项5
232         
233         }
234         else{
235             if(n1.length!=4)
236                 System.out.print("wrong number of points");
237             else{
238                 double a = new Double(point[1]);
239                 double b = new Double(point[2]);
240                 double c = new Double(point[3]);
241                 double d = new Double(point[4]);
242                 double e = new Double(point[5]);
243                 double f = new Double(point[6]);
244                 double g = new Double(point[7]);
245                 double h = new Double(point[8]);
246                 Dian p1 = new Dian();
247                 Dian p2 = new Dian();
248                 Dian p3 = new Dian();
249                 Dian p4 = new Dian();
250                 p1.setxy(a,b);
251                 p2.setxy(c,d);
252                 p3.setxy(e,f);
253                 p4.setxy(g,h);
254                 //p5.setxy(p,q);
255                 Xian l1 = new Xian();
256                 Xian l2 = new Xian();
257                 Xian l3 = new Xian();
258                 //Xian l4 = new Xian();
259                 l1.setXY(p2,p3);
260                 l2.setXY(p3,p4);
261                 l3.setXY(p2,p4);
262                 if(p2.pointsCoincide(p3)==0||p2.pointsCoincide(p4)==0||p3.pointsCoincide(p4)==0)//构成直线的两点重合
263                     System.out.print("points coincide");
264                 else {
265                     double a0 = l1.getXianLength();
266                     double b0 = l2.getXianLength();
267                     double c0 = l3.getXianLength();
268                     if(a0+b0<c0&&a0+c0<b0&&b0+c0<a0){
269                         System.out.print("data error");
270                         return;
271                     }
272                     System.out.print("in the triangle");
273                 }
274             }
275         }
276     }
277 }
278 //点
279 class Dian{
280     double x,y;
281     public void setxy(double x,double y){
282         this.x=x;
283         this.y=y;
284     }
285     public double distance(Dian b1){
286         return Math.sqrt((this.x-b1.x)*(this.x-b1.x)+(this.y-b1.y)*(this.y-b1.y));
287     }
288     public int pointsCoincide(Dian b2){//两点是否重合
289         if(this.x==b2.x&&this.y==b2.y)
290             return 0;
291         else 
292             return 1;
293     }
294 }
295 //线
296 class Xian{
297     Dian a1 = new Dian();
298     Dian a2 = new Dian();
299     public void setXY(Dian x1,Dian y1){
300         this.a1=x1;
301         this.a2=y1;
302     }
303     public double getXianLength(){
304         return this.a1.distance(this.a2);
305     }
306     public double Slope(){
307             return (this.a2.y-this.a1.y)/(this.a2.x-this.a1.x);
308     }
309     public int isParallelOrNot(Xian l0){//两条直线是否平行
310       if(this.a1.pointsCoincide(this.a2)==1&&l0.a1.pointsCoincide(l0.a2)==1){//判断线的两点是否重合
311          if(this.a1.x!=this.a2.x&&l0.a1.x!=l0.a2.x){//斜率存在
312              if(this.Slope()==l0.Slope())
313                  return 1;//平行
314              else 
315                  return -1;
316          }
317          else if(this.a1.x==this.a2.x&&l0.a1.x==l0.a2.x)//斜率都不存在
318              return 1;//平行
319      }
320      return 0;
321     }
322     //判断点是否在线段内
323     /*public int inXian(Dian b1){
324         int tag = 0;
325         if((b1.x>Math.min(this.a1.x,this.a2.x)&&b1.x<Math.max(this.a1.x,this.a2.x))||(b1.y>Math.min(this.a1.y,this.a2.y)&&b1.y<Math.max(this.a1.y,this.a2.y)))
326             tag = 1;
327         return tag;
328     }*/
329 }View Code

三、踩坑心得

第一次作业：

（1）if判断条件中‘==’号写错。成‘=’

（2）三角形成立的判断条件写a+b>c（两边之和大于第三边）过不了，后面改成a+b-c=0.00001才过。

第二次作业：

（1）字符串类型与其他数字类型的转换，遇到好多次了。

（2）取出字符串中的子字符与其他数值相比需要用字符串函数，不能直接‘=’，而是用equal函数。

（3）对输入格式的判断，需要用正则表达式，刚开始不知道这个，经常写很长的表达式容易出错。

（4）第二题需要用到奇偶校验。感觉测试有问题，我写的判断条件相反才正确，否则就错误。

第三次作业：

（1）数值类型的转换，前面是double后面可能就是float。

（2）输入格式有些测试点过不了，不知道是那个点给遗漏了。

（3）然后其他的坑的话就不好说了，第2,3题好多测试点没过，算法不会，很考验数学吧。

总的来说，在写代码时需要有非常严谨的思想，要细心。同时其他方面的知识也要多去了解并掌握，才能写出更好的代码。

四、改进建议

前两次作业中我都只是运用了一个类来写，并没有使用JAVA面向对象的思想来设计，且代码的注释写的不是很清楚。虽然题目比较简单，代码比较容易看懂，但还是建议用JAVA面向对象的思想写比较方便其他人看懂，方便修改维护。第三次作业其实是一个很大的题目，只是分为了三个部分。虽然我用了点，线类来写，但题目要求我们写的功能很多，我并没有分多个类，多个方法，所以看最后赠个代码的圈复杂度还是很高。建议自己多看一些JAVA面向对象思想的书或者视频，加深对这种思想的认识，多使用类，方法，最好不要一个类代码超过50行。然后适应一下类的注释方法。例如：

 1 /*
 2 *点的描述，包括设置点的坐标，求两点之间的距离，判断两点是否重合
 3 *方法名：setxy,distance,pointsCoincide
 4 *属性：x,y
 5 */
 6 class Dian{
 7     double x,y;
 8     public void setxy(double x,double y){
 9         this.x=x;
10         this.y=y;
11     }
12     public double distance(Dian b1){
13         return Math.sqrt((this.x-b1.x)*(this.x-b1.x)+(this.y-b1.y)*(this.y-b1.y));
14     }
15     public int pointsCoincide(Dian b2){//两点是否重合
16         if(this.x==b2.x&&this.y==b2.y)
17             return 0;
18         else 
19             return 1;
20     }
21 }

1     /*
2      *求两点之间的距离
3      *参数：点 b1
4      *返回值类型：Double
5     */
6     public double distance(Dian b1){
7         return Math.sqrt((this.x-b1.x)*(this.x-b1.x)+(this.y-b1.y)*(this.y-b1.y));
8     }

五、总结

通过前三次大作业，首先我学会了如何在PTA中使用Main类来写代码，然后熟悉了使用Scanner类来输入的方法，以及System类不同输出方法的差别和使用方法。熟练了对字符串进行操作的方法的使用。同时遇到数值时需要考虑数值类型的转换。还有遇到输入格式判断时，可以使用正则表达式，可以大大减少代码字数。这些基本的JAVA知识也是与C语言不同的地方。当然最大的不同是，JAVA是面向对象的，而C语言是面向过程的。在使用代码时JAVA可以一个代码到处运行，非常方便，且如果规范编写JAVA代码将会很利于同行的使用，以及测试人员的检查维护。虽然我知道JAVA的方便之处，但前三次作业中我并没有感受到很大的便利，我对JAVA类的设计还不太会使用，还有这些作业中我发现自己对很多题目的算法并不太会，有的写出来后没有得到分，数学方面的知识不太过关，这是我今后需要改进的。然后我觉得JAVA课的作业时间太紧凑了，且后面的题目需要前面的基垫，对于一些基础不太好的同学来说似乎过于困难了，例如我吧。。。然后题目的测试点希望可以给的详细一些，多给点提示。

posted @ 2022-10-02 22:39 我也不想这样阅读(73) 评论(0) 收藏举报

刷新页面返回顶部

java-036

1-3次作业总结

公告