使用sklearn进行集成学习——实践

系列

• 《使用sklearn进行集成学习——理论》
• 《使用sklearn进行集成学习——实践》

目录

1 Random Forest和Gradient Tree Boosting参数详解
2 如何调参？
　　2.1 调参的目标：偏差和方差的协调
　　2.2 参数对整体模型性能的影响
　　2.3 一个朴实的方案：贪心的坐标下降法
　　　　2.3.1 Random Forest调参案例：Digit Recognizer
　　　　　　2.3.1.1 调整过程影响类参数
　　　　　　2.3.1.2 调整子模型影响类参数
　　　　2.3.2 Gradient Tree Boosting调参案例：Hackathon3.x
　　　　　　2.3.2.1 调整过程影响类参数
　　　　　　2.3.2.2 调整子模型影响类参数
　　　　　　2.3.2.3 杀一记回马枪
　　2.4 “局部最优解”（温馨提示：看到这里有彩蛋！）
　　2.5 类别不均衡的陷阱
3 总结
4 参考资料

---

1 Random Forest和Gradient Tree Boosting参数详解

　　在sklearn.ensemble库中，我们可以找到Random Forest分类和回归的实现：RandomForestClassifier和RandomForestRegression，Gradient Tree Boosting分类和回归的实现：GradientBoostingClassifier和GradientBoostingRegression。有了这些模型后，立马上手操练起来？少侠请留步！且听我说一说，使用这些模型时常遇到的问题：

• 明明模型调教得很好了，可是效果离我的想象总有些偏差？——模型训练的第一步就是要定好目标，往错误的方向走太多也是后退。
• 凭直觉调了某个参数，可是居然没有任何作用，有时甚至起到反作用？——定好目标后，接下来就是要确定哪些参数是影响目标的，其对目标是正影响还是负影响，影响的大小。
• 感觉训练结束遥遥无期，sklearn只是个在小数据上的玩具？——虽然sklearn并不是基于分布式计算环境而设计的，但我们还是可以通过某些策略提高训练的效率。
• 模型开始训练了，但是训练到哪一步了呢？——饱暖思淫欲啊，目标，性能和效率都得了满足后，我们有时还需要有别的追求，例如训练过程的输出，袋外得分计算等等。

　　通过总结这些常见的问题，我们可以把模型的参数分为4类：目标类、性能类、效率类和附加类。下表详细地展示了4个模型参数的意义：

参数	类型	RandomForestClassifier	RandomForestRegressor	GradientBoostingClassifier	GradientBoostingRegressor
loss	目标			损失函数 ● exponential：模型等同AdaBoost ★ deviance：和Logistic Regression的损失函数一致	损失函数 ● exponential：模型等同AdaBoost ★ deviance：和Logistic Regression的损失函数一致
alpha	目标			损失函数为huber或quantile的时，alpha为损失函数中的参数	损失函数为huber或quantile的时，alpha为损失函数中的参数
class_weight	目标	类别的权值
n_estimators	性能	子模型的数量 ● int：个数 ★ 10：默认值	子模型的数量 ● int：个数 ★ 10：默认值	子模型的数量 ● int：个数 ★ 100：默认值	子模型的数量 ● int：个数 ★ 100：默认值
learning_rate	性能			学习率（缩减）	学习率（缩减）
criterion	性能	判断节点是否继续分裂采用的计算方法 ● entropy ★ gini	判断节点是否继续分裂采用的计算方法 ★ mse
max_features	性能	节点分裂时参与判断的最大特征数 ● int：个数 ● float：占所有特征的百分比 ★ auto：所有特征数的开方 ● sqrt：所有特征数的开方 ● log2：所有特征数的log2值 ● None：等于所有特征数	节点分裂时参与判断的最大特征数 ● int：个数 ● float：占所有特征的百分比 ★ auto：所有特征数的开方 ● sqrt：所有特征数的开方 ● log2：所有特征数的log2值 ● None：等于所有特征数	节点分裂时参与判断的最大特征数 ● int：个数 ● float：占所有特征的百分比 ● auto：所有特征数的开方 ● sqrt：所有特征数的开方 ● log2：所有特征数的log2值 ★ None：等于所有特征数	节点分裂时参与判断的最大特征数 ● int：个数 ● float：占所有特征的百分比 ● auto：所有特征数的开方 ● sqrt：所有特征数的开方 ● log2：所有特征数的log2值 ★ None：等于所有特征数
max_depth	性能	最大深度，如果max_leaf_nodes参数指定，则忽略 ● int：深度 ★ None：树会生长到所有叶子都分到一个类，或者某节点所代表的样本数已小于min_samples_split	最大深度，如果max_leaf_nodes参数指定，则忽略 ● int：深度 ★ None：树会生长到所有叶子都分到一个类，或者某节点所代表的样本数已小于min_samples_split	最大深度，如果max_leaf_nodes参数指定，则忽略 ● int：深度 ★ 3：默认值	最大深度，如果max_leaf_nodes参数指定，则忽略 ● int：深度 ★ 3：默认值
min_samples_split	性能	分裂所需的最小样本数 ● int：样本数 ★ 2：默认值	分裂所需的最小样本数 ● int：样本数 ★ 2：默认值	分裂所需的最小样本数 ● int：样本数 ★ 2：默认值	分裂所需的最小样本数 ● int：样本数 ★ 2：默认值
min_samples_leaf	性能	叶节点最小样本数 ● int：样本数 ★ 1：默认值	叶节点最小样本数 ● int：样本数 ★ 1：默认值	叶节点最小样本数 ● int：样本数 ★ 1：默认值	叶节点最小样本数 ● int：样本数 ★ 1：默认值
min_weight_fraction_leaf	性能	叶节点最小样本权重总值 ● float：权重总值 ★ 0：默认值	叶节点最小样本权重总值 ● float：权重总值 ★ 0：默认值	叶节点最小样本权重总值 ● float：权重总值 ★ 0：默认值	叶节点最小样本权重总值 ● float：权重总值 ★ 0：默认值
max_leaf_nodes	性能	最大叶节点数 ● int：个数 ★ None：不限制叶节点数	最大叶节点数 ● int：个数 ★ None：不限制叶节点数	最大叶节点数 ● int：个数 ★ None：不限制叶节点数	最大叶节点数 ● int：个数 ★ None：不限制叶节点数
bootstrap	性能	是否bootstrap对样本抽样 ● False：子模型的样本一致，子模型间强相关 ★ True：默认值	是否bootstrap对样本抽样 ● False：子模型的样本一致，子模型间强相关 ★ True：默认值
subsample	性能			子采样率 ● float：采样率 ★ 1.0：默认值	子采样率 ● float：采样率 ★ 1.0：默认值
init	性能			初始子模型	初始子模型
n_jobs	效率	并行数 ● int：个数 ● -1：跟CPU核数一致 ★ 1:默认值	并行数 ● int：个数 ● -1：跟CPU核数一致 ★ 1:默认值
warm_start	效率	是否热启动，如果是，则下一次训练是以追加树的形式进行 ● bool：热启动 ★ False：默认值	是否热启动，如果是，则下一次训练是以追加树的形式进行 ● bool：热启动 ★ False：默认值	是否热启动，如果是，则下一次训练是以追加树的形式进行 ● bool：热启动 ★ False：默认值	是否热启动，如果是，则下一次训练是以追加树的形式进行 ● bool：热启动 ★ False：默认值
presort	效率			是否预排序,预排序可以加速查找最佳分裂点，对于稀疏数据不管用 ● Bool ★ auto：非稀疏数据则预排序，若稀疏数据则不预排序	是否预排序,预排序可以加速查找最佳分裂点，对于稀疏数据不管用 ● Bool ★ auto：非稀疏数据则预排序，若稀疏数据则不预排序
oob_score	附加	是否计算袋外得分 ★ False：默认值	是否计算袋外得分 ★ False：默认值
random_state	附加	随机器对象	随机器对象	随机器对象	随机器对象
verbose	附加	日志冗长度 ● int：冗长度 ★ 0：不输出训练过程 ● 1：偶尔输出 ● >1：对每个子模型都输出	日志冗长度 ● int：冗长度 ★ 0：不输出训练过程 ● 1：偶尔输出 ● >1：对每个子模型都输出	日志冗长度 ● int：冗长度 ★ 0：不输出训练过程 ● 1：偶尔输出 ● >1：对每个子模型都输出	日志冗长度 ● int：冗长度 ★ 0：不输出训练过程 ● 1：偶尔输出 ● >1：对每个子模型都输出

# ★：默认值

　　不难发现，基于bagging的Random Forest模型和基于boosting的Gradient Tree Boosting模型有不少共同的参数，然而某些参数的默认值又相差甚远。在《使用sklearn进行集成学习——理论》一文中，我们对bagging和boosting两种集成学习技术有了初步的了解。Random Forest的子模型都拥有较低的偏差，整体模型的训练过程旨在降低方差，故其需要较少的子模型（n_estimators默认值为10）且子模型不为弱模型（max_depth的默认值为None），同时，降低子模型间的相关度可以起到减少整体模型的方差的效果（max_features的默认值为auto）。另一方面，Gradient Tree Boosting的子模型都拥有较低的方差，整体模型的训练过程旨在降低偏差，故其需要较多的子模型（n_estimators默认值为100）且子模型为弱模型（max_depth的默认值为3），但是降低子模型间的相关度不能显著减少整体模型的方差（max_features的默认值为None）。

---

 

2 如何调参？

　　聪明的读者应当要发问了：”博主，就算你列出来每个参数的意义，然并卵啊！我还是不知道无从下手啊！”

　　参数分类的目的在于缩小调参的范围，首先我们要明确训练的目标，把目标类的参数定下来。接下来，我们需要根据数据集的大小，考虑是否采用一些提高训练效率的策略，否则一次训练就三天三夜，法国人孩子都生出来了。然后，我们终于进入到了重中之重的环节：调整那些影响整体模型性能的参数。

2.1 调参的目标：偏差和方差的协调

　　同样在《使用sklearn进行集成学习——理论》中，我们已讨论过偏差和方差是怎样影响着模型的性能——准确度。调参的目标就是为了达到整体模型的偏差和方差的大和谐！进一步，这些参数又可分为两类：过程影响类及子模型影响类。在子模型不变的前提下，某些参数可以通过改变训练的过程，从而影响模型的性能，诸如：“子模型数”（n_estimators）、“学习率”（learning_rate）等。另外，我们还可以通过改变子模型性能来影响整体模型的性能，诸如：“最大树深度”（max_depth）、“分裂条件”（criterion）等。正由于bagging的训练过程旨在降低方差，而boosting的训练过程旨在降低偏差，过程影响类的参数能够引起整体模型性能的大幅度变化。一般来说，在此前提下，我们继续微调子模型影响类的参数，从而进一步提高模型的性能。

2.2 参数对整体模型性能的影响

　　假设模型是一个多元函数F，其输出值为模型的准确度。我们可以固定其他参数，从而对某个参数对整体模型性能的影响进行分析：是正影响还是负影响，影响的单调性？

　　对Random Forest来说，增加“子模型数”（n_estimators）可以明显降低整体模型的方差，且不会对子模型的偏差和方差有任何影响。模型的准确度会随着“子模型数”的增加而提高。由于减少的是整体模型方差公式的第二项，故准确度的提高有一个上限。在不同的场景下，“分裂条件”（criterion）对模型的准确度的影响也不一样，该参数需要在实际运用时灵活调整。调整“最大叶节点数”（max_leaf_nodes）以及“最大树深度”（max_depth）之一，可以粗粒度地调整树的结构：叶节点越多或者树越深，意味着子模型的偏差越低，方差越高；同时，调整“分裂所需最小样本数”（min_samples_split）、“叶节点最小样本数”（min_samples_leaf）及“叶节点最小权重总值”（min_weight_fraction_leaf），可以更细粒度地调整树的结构：分裂所需样本数越少或者叶节点所需样本越少，也意味着子模型越复杂。一般来说，我们总采用bootstrap对样本进行子采样来降低子模型之间的关联度，从而降低整体模型的方差。适当地减少“分裂时考虑的最大特征数”（max_features），给子模型注入了另外的随机性，同样也达到了降低子模型之间关联度的效果。但是一味地降低该参数也是不行的，因为分裂时可选特征变少，模型的偏差会越来越大。在下图中，我们可以看到这些参数对Random Forest整体模型性能的影响：

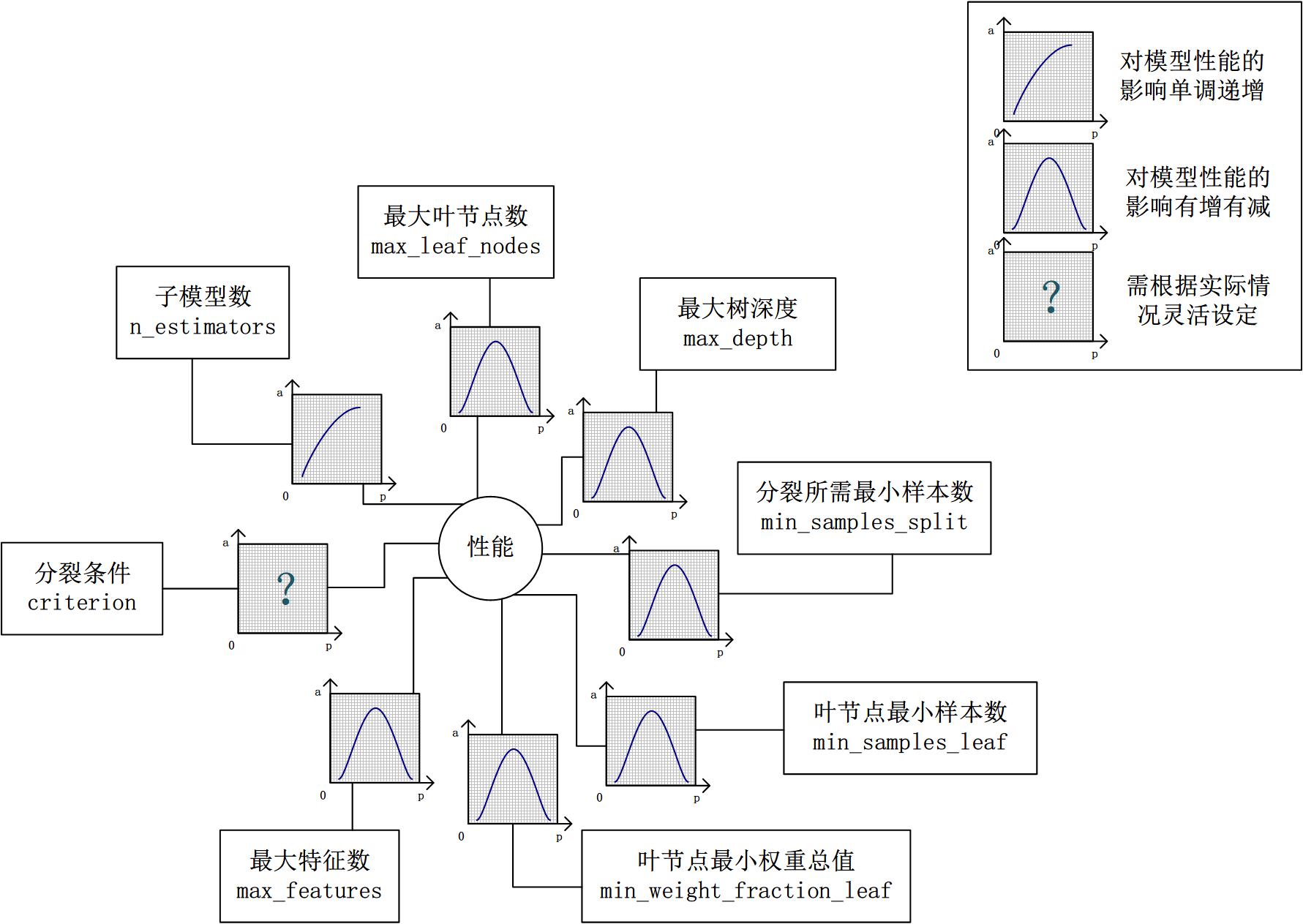
　　对Gradient Tree Boosting来说，“子模型数”（n_estimators）和“学习率”（learning_rate）需要联合调整才能尽可能地提高模型的准确度：想象一下，A方案是走4步，每步走3米，B方案是走5步，每步走2米，哪个方案可以更接近10米远的终点？同理，子模型越复杂，对应整体模型偏差低，方差高，故“最大叶节点数”（max_leaf_nodes）、“最大树深度”（max_depth）等控制子模型结构的参数是与Random Forest一致的。类似“分裂时考虑的最大特征数”（max_features），降低“子采样率”（subsample），也会造成子模型间的关联度降低，整体模型的方差减小，但是当子采样率低到一定程度时，子模型的偏差增大，将引起整体模型的准确度降低。还记得“初始模型”（init）是什么吗？不同的损失函数有不一样的初始模型定义，通常，初始模型是一个更加弱的模型（以“平均”情况来预测），虽说支持自定义，大多数情况下保持默认即可。在下图中，我们可以看到这些参数对Gradient Tree Boosting整体模型性能的影响：

2.3 一个朴实的方案：贪心的坐标下降法

　　到此为止，我们终于知道需要调整哪些参数，对于单个参数，我们也知道怎么调整才能提升性能。然而，表示模型的函数F并不是一元函数，这些参数需要共同调整才能得到全局最优解。也就是说，把这些参数丢给调参算法（诸如Grid Search）咯？对于小数据集，我们还能这么任性，但是参数组合爆炸，在大数据集上，或许我的子子孙孙能够看到训练结果吧。实际上网格搜索也不一定能得到全局最优解，而另一些研究者从解优化问题的角度尝试解决调参问题。

　　坐标下降法是一类优化算法，其最大的优势在于不用计算待优化的目标函数的梯度。我们最容易想到一种特别朴实的类似于坐标下降法的方法，与坐标下降法不同的是，其不是循环使用各个参数进行调整，而是贪心地选取了对整体模型性能影响最大的参数。参数对整体模型性能的影响力是动态变化的，故每一轮坐标选取的过程中，这种方法在对每个坐标的下降方向进行一次直线搜索（line search）。首先，找到那些能够提升整体模型性能的参数，其次确保提升是单调或近似单调的。这意味着，我们筛选出来的参数是对整体模型性能有正影响的，且这种影响不是偶然性的，要知道，训练过程的随机性也会导致整体模型性能的细微区别，而这种区别是不具有单调性的。最后，在这些筛选出来的参数中，选取影响最大的参数进行调整即可。

　　无法对整体模型性能进行量化，也就谈不上去比较参数影响整体模型性能的程度。是的，我们还没有一个准确的方法来量化整体模型性能，只能通过交叉验证来近似计算整体模型性能。然而交叉验证也存在随机性，假设我们以验证集上的平均准确度作为整体模型的准确度，我们还得关心在各个验证集上准确度的变异系数，如果变异系数过大，则平均值作为整体模型的准确度也是不合适的。在接下来的案例分析中，我们所谈及的整体模型性能均是指平均准确度，请各位留心。

2.3.1 Random Forest调参案例：Digit Recognizer

　　在这里，我们选取Kaggle上101教学赛中的Digit Recognizer作为案例来演示对RandomForestClassifier调参的过程。当然，我们也不要傻乎乎地手工去设定不同的参数，然后训练模型。借助sklearn.grid_search库中的GridSearchCV类，不仅可以自动化调参，同时还可以对每一种参数组合进行交叉验证计算平均准确度。

2.3.1.1 调整过程影响类参数

　　首先，我们需要对过程影响类参数进行调整，而Random Forest的过程影响类参数只有“子模型数”（n_estimators）。“子模型数”的默认值为10，在此基础上，我们以10为单位，考察取值范围在1至201的调参情况：

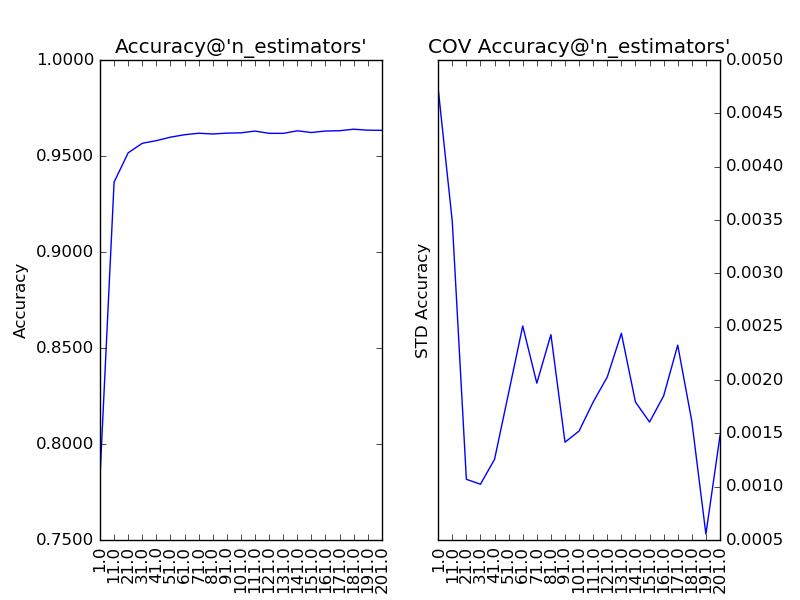
# 左图为模型在验证集上的平均准确度，右图为准确度的变异系数。横轴为参数的取值。

　　通过上图我们可以看到，随着“子模型数”的增加，整体模型的方差减少，其防止过拟合的能力增强，故整体模型的准确度提高。当“子模型数”增加到40以上时，准确度的提升逐渐不明显。考虑到训练的效率，最终我们选择“子模型数”为200。此时，在Kaggle上提交结果，得分为：0.96500，很凑合。

2.3.1.2 调整子模型影响类参数

　　在设定“子模型数”（n_estimators）为200的前提下，我们依次对子模型影响类的参数对整体模型性能的影响力进行分析。

　　对“分裂条件”（criterion）分别取值gini和entropy，得到调参结果如下：

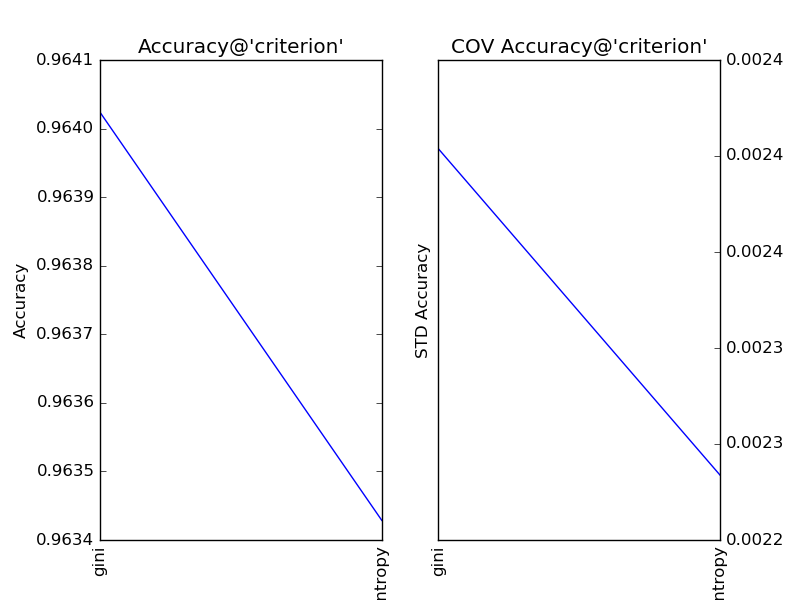
　　显见，在此问题中，“分裂条件”保持默认值gini更加合适。

　　对“分裂时参与判断的最大特征数”（max_feature）以1为单位，设定取值范围为28至47，得到调参结果如下：

　　

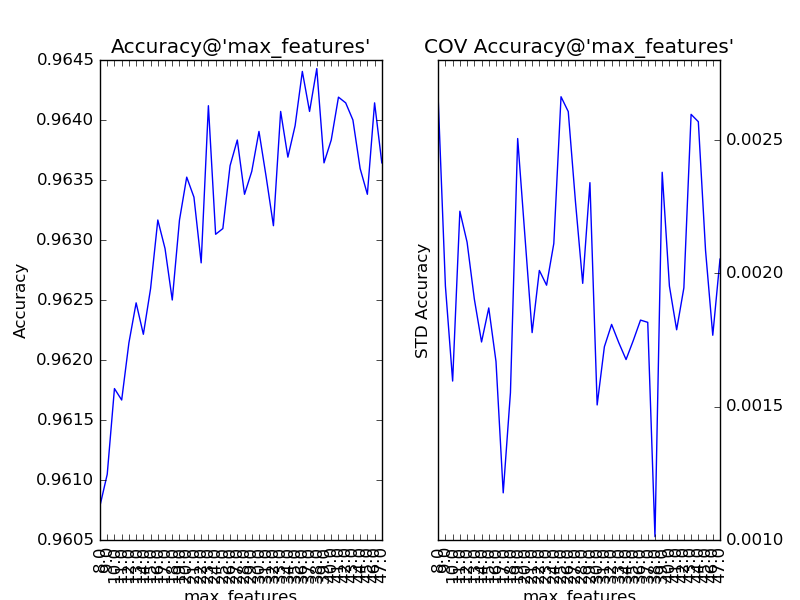
　　“分裂时参与判断的最大特征数”的默认值auto，即总特征数（sqrt(784)=28）的开方。通过提升该参数，整体模型的准确度得到了提升。可见，该参数的默认值过小，导致了子模型的偏差过大，从而整体模型的偏差过大。同时，我们还注意到，该参数对整体模型性能的影响是近似单调的：从28到38，模型的准确度逐步抖动提升。所以，我们可考虑将该参数纳入下一步的调参工作。

　　对“最大深度”（max_depth）以10为单位，设定取值范围为10到100，得到调参结果如下：

　　随着树的深度加深，子模型的偏差减少，整体模型的准确度得到提升。从理论上来说，子模型训练的后期，随着方差增大，子模型的准确度稍微降低，从而影响整体模型的准确度降低。看图中，似乎取值范围从40到60的情况可以印证这一观点。不妨以1为单位，设定取值范围为40到59，更加细致地分析：

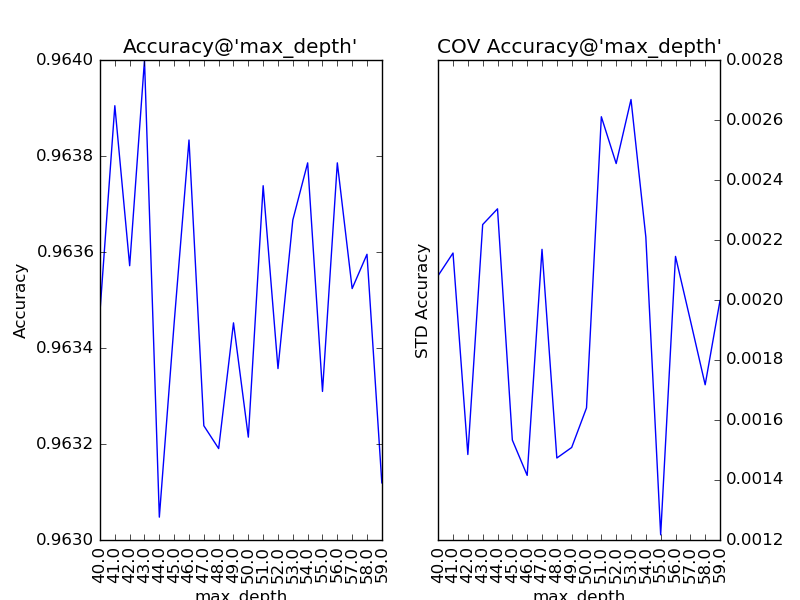
　　有点傻眼了，怎么跟预想的不太一样？为什么模型准确度的变化在40到59之间没有鲜明的“规律”了？要分析这个问题，我们得先思考一下，少一层子节点对子模型意味着什么？若少的那一层给原子模型带来的是方差增大，则新子模型会准确度提高；若少的那一层给原子模型带来的是偏差减小，则新子模型会准确度降低。所以，细粒度的层次变化既可能使整体模型的准确度提升，也可能使整体模型的准确度降低。从而也说明了，该参数更适合进行粗粒度的调整。在训练的现阶段，“抖动”现象的发生说明，此时对该参数的调整已不太合适了。

　　对“分裂所需的最小样本数”（min_samples_split）以1为单位，设定取值范围为2到11，得到调参的结果：

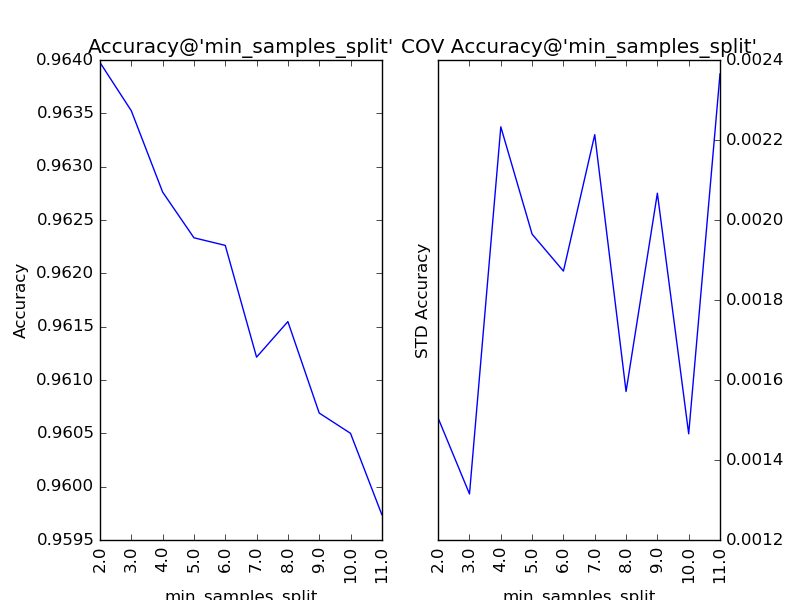
　　我们看到，随着分裂所需的最小样本数的增加，子模型的结构变得越来越简单，理论上来说，首先应当因方差减小导致整体模型的准确度提升。但是，在训练的现阶段，子模型的偏差增大的幅度比方差减小的幅度更大，所以整体模型的准确度持续下降。该参数的默认值为2，调参后，最优解保持2不变。

　　对“叶节点最小样本数”（min_samples_leaf）以1为单位，设定取值范围为1到10，得到调参结果如下：

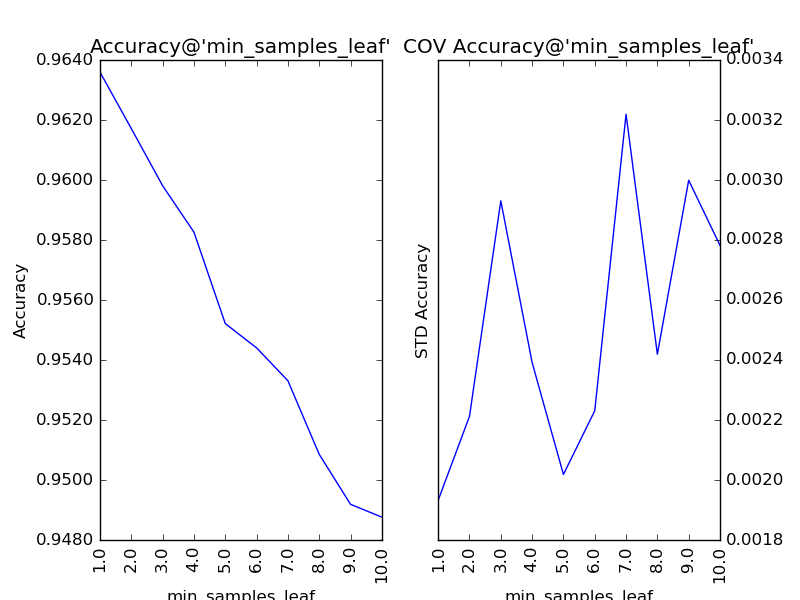
　　同“分裂所需的最小样本数”，该参数也在调参后，保持最优解1不变。

　　对“最大叶节点数”（max_leaf_nodes）以100为单位，设定取值范围为2500到3400，得到调参结果如下：

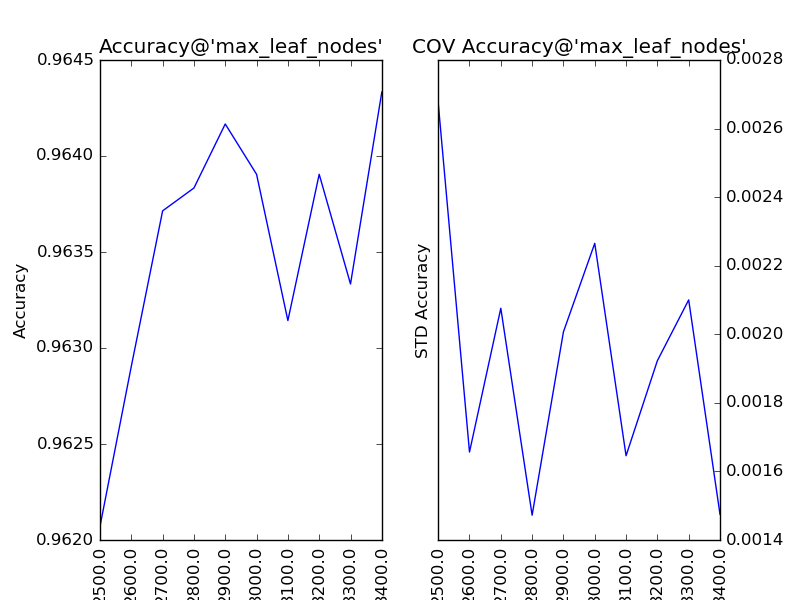
　　类似于“最大深度”，该参数的增大会带来模型准确的提升，可是由于后期“不规律”的抖动，我们暂时不进行处理。

　　通过对以上参数的调参情况，我们可以总结如下：

参数	默认值准确度	调整后最佳准确度	提升幅度
分裂条件（criterion）	0.964023809524	0.964023809524	0
分裂时参与判断的最大特征数（max_feature）	0.963380952381	0.964428571429	0.00104762
最大深度（max_depth）			抖动
分裂所需的最小样本数（min_samples_split）	0.963976190476	0.963976190476	0
叶节点最小样本数（min_samples_leaf）	0.963595238095	0.963595238095	0
最大叶节点数（max_leaf_nodes）			抖动

　　接下来，我们固定分裂时参与判断的最大特征（max_features）为38，在Kaggle上提交一次结果：0.96671，比上一次调参好了0.00171，基本与我们预期的提升效果一致。

　　还需要继续下一轮坐标下降式调参吗？一般来说没有太大的必要，在本轮中出现了两个发生抖动现象的参数，而其他参数的调整均没有提升整体模型的性能。还是得老调重弹：数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。在DR竞赛中，与其期待通过对RandomForestClassifier调参来进一步提升整体模型的性能，不如挖掘出更有价值的特征，或者使用自带特征挖掘技能的模型（正如此题，图分类的问题更适合用神经网络来学习）。但是，在这里，我们还是可以自信地说，通过贪心的坐标下降法，比那些用网格搜索法穷举所有参数组合，自以为得到最优解的朋友们更进了一步。

2.3.2 Gradient Tree Boosting调参案例：Hackathon3.x

　　在这里，我们选取Analytics Vidhya上的Hackathon3.x作为案例来演示对GradientBoostingClassifier调参的过程。

2.3.2.1 调整过程影响类参数

　　GradientBoostingClassifier的过程影响类参数有“子模型数”（n_estimators）和“学习率”（learning_rate），我们可以使用GridSearchCV找到关于这两个参数的最优解。慢着！这里留了一个很大的陷阱：“子模型数”和“学习率”带来的性能提升是不均衡的，在前期会比较高，在后期会比较低，如果一开始我们将这两个参数调成最优，这样很容易陷入一个“局部最优解”。在目标函数都不确定的情况下（如是否凸？），谈局部最优解就是耍流氓，本文中“局部最优解”指的是调整各参数都无明显性能提升的一种状态，所以打了引号。下图中展示了这个两个参数的调参结果：

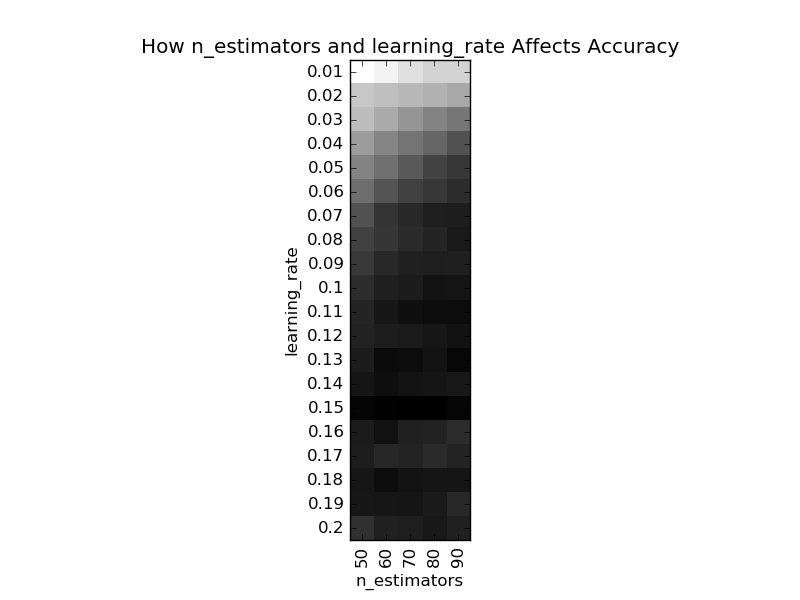
# 图中颜色越深表示整体模型的性能越高

　　在此，我们先直觉地选择“子模型数”为60，“学习率”为0.1，此时的整体模型性能（平均准确度为0.8253）不是最好，但是也不差，良好水准。

2.3.2.2 调整子模型影响类参数

　　对子模型影响类参数的调整与Random Forest类似。最终我们对参数的调整如下：

子模型数 n_estimators	学习率 learning_rate	叶节点最小样本数 min_samples_leaf	最大深度 max_depth	子采样率 subsample	分裂时参与判断的最大特征数 max_feature
60	0.1	12	4	0.77	10

　　到此，整体模型性能为0.8313，与workbench（0.8253）相比，提升了约0.006。

2.3.2.3 杀一记回马枪

　　还记得一开始我们对“子模型数”（n_estimators）和“学习率”（learning_rate）手下留情了吗？现在我们可以回过头来，调整这两个参数，调整的方法为成倍地放大“子模型数”，对应成倍地缩小“学习率”（learning_rate）。通过该方法，本例中整体模型性能又提升了约0.002。

2.4 “局部最优解”

　　目前来说，在调参工作中，广泛使用的仍是一些经验法则。Aarshay Jain对Gradient Tree Boosting总结了一套调参方法，其核心思想在于：对过程影响类参数进行调整，毕竟它们对整体模型性能的影响最大，然后依据经验，在其他参数中选择对整体模型性能影响最大的参数，进行下一步调参。这种方法的关键是依照对整体模型性能的影响力给参数排序，然后按照该顺序对的参数进行调整。如何衡量参数对整体模型性能的影响力呢？基于经验，Aarshay提出他的见解：“最大叶节点数”（max_leaf_nodes）和“最大树深度”（max_depth）对整体模型性能的影响大于“分裂所需最小样本数”（min_samples_split）、“叶节点最小样本数”（min_samples_leaf）及“叶节点最小权重总值”（min_weight_fraction_leaf），而“分裂时考虑的最大特征数”（max_features）的影响力最小。

　　Aarshay提出的方法和贪心的坐标下降法最大的区别在于前者在调参之前就依照对整体模型性能的影响力给参数排序，而后者是一种“很自然”的贪心过程。还记得2.3.2.1小节中我们讨论过“子模型数”（n_estimators）和“学习率”（learning_rate）的调参问题吗？同理，贪心的坐标下降法容易陷入“局部最优解”。对Random Forest调参时会稍微好一点，因为当“子模型数”调到最佳状态时，有时就只剩下诸如““分裂时参与判断的最大特征数”等Aarshay认为影响力最小的参数可调了。但是，对Gradient Tree Boosting调参时，遇到“局部最优解”的可能性就大得多。

　　Aarshay同样对Hackathon3.x进行了调参试验，由于特征提取方式的差异，参数赋值相同的情况下，本文的整体模型性能仍与其相差0.007左右（唉，不得不再说一次，特征工程真的很重要）。首先，在过程影响类参数的选择上，Aarshay的方法与贪心的坐标下降法均选择了“子模型数”为60，“学习率”为0.1。接下来，Aarshay按照其定义的参数对整体模型性能的影响力，按序依次对参数进行调整。当子模型影响类参数确定完成后，Aarshay的方法提升了约0.008的整体模型性能，略胜于贪心的坐标下降法的0.006。但是，回过头来继续调试“子模型数”和“学习率”之后，Aarshay的方法又提升了约0.01的整体模型性能，远胜于贪心的坐标下降法的0.002。

　　诶！诶！诶！少侠请住手！你说我为什么要在这篇博文中介绍这种“无用”的贪心的坐标下降法？首先，这种方法很容易凭直觉就想到。人们往往花了很多的时间去搞懂模型的参数是什么含义，对整体模型性能有什么影响，搞懂这些已经不易了，所以接下来很多人选择了最直观的贪心的坐标下降法。通过一个实例，我们更容易记住这种方法的局限性。除了作为反面教材，贪心的坐标下降法就没有意义了吗？不难看到，Aarshay的方法仍有改进的地方，在依次对参数进行调整时，还是需要像贪心的坐标下降法中一样对参数的“动态”影响力进行分析一下，如果这种影响力是“抖动”的，可有可无的，那么我们就不需要对该参数进行调整。

2.5 类别不均衡的陷阱

　　哈哈哈，这篇博文再次留了个陷阱，此段文字并不是跟全文一起发布！有人要说了，按照我的描述，Aarshay的调参试验不可再现啊！其实，我故意没说Aarshay的另一个关键处理：调参前的参数初始值。因为Hackathon3.x是一个类别不均衡的问题，所以如果直接先调试“最大深度”（max_depth），会发现其会保持默认值3作为最优解，而后面的调参中，“分裂所需最小样本数”（min_samples_split）、“叶节点最小样本数”（min_samples_leaf）再怎么调都没有很大作用。这是因为，正例样本远远小于反例，所以在低深度时，子模型就可能已经对正例过拟合了。所以，在类别不均衡时，只有先确定“叶节点最小样本数”（min_samples_leaf），再确定“分裂所需最小样本数”（min_samples_split），才能确定“最大深度”。而Aarshay设定的初始值，则以经验和直觉避开了这个险恶的陷阱。

　　如果实在觉得经验和直觉不靠谱，我还尝试了一种策略：首先，我们需要初步地调一次“子采样率”（subsample）和“分裂时考虑的最大特征数”（max_features），在此基础上依次调好“叶节点最小样本数”（min_samples_leaf）、“分裂所需最小样本数”（min_samples_split）以及“最大深度”（max_depth）。然后，按照Aarshay的方法，按影响力从大到小再调一次。通过这种方法，整体模型性能在未等比缩放过程影响类参数前，已达到约0.8352左右，比workbench相比，提升了约0.1，与Aarshay的调参试验差不多，甚至更好一点点。

　　回过头来，我们再次看看贪心的坐标下降法是怎么掉入这个陷阱的。在确定过程影响类参数后，贪心的坐标下降法按照“动态”的对整体模型性能的影响力大小，选择了“叶节点最小样本数”进行调参。这一步看似和上一段的描述是一致的，但是，一般来说，含随机性（“子采样率”和“分裂时考虑的最大特征数”先初步调过）的“叶节点最小样本数”要大于无随机性。举个例来说，因为增加了随机性，导致了子采样后，某子样本中只有一个正例，且其可以通过唯一的特征将其分类，但是这个特征并不是所有正例的共性，所以此时就要求“叶节点最小样本数”需要比无随机性时大。对贪心的坐标下降来说，“子采样率”和“分裂时考虑的最大特征数”在当下，对整体模型性能的影响比不上“叶节点最小样本数”，所以栽了个大跟头。

---

 

3 总结

　　在这篇博文中，我一反常态，花了大部分时间去试验和说明一个有瑕疵的方案。数据挖掘的工作中的方法和技巧，有很大一部分暂时还未被严谨地证明，所以有很大部分人，特别是刚入门的小青年们（也包括曾经的我），误以为其是一门玄学。实际上，尽管没有被严谨地证明，我们还是可以通过试验、分析，特别是与现有方法进行对比，得到一个近似的合理性论证。

　　另外，小伙伴们你们有什么独到的调参方法吗？请不要有丝毫吝啬，狠狠地将你们的独门绝技全释放在我身上吧，请大胆留言，残酷批评！

---

 

4 参考资料

1. 《使用sklearn进行集成学习——理论》

2. Complete Guide to Parameter Tuning in Gradient Boosting (GBM) in Python

3. 坐标下降法
4. Digit Recognizer
5. Hackathon3.x