【每日一题】20250405
【每日一题】
-
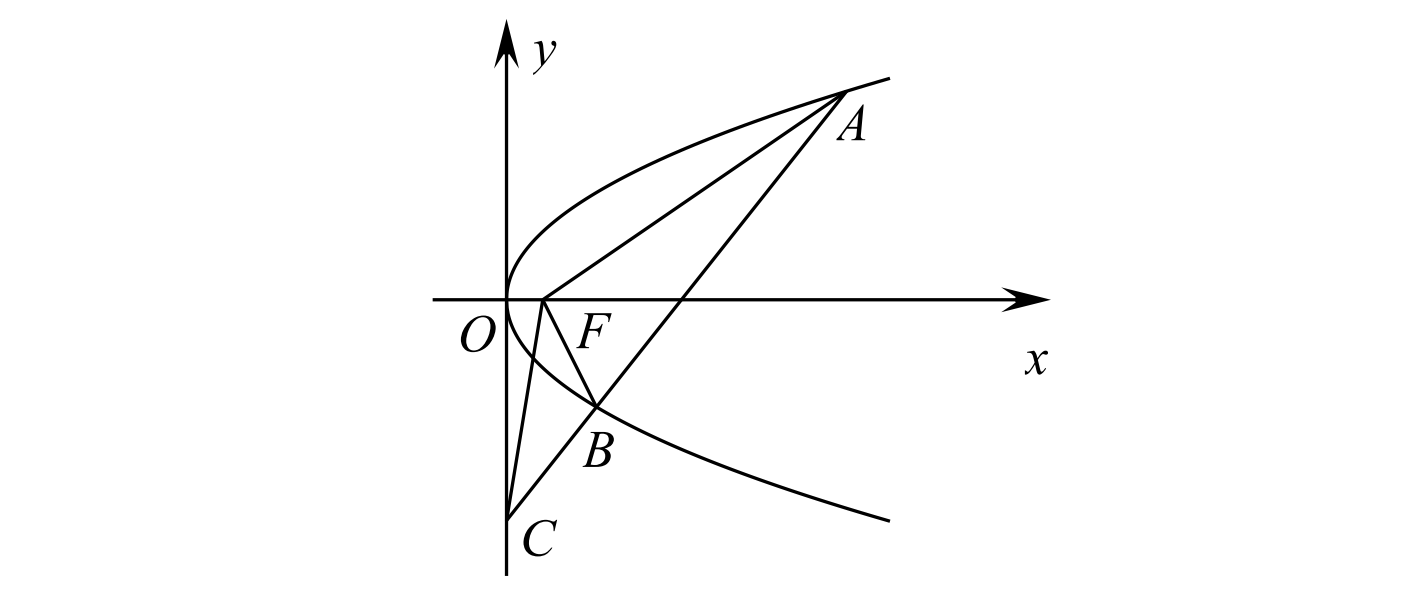
如图,设抛物线 \(y^2=4x\) 的焦点为 \(F\),不经过焦点的直线上有三个不同的点 \(A\),\(B\),\(C\),其中点\(A\),\(B\) 在抛物线上,点 \(C\) 在 \(y\) 轴上,则 \(\triangle BCF\) 与 \(\triangle ACF\) 的面积之比为
A. \(\displaystyle \frac{|BF|-1}{|AF|-1}\)
B. \(\displaystyle \frac{\left|BF\right|^2-1}{\left|AF\right|^2-1}\)
C. \(\displaystyle \frac {\left | BF\right | + 1}{\left | AF\right | + 1}\)
D. \(\displaystyle \frac{\left|BF\right|^2+1}{\left|AF\right|^2+1}\)
![image]()
-
在下面一段命题中有多处错误,请找出错误并进行改正.(正确修改命题中的全部错误得满分,否则每正确修改一处错误得 \(1\) 分,错误修改不得分)
\(\hspace{0.7cm}\)设随机变量 \(X\) 服从正态分布 \(N(10,\sigma^2)\),则 \(P(X=10)=0\).当 \(\sigma\) 增大时,\(P(X \leqslant 9.9)\) 增大;当 \(\sigma\) 减小时,\(P(9.9\leqslant X\leqslant 10.1)\) 减小;无论 \(\sigma\) 如何变化,\(P(9.9\leqslant X)>0.5\) 均成立;无论 \(\sigma\) 如何变化, \(P(9.9\leqslant X)>P(X\leqslant 10.1)\) 均成立;无论 \(\sigma\) 如何变化,\(P(9.9\leqslant X\leqslant 10.2)<P(10.0\leqslant X\leqslant 10.3)\) 均成立.
答:_______________________________. -
在平面直角坐标系 \(xOy\) 中,\(A\) 为直线 \(l\):\(y=2x\) 上在第一象限内的点,\(B(5,0)\),以 \(AB\) 为直径的圆 \(C\) 与直线 \(l\) 交于另一点 \(D\).若 \(\overrightarrow {AB}\cdot \overrightarrow {CD}= 0\),则点 \(A\) 的横坐标为 __________.
[试题来源:2015年浙江卷,原创,2018年江苏卷]
【每日一言】
我很早就明白,如果自己不千方百计地独立,就什么也做不了。 -《日暮时分》黄皙英

【学生撰写过程】

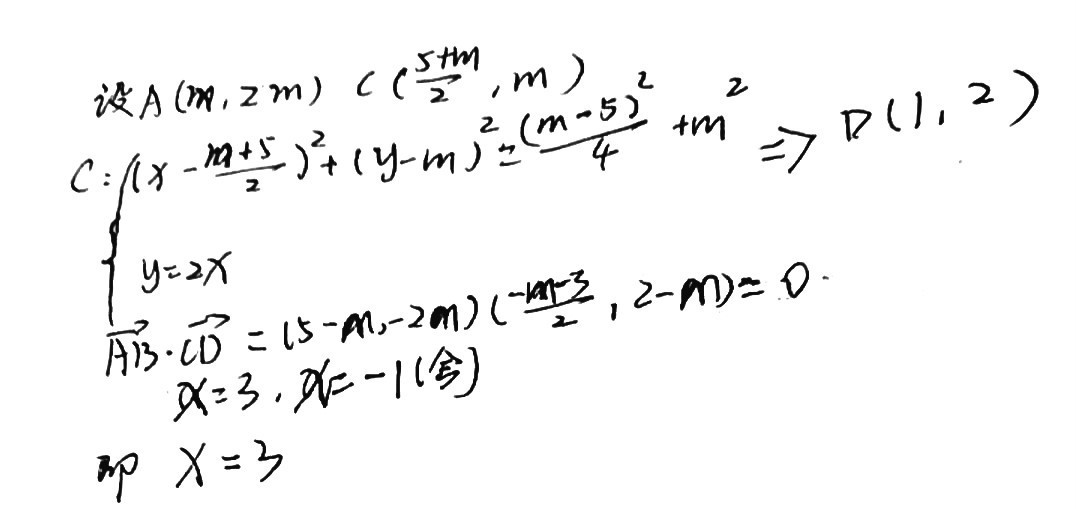
【答案】

未完待续~
2025-04-05 13:11:09 星期六


 我很早就明白,如果自己不千方百计地独立,就什么也做不了。
我很早就明白,如果自己不千方百计地独立,就什么也做不了。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号