【每日一题】20250320

【每日一题】

1. 已知等比数列 \(\{a_n\}\) 的公比为 \(2\)，且 \(a_i>0(i=1,2,\cdots)\)，\(a_3a_{11}=16\)，则 \(\log_2a_{10}=\)
   A. \(4\)
   B. \(5\)
   C. \(6\)
   D. \(7\)

2. 设集合 \(A=\{1,2,3,4,5,6\}\)，\(B=\{4,5,6,7\}\)，则满足 \(S\subseteq A\) 且 \(S\cap B\neq\varnothing\) 的集合 \(S\) 的个数为
   A. \(8\)
   B. \(49\)
   C. \(56\)
   D. \(57\)

3. （多选）已知双曲线 \(\Gamma\) 的一条渐近线方程为 \(\displaystyle y=-\frac{\sqrt{2}}{2}x\)，则 \(\Gamma\) 的方程可能为

选项	内容	选项	内容
A	\(\displaystyle \frac{x^2}2-y^2=1\)	I	\(\displaystyle \frac{y^2}2-x^2=1\)
B	\(\displaystyle x^2-\frac{y^2}2=1\)	J	\(\displaystyle y^2-\frac{x^2}2=1\)
C	\(\displaystyle 2x^2-y^2=1\)	K	\(\displaystyle 2y^2-x^2=1\)
D	\(\displaystyle x^2-2y^2=1\)	L	\(\displaystyle y^2-2x^2=1\)
E	\(\displaystyle \frac {x^2}{\sqrt {2}}- y^2= 1\)	M	\(\displaystyle \frac {y^2}{\sqrt {2}}- x^2= 1\)
F	\(\displaystyle x^2- \frac {y^2}{\sqrt {2}}= 1\)	N	\(\displaystyle y^2- \frac {x^2}{\sqrt {2}}= 1\)
G	\(\displaystyle \sqrt {2}x^{2}-y^{2}= 1\)	O	\(\displaystyle \sqrt {2}y^{2}-x^{2}= 1\)
H	\(\displaystyle x^{2}- \sqrt {2}y^{2}= 1\)	P	\(\displaystyle y^{2}- \sqrt {2}x^{2}= 1\)

[试题来源：2012年安徽卷，2011年安徽卷，原创]

---

【每日一言】

其实我早就发现，人世间最劳心的事，莫过于人与人相互间的伪装和不真诚。人人都戴着面具生活，所以社会生活才会让人这样心力交瘁。 -《大海的礼物：寻找全新的自我》安妮·莫罗·林德伯格

---

【学生撰写过程】

---

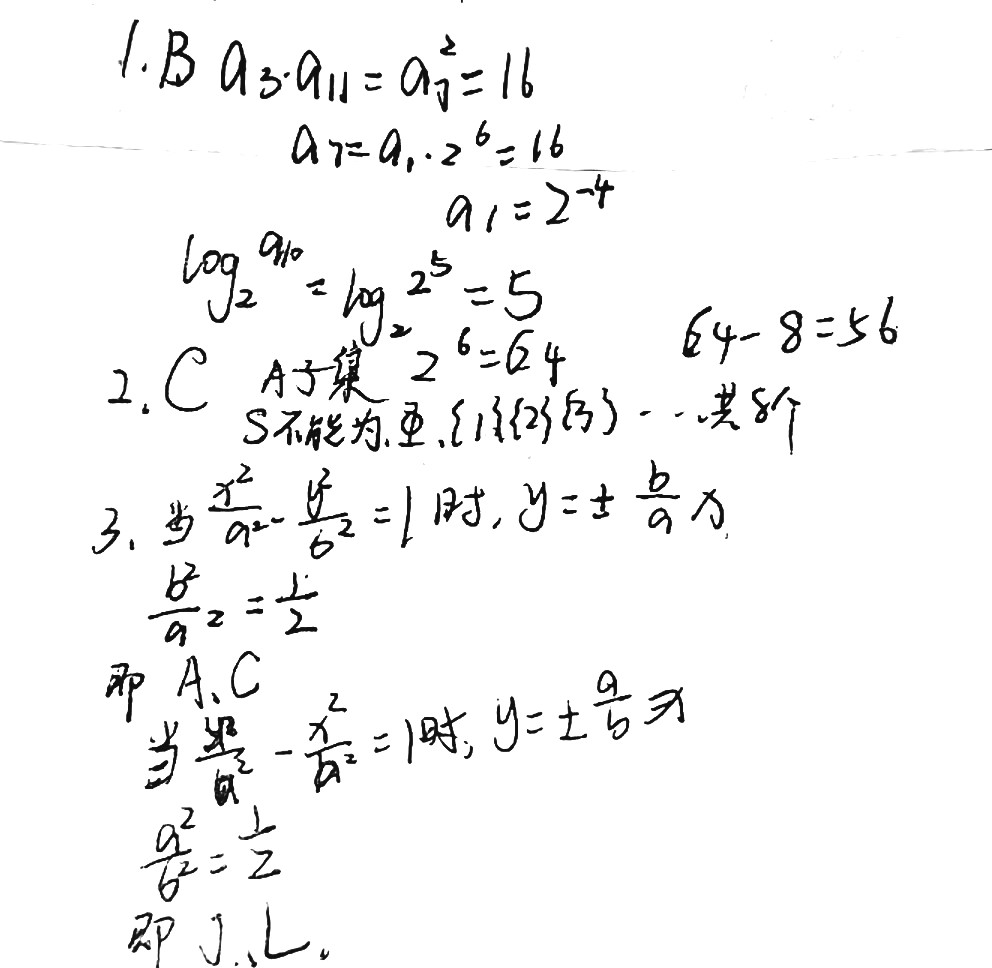
【答案】

---

未完待续~
2025-03-20 12:15:27 星期四