【每日一题】20250317
【每日一题】
-
(不定项)已知曲线 \(C_1\):\(y=\cos x\),\(C_2\):\(\displaystyle y=\sin(2x+\frac{2\pi}{3})\).
(1) 下列结论正确的是
A. 把 \(C_1\) 上各点的横坐标伸长到原来的 \(2\) 倍,纵坐标不变,再把得到的曲线向右平移 \(\displaystyle \frac{\pi}{6}\) 个单位长度,得到曲线 \(C_2\)
B. 把 \(C_1\) 上各点的横坐标伸长到原来的 \(2\) 倍,纵坐标不变,再把得到的曲线向左平移 \(\displaystyle \frac{\pi}{6}\) 个单位长度,得到曲线 \(C_2\)
C. 把 \(C_1\) 上各点的横坐标伸长到原来的 \(2\) 倍,纵坐标不变,再把得到的曲线向右平移 \(\displaystyle \frac\pi{12}\) 个单位长度,得到曲线 \(C_2\)
D. 把 \(C_1\) 上各点的横坐标伸长到原来的 \(2\) 倍,纵坐标不变,再把得到的曲线向左平移 \(\displaystyle \frac\pi{12}\) 个单位长度,得到曲线 \(C_2\)
E. 把 \(C_1\) 上各点的横坐标缩短到原来的 \(\displaystyle \frac12\) 倍,纵坐标不变,再把得到的曲线向右平移 \(\displaystyle \frac\pi6\)个单位长度,得到曲线 \(C_2\)
F. 把 \(C_1\) 上各点的横坐标缩短到原来的 \(\displaystyle \frac12\) 倍,纵坐标不变,再把得到的曲线向左平移 \(\displaystyle \frac\pi6\)个单位长度,得到曲线 \(C_2\)
G. 把 \(C_1\) 上各点的横坐标缩短到原来的 \(\displaystyle \frac12\) 倍,纵坐标不变,再把得到的曲线向右平移 \(\displaystyle \frac\pi{12}\) 个单位长度,得到曲线 \(C_2\)
H. 把 \(C_1\) 上各点的横坐标缩短到原来的 \(\displaystyle \frac12\) 倍,纵坐标不变,再把得到的曲线向左平移 \(\displaystyle \frac\pi{12}\) 个单位长度,得到曲线 \(C_2\)
I. 把 \(C_1\) 向右平移 \(\displaystyle \frac\pi{6}\) 个单位长度,纵坐标不变,再把得到的曲线上各点的横坐标伸长到原来的 \(2\) 倍,得到曲线 \(C_2\)
J. 把 \(C_1\) 向左平移 \(\displaystyle \frac\pi{6}\) 个单位长度,纵坐标不变,再把得到的曲线上各点的横坐标伸长到原来的 \(2\) 倍,得到曲线 \(C_2\)
K. 把 \(C_1\) 向右平移 \(\displaystyle \frac\pi{3}\) 个单位长度,纵坐标不变,再把得到的曲线上各点的横坐标伸长到原来的 \(2\) 倍,得到曲线 \(C_2\)
L. 把 \(C_1\) 向左平移 \(\displaystyle \frac\pi{3}\) 个单位长度,纵坐标不变,再把得到的曲线上各点的横坐标伸长到原来的 \(2\) 倍,得到曲线 \(C_2\)
M. 把 \(C_1\) 向右平移 \(\displaystyle \frac\pi{6}\) 个单位长度,纵坐标不变,再把得到的曲线上各点的横坐标缩短到原来的 \(\displaystyle \frac12\) 倍,得到曲线 \(C_2\)
N. 把 \(C_1\) 向左平移 \(\displaystyle \frac\pi{6}\) 个单位长度,纵坐标不变,再把得到的曲线上各点的横坐标缩短到原来的 \(\displaystyle \frac12\) 倍,得到曲线 \(C_2\)
O. 把 \(C_1\) 向右平移 \(\displaystyle \frac\pi{3}\) 个单位长度,纵坐标不变,再把得到的曲线上各点的横坐标缩短到原来的 \(\displaystyle \frac12\) 倍,得到曲线 \(C_2\)
P. 把 \(C_1\) 向左平移 \(\displaystyle \frac\pi{3}\) 个单位长度,纵坐标不变,再把得到的曲线上各点的横坐标缩短到原来的 \(\displaystyle \frac12\) 倍,得到曲线 \(C_2\)
(2) 根据 (1) 中选项的格式,试写出两种由曲线 \(C_2\) 变换为 \(C_1\) 的变换方式. -
(多选)已知在三棱锥 \(P-ABC\) 中,\(PA\bot\) 平面 \(ABC\) ,\(\angle ACB=90^{\circ}\),\(PA=AC=BC\),\(E\) 为 \(AB\) 的中点,则在下列命题中正确的为
A. 异面直线 \(PB\) 与 \(CE\) 所成角的正切值不存在
B. 在三棱锥 \(P-ABC\) 的六条棱中,最长的棱为 \(PB\)
C. 在三棱锥 \(P-ABC\) 的四个面中,属于直角三角形面的有且仅有 \(3\) 个
D. 若三棱锥 \(P-ABC\) 的所有顶点都在同一个球面上,则其球心位于 \(E\) 点处
E. 若三棱锥 \(P-ABC\) 的所有顶点都在同一个球面上,则其球心位于 \(\triangle PAB\) 的内心处
F. 若三棱锥 \(P-ABC\) 的所有顶点都在同一个球面上,且 \(PA=a\),则该球面的半径为 \(\displaystyle \frac{\sqrt5}2a\) -
已知椭圆 \(C\):\(\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\),点 \(P\) 为椭圆的两条相互垂直的切线相交点,求点 \(P\) 的轨迹方程.
[试题来源:2017年全国 I 卷(改编),原创,未知]
【每日一言】
小时候以为人生是踏歌而行,后来才明白其实脚下踏着的是利刃和刀锋。-《她穿过了暴雨》独木舟

【学生撰写过程】

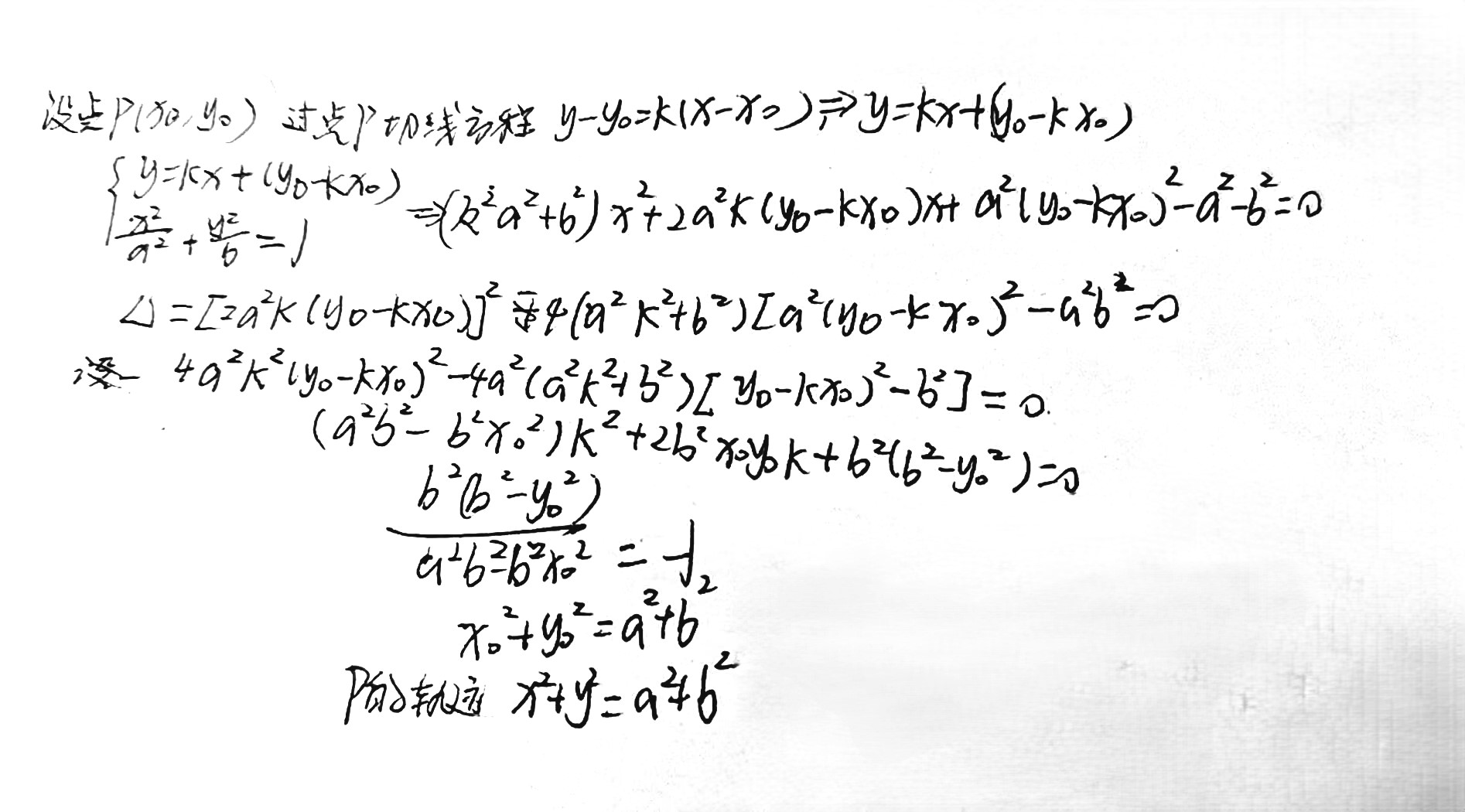
【答案】

未完待续~
2025-03-17 12:18:16 星期一


 小时候以为人生是踏歌而行,后来才明白其实脚下踏着的是利刃和刀锋。
小时候以为人生是踏歌而行,后来才明白其实脚下踏着的是利刃和刀锋。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号