【每日一题】20250226
【每日一题】
1.(15分)
\(\hspace{0.7cm}\)已知数列 \(\{a_n \}\) 和 \(\{b_n \}\) 满足 \(a_1a_2a_3\cdots a_n=(\sqrt{2})^{b_n}\).若 \(\{a_n \}\) 为等比数列,且 \(a_1=2\),\(b_3=6+b_2\).
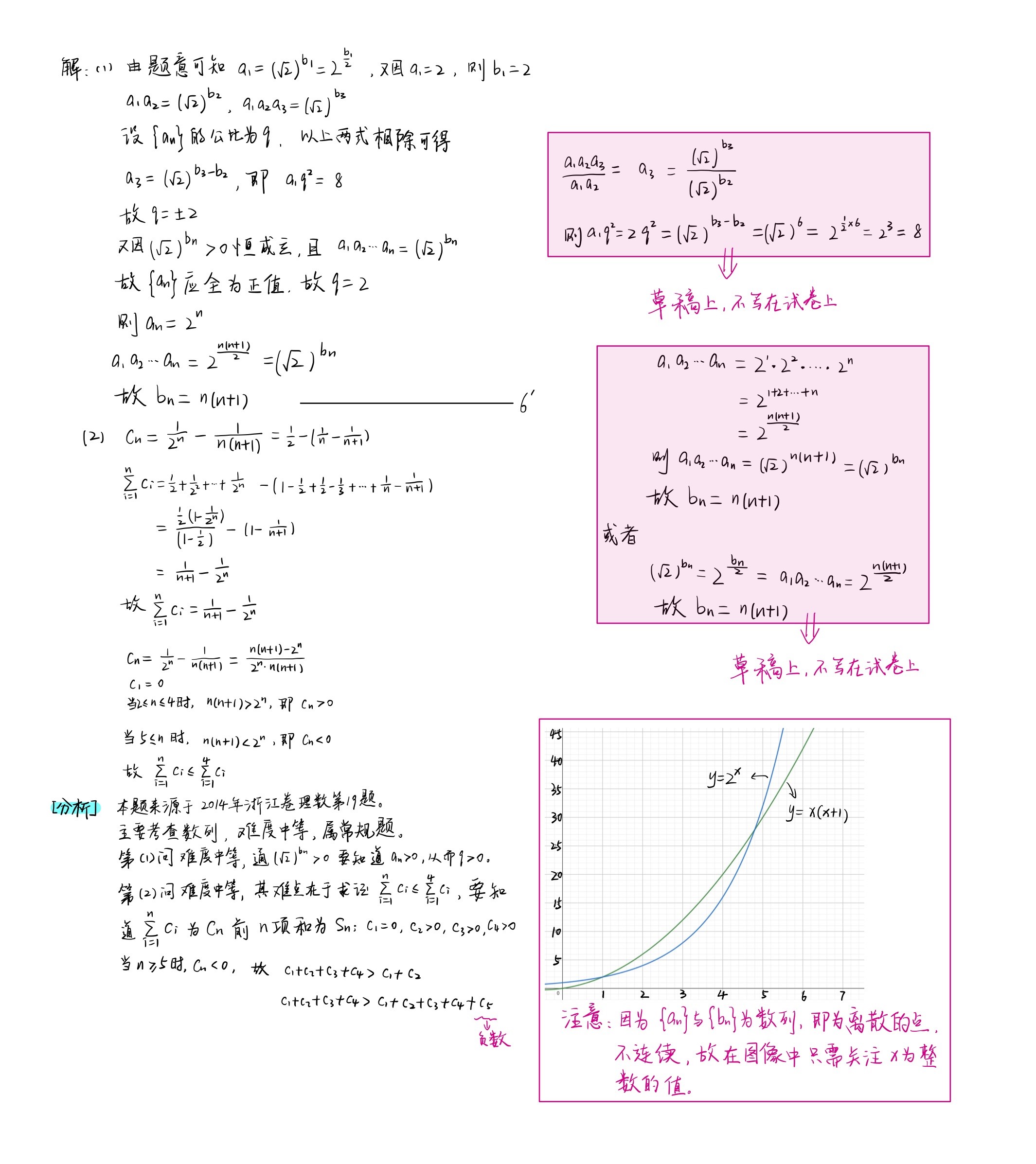
\(\hspace{0.7cm}\)(1)求 \(\{a_n\}\) 与 \(\{b_n\}\) 的通项公式;
\(\hspace{0.7cm}\)(2)设 \(\displaystyle c_n=\frac{1}{a_n}-\frac{1}{b_n}(n\in\mathbf{N}^\ast)\),求 \(\displaystyle\sum_{i=1}^nc_i\),并证明:\(\displaystyle\sum_{i=1}^nc_i \leqslant \sum_{i=1}^4c_i\).
[试题来源:2014年浙江卷]
【每日一言】
人,不是什么事都可以干的。很多时候,欲望自缚,即精神自救。 -《做一个精神明亮的人》王开岭

【学生撰写过程】
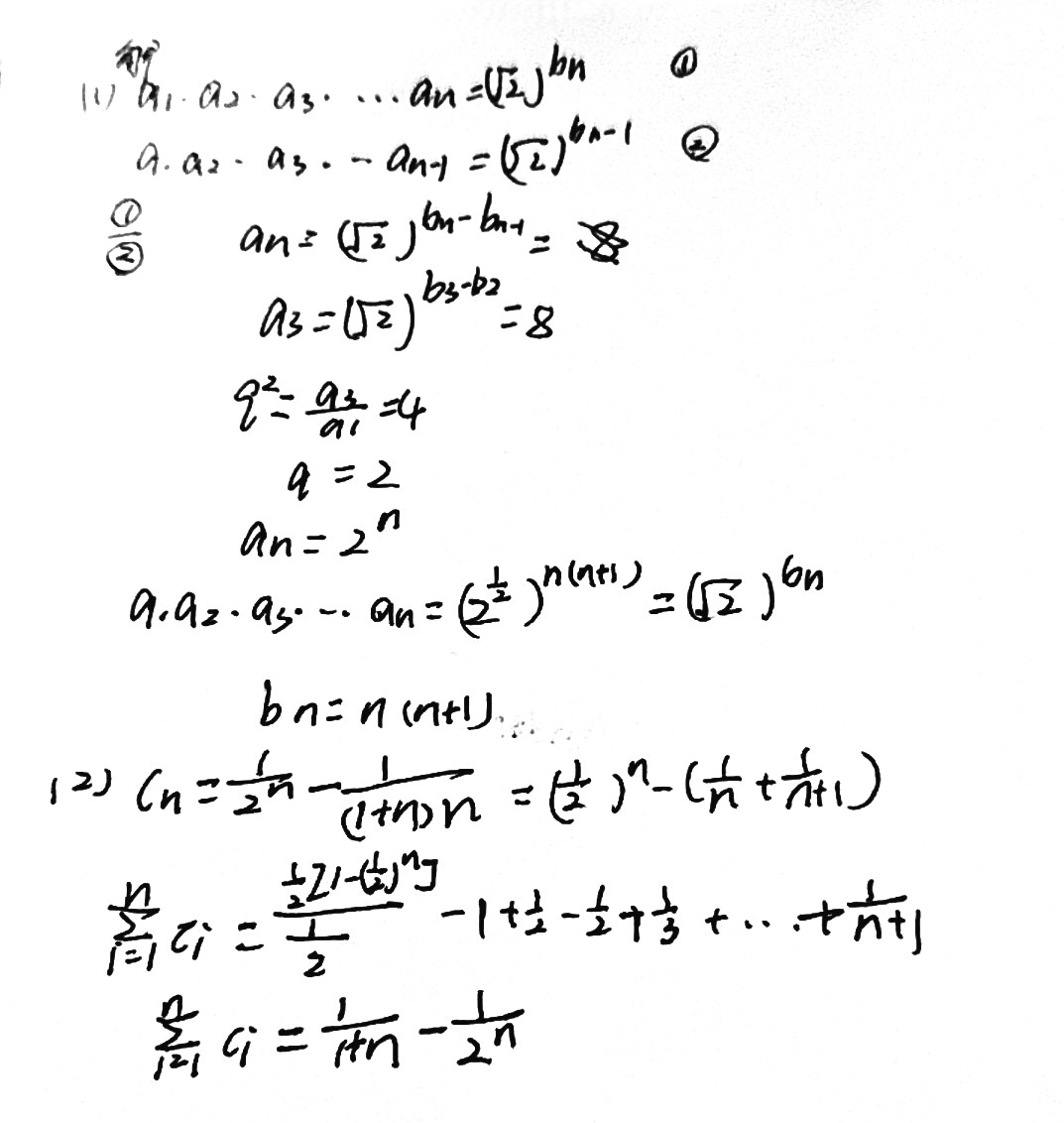
【答案】

未完待续~
2025-02-26 11:45:49 星期三


 人,不是什么事都可以干的。很多时候,欲望自缚,即精神自救。
人,不是什么事都可以干的。很多时候,欲望自缚,即精神自救。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号