【每日一题】20250415
【每日一题】
-
已知 \(\odot C\) 与 \(y\) 轴相切于点 \((0,2)\),与 \(x\) 轴交于 \(A\),\(B\) 两点,且 \(|AB|=4\),则 \(\odot C\) 的标准方程为_________.
-
(5分)
\(\hspace{0.7cm}\)已知函数\(\displaystyle f(x)=\ln (-2x^3+5^2)-\log_9{(3x^2-2)}+2e^{-3x^2}+5^{-3x}-(3x-5)^6(2-x)^3(6-7x^2)^2,\)求 \(f(x)\) 的导数. -
(13分)
\(\hspace{0.7cm}\)将一个正四面体某正三角形面朝下放在桌面上,此时与桌面所接触的正三角形面表示为初始接触面 \(\alpha\).现任意选择初始接触面 \(\alpha\) 的一边,以此边为转动轴推动正四面体,使得与转动轴相邻的另一面朝下.
\(\hspace{0.7cm}\)(1)定义操作方案如下:重复推动 \(3\) 次的过程中,初始接触面 \(\alpha\) 与桌面接触的次数记为 \(X\).
\(\hspace{0.7cm}\)(i)若对该方案进行 \(1\) 次操作,求 \(X\) 的分布列;
\(\hspace{0.7cm}\)(ii)若对该方案进行 \(20\) 次独立操作,每次操作完毕后均手动将初始接触面 \(\alpha\) 与桌面接触,记 \(Y\) 为 \(X=1\) 的次数.求 \(EY\);
\(\hspace{0.7cm}\)(2)若 \(p_n\) 表示为重复推动 \(n\) 次后,初始接触面 \(\alpha\) 再次与桌面接触的概率.
\(\hspace{0.7cm}\)(i)证明:\(\displaystyle \{p_n-\frac14\}\) 为等比数列;
\(\hspace{0.7cm}\)(ii)求 \(p_n\) 的上限与下限,并说明 \(p_n\) 的变化情况.
[试题来源:2015年湖北卷(改编),原创,1991年东京大学入学考试(改编)]
【每日一言】
一个人要干多少蠢事才能混到中年呢?肯定不止一件两件。 -白菜《屋檐下》

【学生撰写过程】
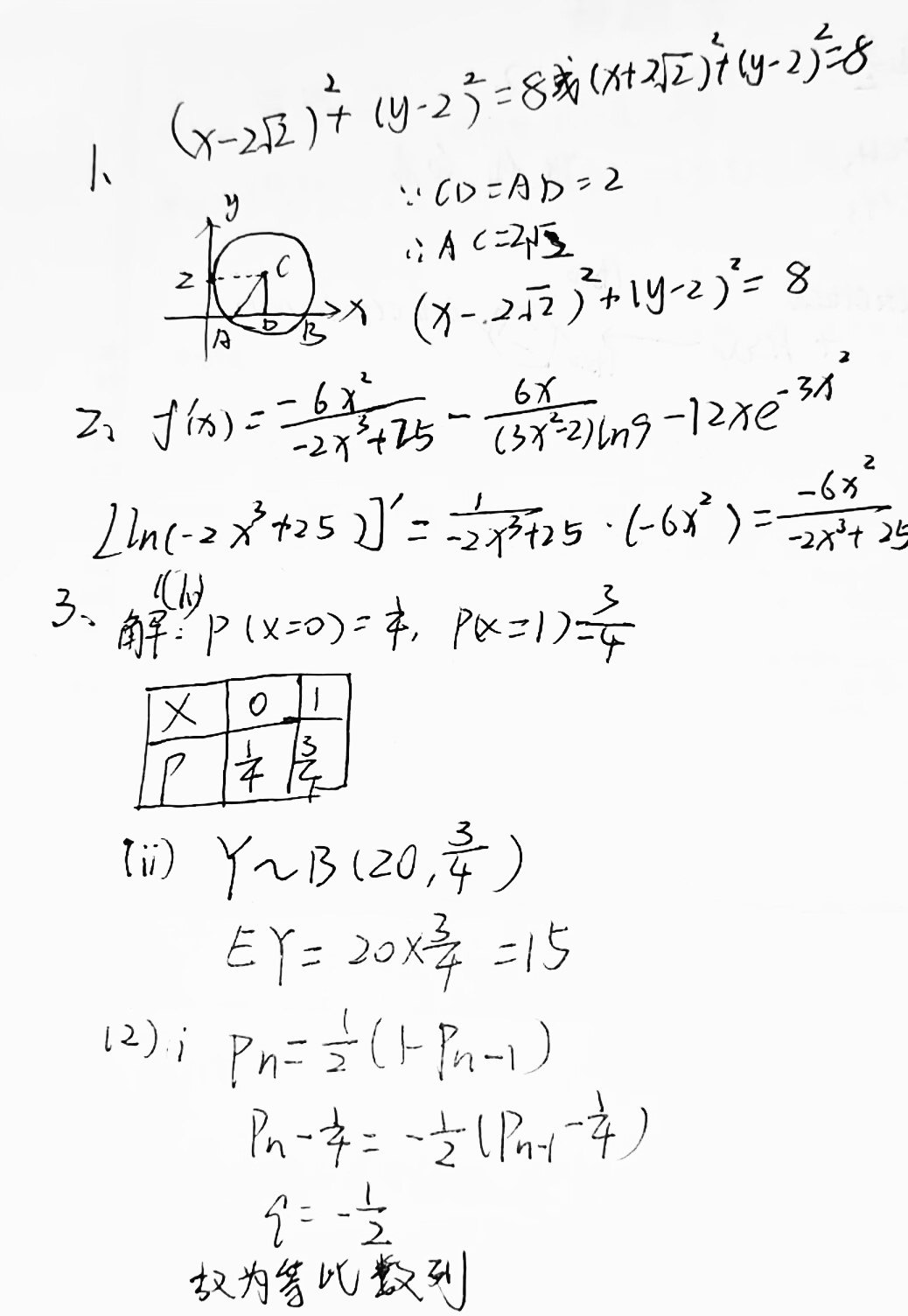
【答案】

未完待续~
2025-04-15 11:28:52 星期二


 一个人要干多少蠢事才能混到中年呢?肯定不止一件两件。
一个人要干多少蠢事才能混到中年呢?肯定不止一件两件。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号