【每日一题】20250220

【每日一题】

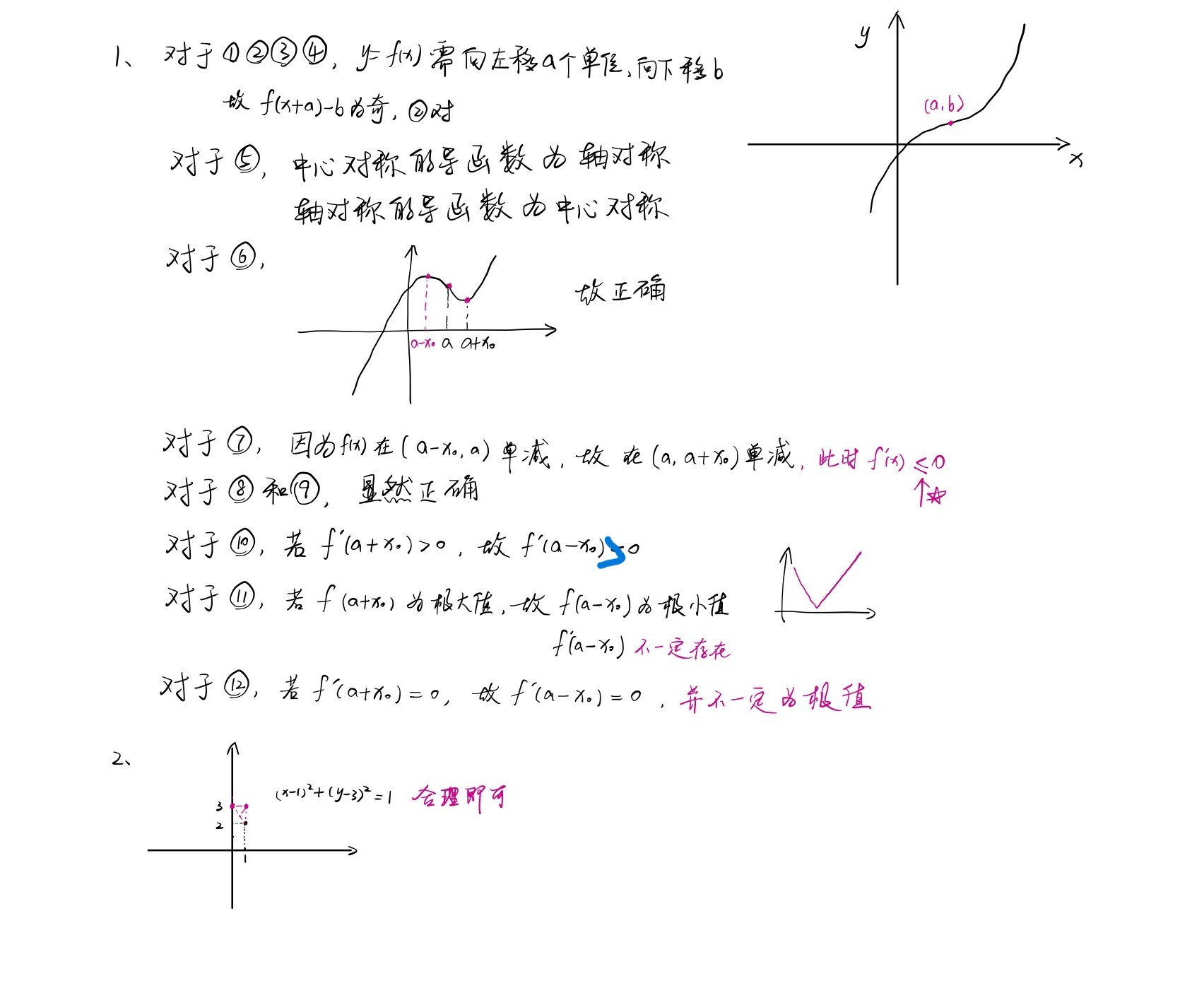
1. 已知曲线 \(y=f(x)\) 为中心对称图形，点 \((a,b)\) 为其对称中心，\(f^{\prime}(x)\) 为 \(f(x)\) 的导数，则下列命题正确的为_________．（写出所有正确命题的编号）
   ① \(f(x-a)-b\) 为奇函数
   ② \(f(x+a)-b\) 为奇函数
   ③ \(f(x-a)\) 为奇函数
   ④ \(f(x+a)\) 为奇函数
   ⑤ 曲线 \(y=f^{\prime}(x)\) 为轴对称图形
   ⑥ 若 \(x=a+x_0\) 为 \(f(x)\) 的极小值点，则 \(x=a-x_0\) 为极大值点
   ⑦ 若函数 \(f(x)\) 在区间 \((a-x_0,a)\) 上单调递减，则当 \(x\in(a,a+x_0)\) 时，\(f^{\prime}(x)>0\)
   ⑧ \(f(a+x)+f(a-x)=2f(a)\)
   ⑨ \(f(a+x)+f(a-x)=2b\)
   ⑩ 若 \(f'(a+x_0)>0\)，则 \(f'(a-x_0)<0\)
   ⑪ 若 \(f(a+x_0)\) 为极大值，则 \(f^{\prime}(a-x_0)=0\)
   ⑫ 若 \(f^{\prime}(a+x_0)=0\)，则 \(x=a-x_0\) 为极值点

2. 已知 \(\odot C\) 与 \(y\) 轴相切，且过点 \((1,2)\)，则 \(\odot C\) 的方程为_________．（写出一个即可）

[试题来源：原创]

---

【每日一言】

你小时候那么向往的东西，等你真正得到它们的时候，似乎并不那么美妙了。 -《绿山墙的安妮》露西．莫德．蒙哥马利

---

【学生撰写过程】

---

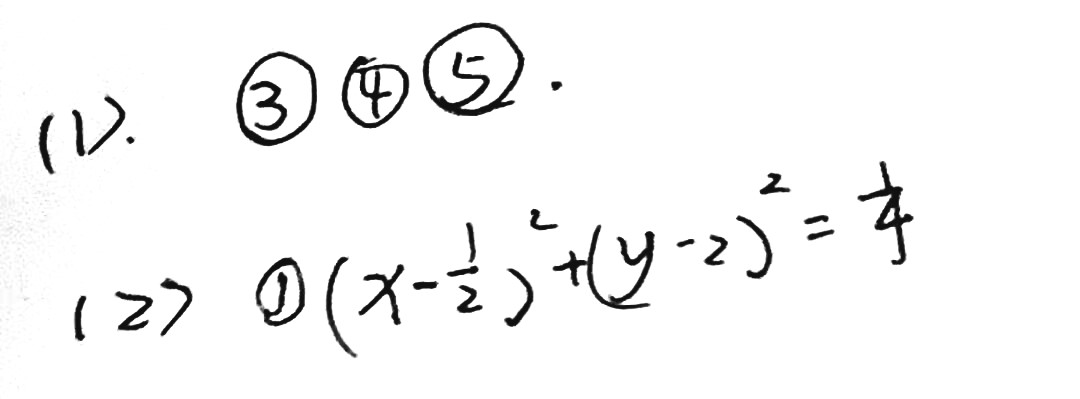
【答案】

---

未完待续~
2025-02-20 13:51:55 星期四