LeetCode-647. 回文子串
LeetCode-647. 回文子串
标签:字符串、动态规划
题目
🚗问题描述
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
🚗问题示例
示例 1:
输入:s = "abc"
输出:3
解释:三个回文子串: "a", "b", "c"示例 2:
输入:s = "aaa"
输出:6
解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
🚗提示
1 <= s.length <= 1000
s 由小写英文字母组成
题解
🚆方法1:暴力遍历算法
问题分析:由题目可知,如果我们要比较回文串,此时对各个子串进行判断,若该子串为回文串,则回文串数目加1。以示例1:s="abc"为例,其子串的所有可能为:"a"、"ab"、"abc"、"b"、"bc"、"c",我们需要挨个判断这些子串是否为回文串。但如果使用这种算法进行判断,时间复杂度为O(n3),这显然不是一个好的算法。下面是这种方法的实现:
class Solution {
public:
bool isCircleString(string s)
{
int begin = 0;
int last = s.length() - 1;
while(begin <= last)
{
if(s[begin] != s[last]) return false;
begin++;
last--;
}
return true;
}
int countSubstrings(string s) {
int n = s.length();
int ret = 0;
for(int i = 0; i < n; i++)
for(int j = i; j < n; j++)
if(isCircleString(s.substr(i, j - i + 1)))
ret++;
return ret;
}
};
🚆方法2:动态规划算法
问题分析:我们可以创建一个二维的dp表,dp[i][j]表示从i位置到j位置的子串是否为回文串。如下图,上表对应的是以i位置开始,j位置结束的子串;下表对应的是i位置开始,j位置结束的子串是否为回文串,下表也就是我们存储的dp表。
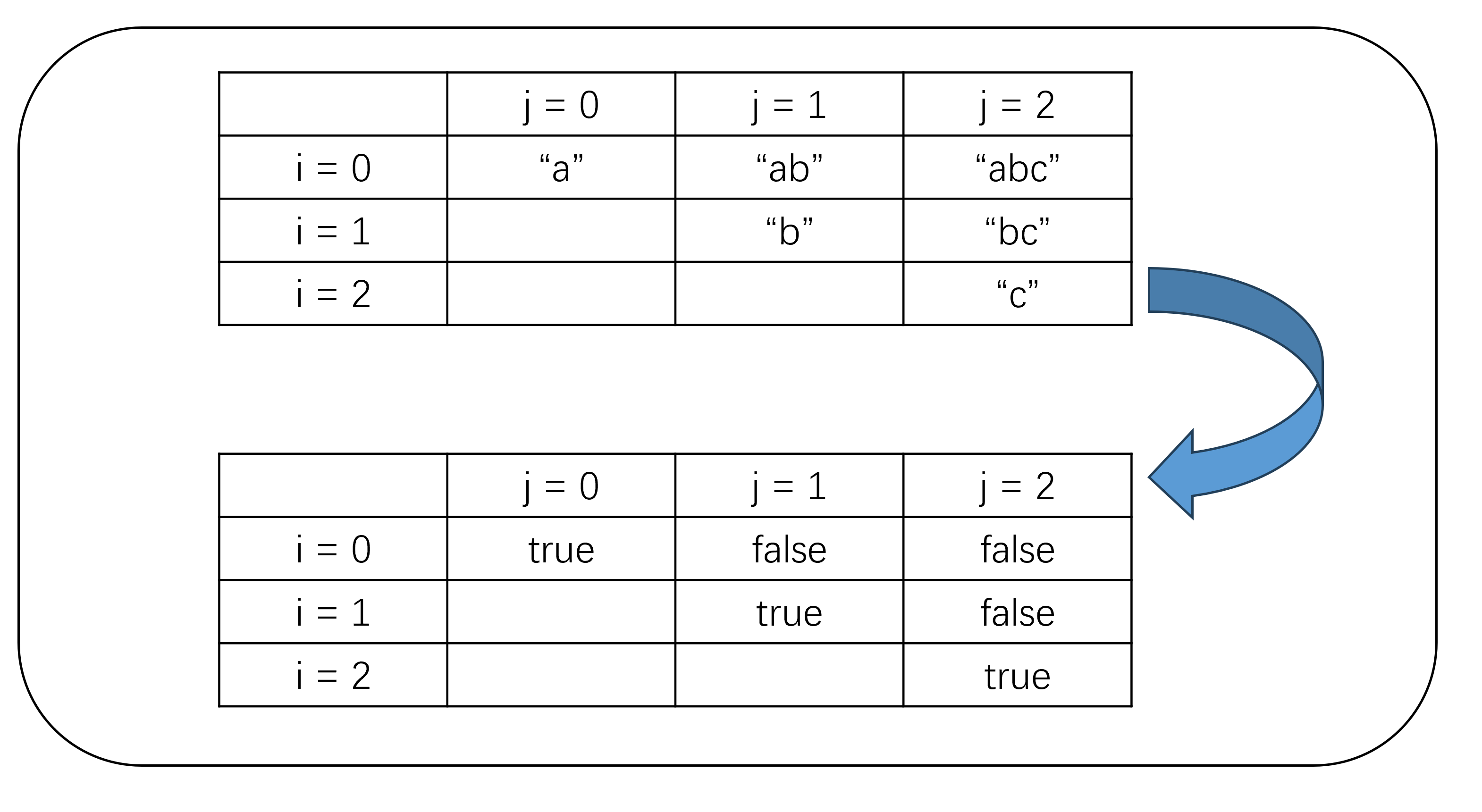
如果单纯拿一个二维数组存储子串是否为回文串,这不是白白浪费空间吗?别急,再看看下面的思路->我们知道,如果i==j,即只有一个字符,那么它一定是回文串;如果s[i] == s[j]&&i+1 == j,即两个相同的字符,它也一定是回文串;若已知s[i+1][j-1]是回文串,如果s[i]==s[j],则该字符串也为回文串。
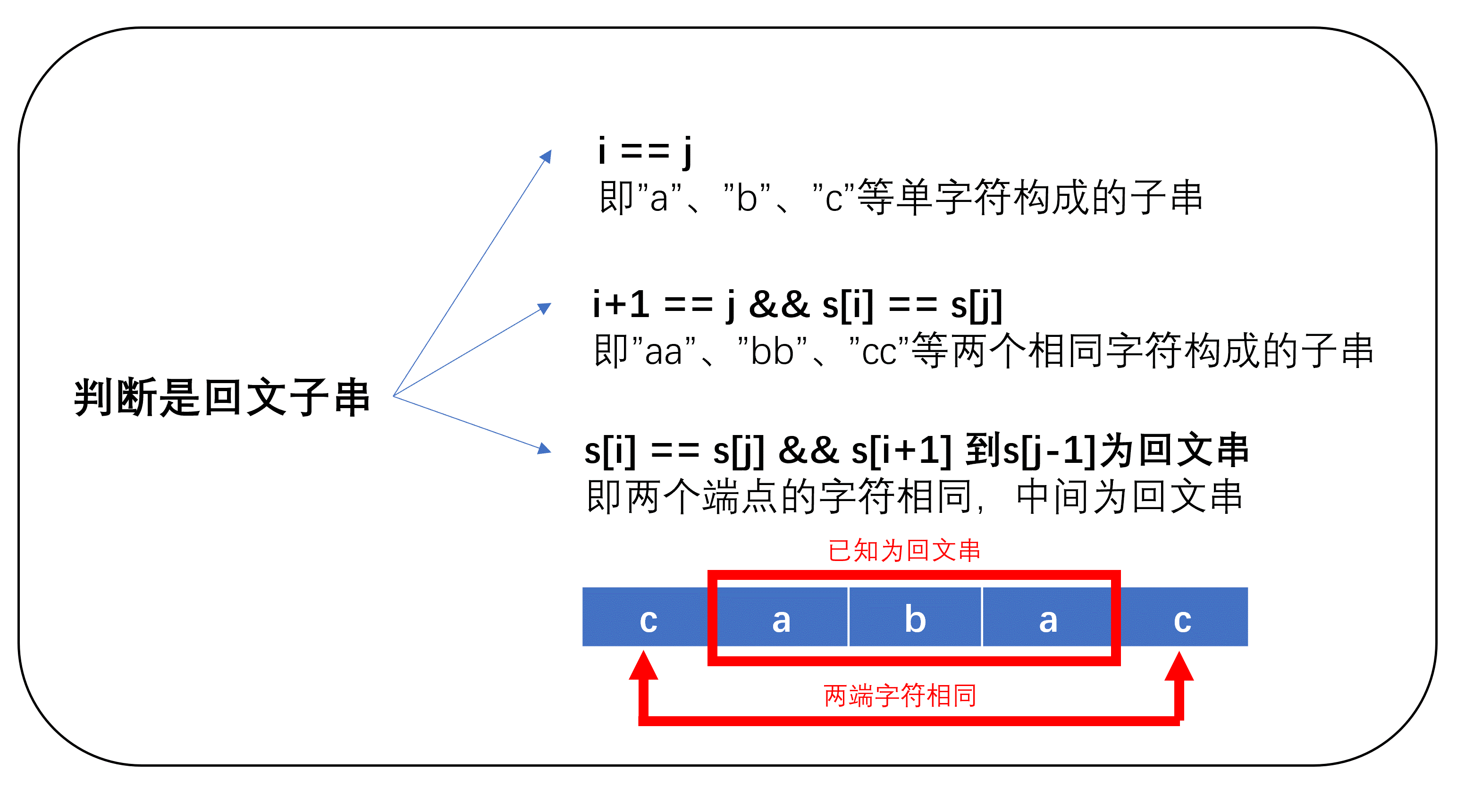
这三个判断条件中,最难满足的是第三个,因为它需要知道s[i+1][j-1]是否为回文串。这应该怎么的出来呢?我们可以通过i和j均从大到小到大的方式,对各个子串进行判断。为什么这么遍历呢?因为在求解s[i][j]时,s[i+1][j-1]已经遍历过了(i+1>i),所以s[i+1][j-1]是否为回文串已经知道了。此时,只需要判断s[i]、s[j]是否相等,即可得到s[i][j]是否为回文串。
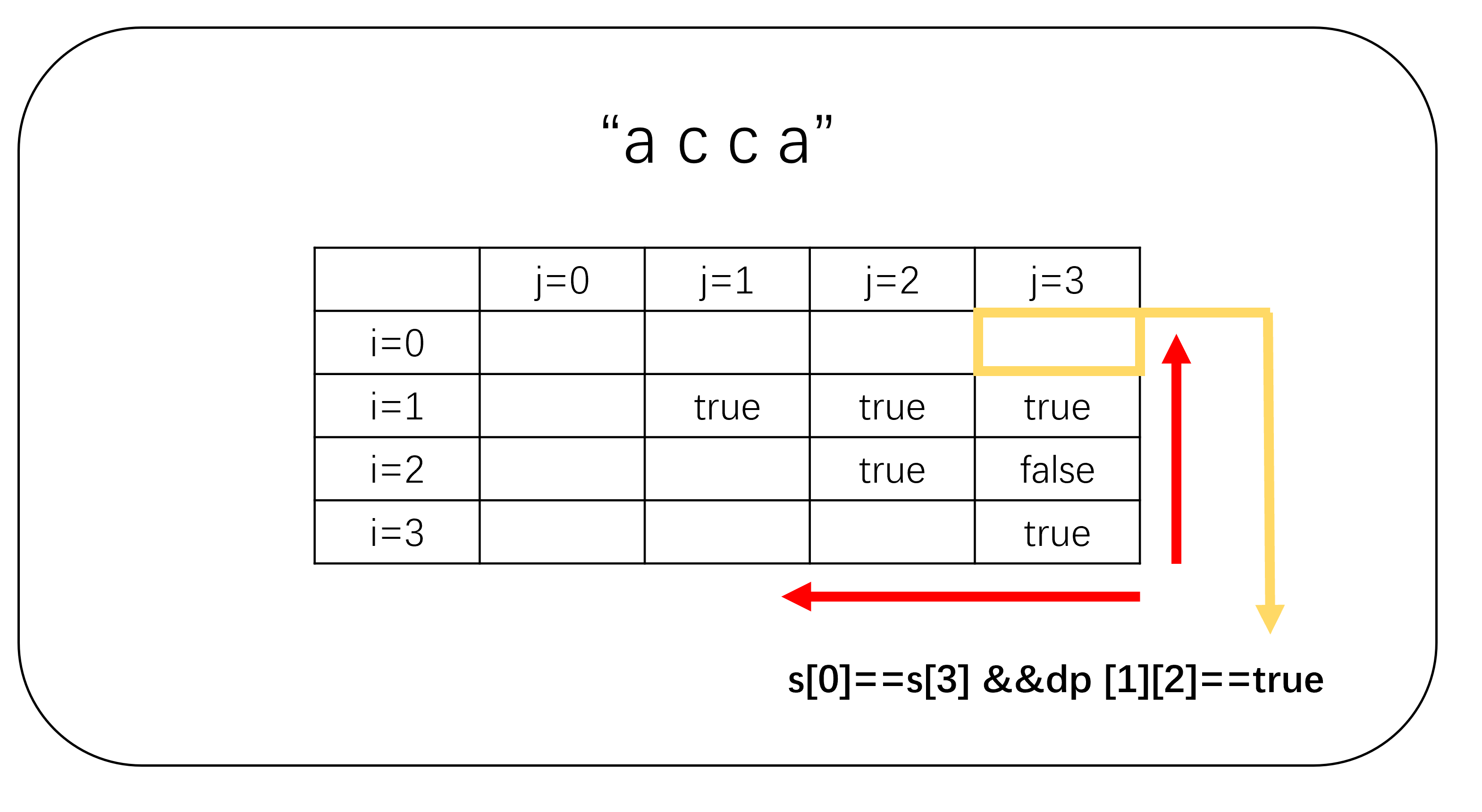
经过上面的分析之后,我们可以得到该算法的代码实现
class Solution {
public:
int countSubstrings(string s) {
int n = s.length();
vector<vector<bool>>dp(n, vector<bool>(n));
int ret = 0;
for(int i = n - 1; i >= 0; i--)
for(int j = n - 1 ; j >= i; j--)
{
if(s[i] == s[j])
if(i + 1 == j || i == j || dp[i + 1][j - 1])
dp[i][j] = true;
if(dp[i][j])
ret++;
}
return ret;
}
};
🚆方法3:中心扩展算法
问题分析:若我们以当前字符为中心,向两边扩展。以"abcba"为例,当我们以c为中心时,两侧扩展,b == b,a == a,因此该字符串为回文串。以这种方法可以判断出奇回文串,也就是以一个字符为中心,两侧字符对称。但它并不能判断出偶回文串,例如"abccba"。这时,我们需要以两个字符为中心,再向两侧扩展。
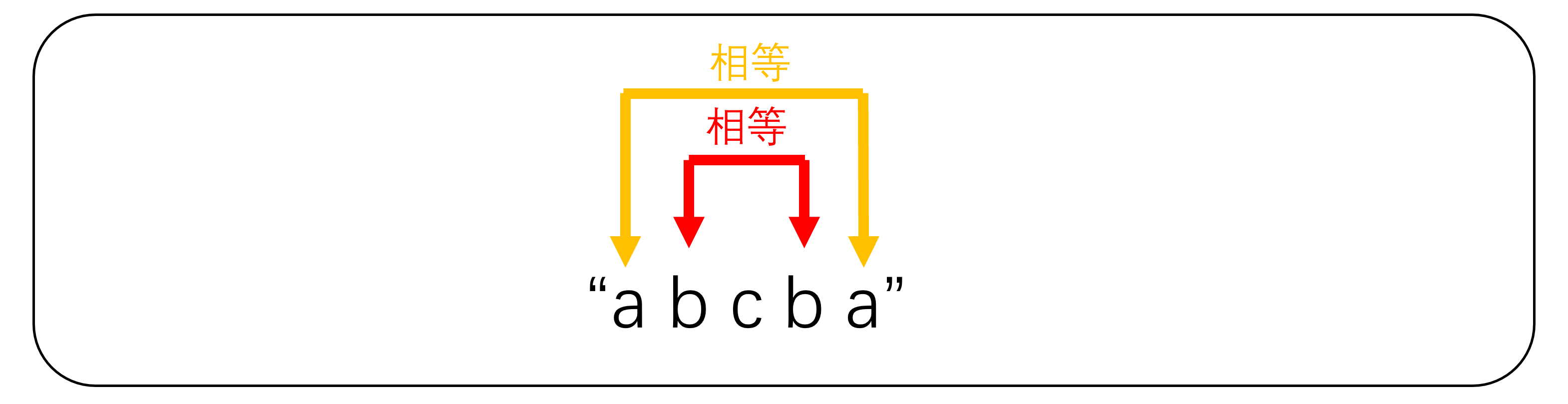
class Solution {
public:
int countSubstrings(string s) {
int n = s.length();
int ret = 0;
for(int i = 0; i < n; i++)
{
//以一个字符扩展
int left = i, right = i;
while(left >= 0 && right <n)
{
if(s[left] == s[right])
ret++;
else
break;
left--;
right++;
}
//以两个字符扩展
if(i == 0 || s[i - 1] != s[i])
continue;
left = i - 1;
right = i;
while(left >= 0 && right < n)
{
if(s[left] == s[right])
ret++;
else
break;
left--;
right++;
}
}
return ret;
}
};
🚆方法4:Manacher马拉车算法
问题分析:马拉车算法是一个比较局限的算法,它仅适用于求最大回文串的问题。若输入字符串的字符总个数为奇数,即奇回文串,此时我们在字符首尾和字符中间添加'#'字符,添加后其仍为奇回文串。若输入的字符串的字符总个数为偶数,即偶回文串,此时我们在字符首尾和字符中间添加'#'字符,添加后其将变为奇回文串。(如下图所示)
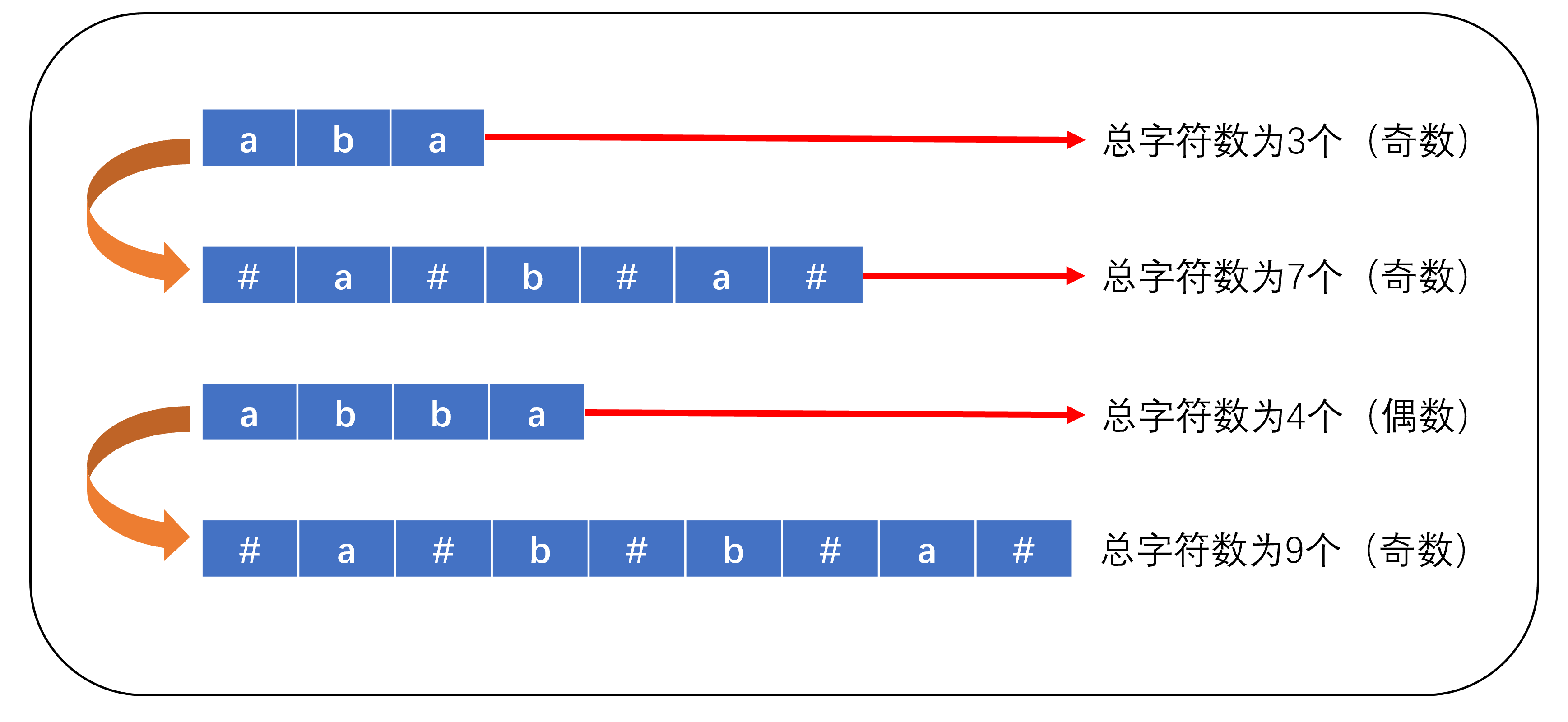
上面的操作是将奇回文串和偶回文串均转换为奇回文串。这是马拉车算法的奇妙之处,为什么这么处理呢?理解完整个算法也许你就知道了。下一步,我们来认识一个概念——回文半径。以"abcba"为例,其回文半径为"abc"或"cba",长度为3。此时我们可以发现:会问半径的长度就等于以c为中心向两侧扩展的回文子串个数。
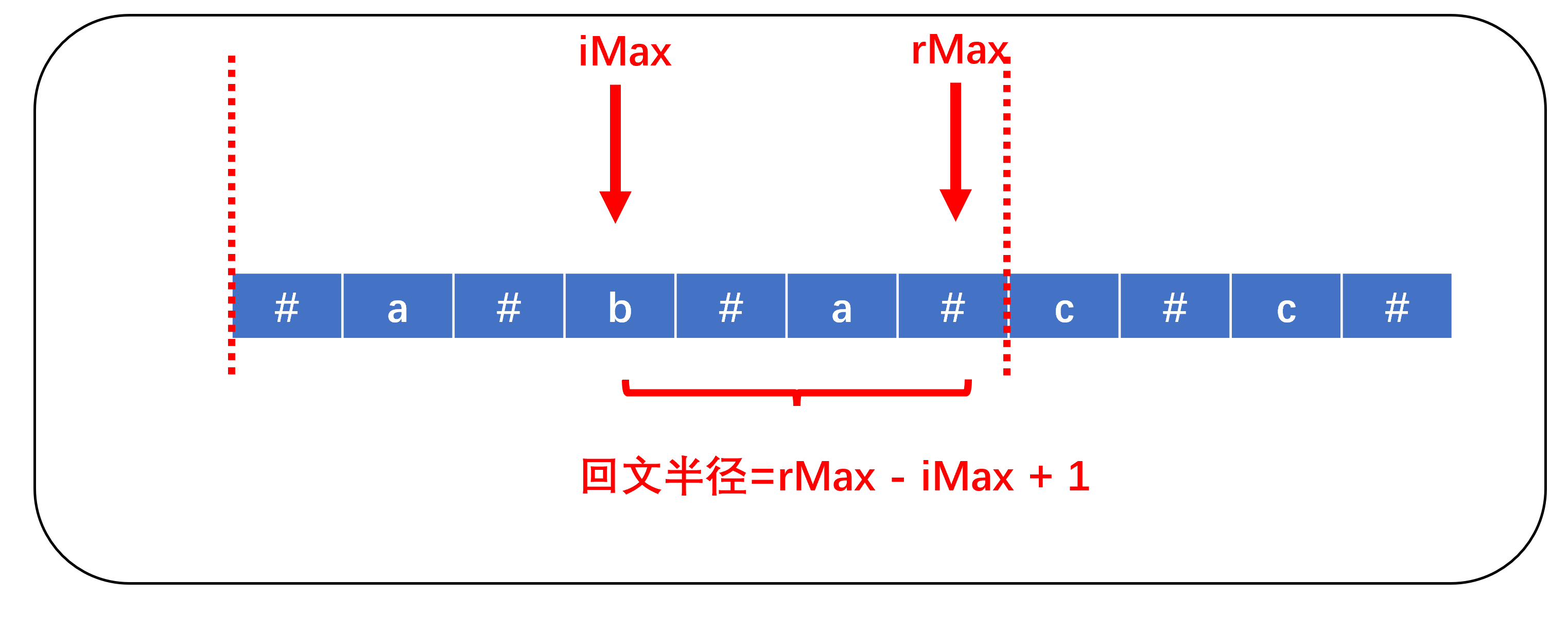
接下来,我们再来理解一个新概念——加速盒子。假如我们知道以下标为iMax的字符串为中心,rMax为iMax +回文半径-1,在我们遍历在计算i = iMax+1的回文半径时,若i<=rMax,则其回文半径为min(d[2 * iMax - i], rMax - i + 1)。这是为什么呢?
已知:iMax为回文串的中心点,rMax = iMax + 回文半径 - 1,回文半径 = rMax - iMax + 1。
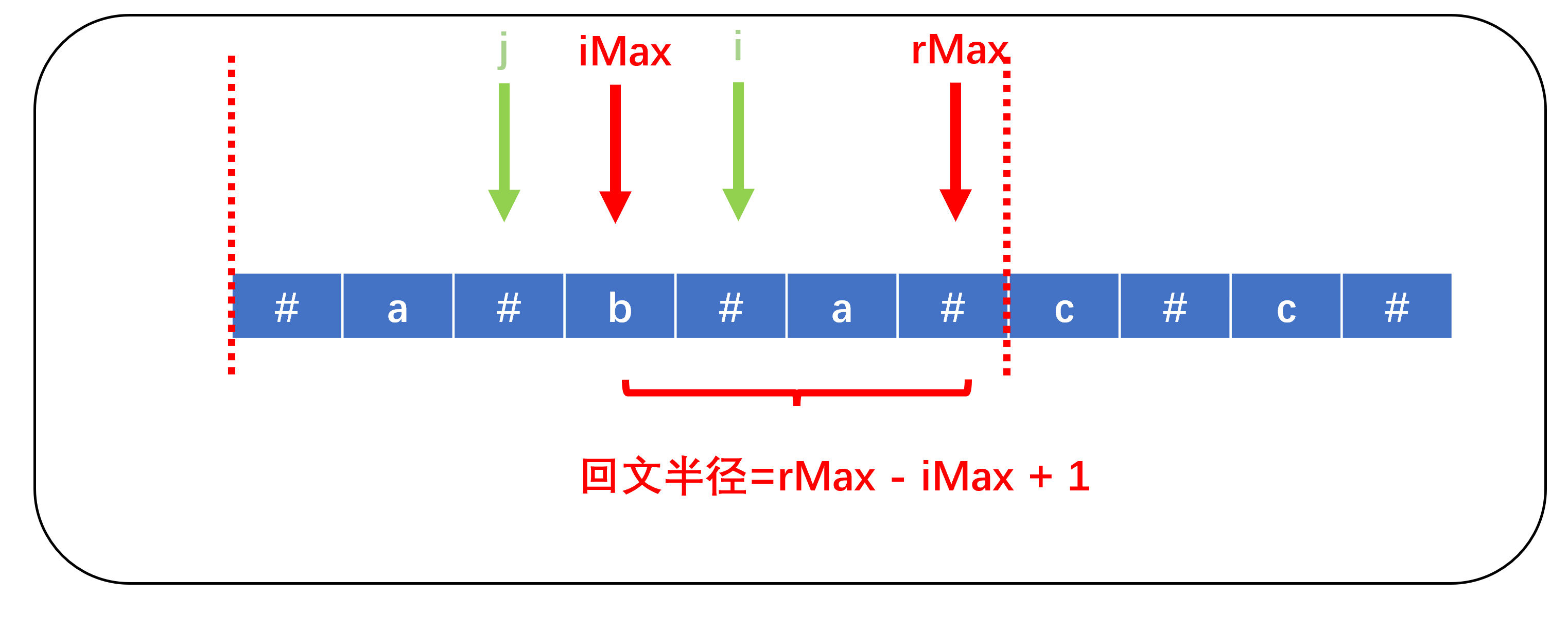
设i=iMax+1,则以iMax为中心的对称点j=iMax - (rMax - iMax + 1 - (rMax - i + 1) ) = 2 * iMax - i。
ps:rMax-iMax+1为回文半径,rMax-iMax+1-(rMax-i+1)为i到iMax的距离
因为我们在求解回文串时都是从左往右遍历,因此i的对称点j的回文半径一定比i先知道,由于i与j对称因此,i和j的回文半径可能相等。但若j的回文半径大于rMax-i+1,也就是j的回文半径超出加速盒子,此时盒子右侧边界之外的字符是未知的,因此我们取rMax-i+1为回文半径。取完这个回文半径并不是最大的回文半径,我们需要使用中心扩展算法继续向两侧扩展,直到两侧字符不相等才终止。同时,若此时i+d[i]-1大于rMax,我们就需要更新加速盒子。
class Solution {
public:
int countSubstrings(string s) {
int n = s.length();
string ms = "$#";
for(int i = 0; i < n; i++)
{
ms += s[i];
ms += '#';
}
ms += '!';
n = ms.length();
vector<int>d(n);
int iMax = 1, rMax = 1, ans = 0;
for(int i = 2; i < n; i++)
{
d[i] = (i <= rMax) ? min(rMax - i + 1, d[2 * iMax - i]) : 1;
while(ms[i - d[i]] == ms[i + d[i]]) ++d[i];
if(i + d[i] - 1 < rMax)
{
iMax = i;
rMax = i + d[i] - 1;
}
ans += d[i] / 2;
}
return ans;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号