LeetCode-1143.最长公共子序列

1143.最长公共子序列

标签：字符串、动态规划

---

题目

🚗问题描述

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

• 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

🚗问题示例

示例 1：

输入：text1 = "abcde", text2 = "ace"
输出：3
解释：最长公共子序列是 "ace" ，它的长度为 3 。

示例 2：
输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。

示例3：

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。

🚗提示

1 <= text1.length, text2.length <= 1000

text1 和 text2 仅由小写英文字符组成。

---

题解

🚆方法1：动态规划

问题分析：面对动态规划，我们可以分为 ①确定状态表示②状态转移方程③初始化④填表顺序⑤返回值 这5个步骤。这道题需要一定的经验，第一次见到比较不容易找到思路。

Step1：确定状态表示->我们以dp[i][j]表示text1[0,i]和text2[0,j]时的最长子序列。

Step2：状态转移方程->我们以text1[0,i]和text2[0,j]最后一个字符为判断条件，若text1[i] == text2[j]，则最长子序列一定包含text[i]和text[j]两个字符。

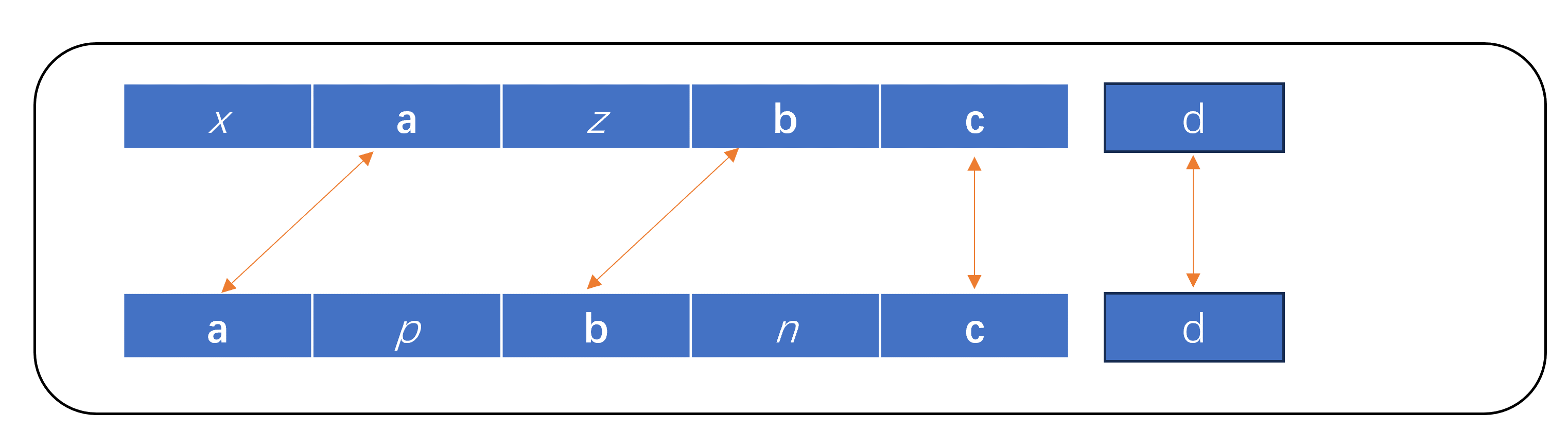
ps：为什么一定包含呢？假定text1[0,i]和text2[0,j]中，两个子串最后一个字符均为"d"；除text1[i]及text2[j]外，已知最长子序列为abc，长度为3，即text1[0,i-1]和text2[0,j-1]的最长子序列为3。那么text1[0,i]和text2[0,j]的最长子序列必定为4。（如下图所示）

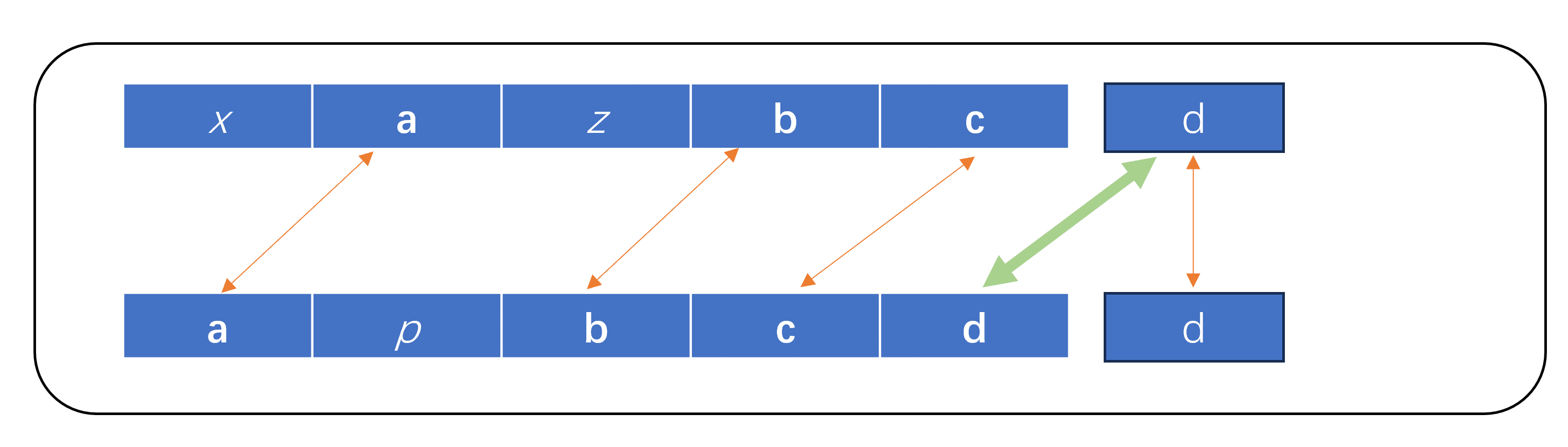
ps：假定出现下图这种情况，又应该如何处理呢？其实，我们认定绿色箭头所指向的两个"d"相等 和 认定橙色箭头指向的两个"d"相等得到的最长子序列的大小是一样的，并不影响结果。为了和上面的一般情况合并处理，我们这里认定橙色箭头两个"d"为最长子序列的最后一个字符。

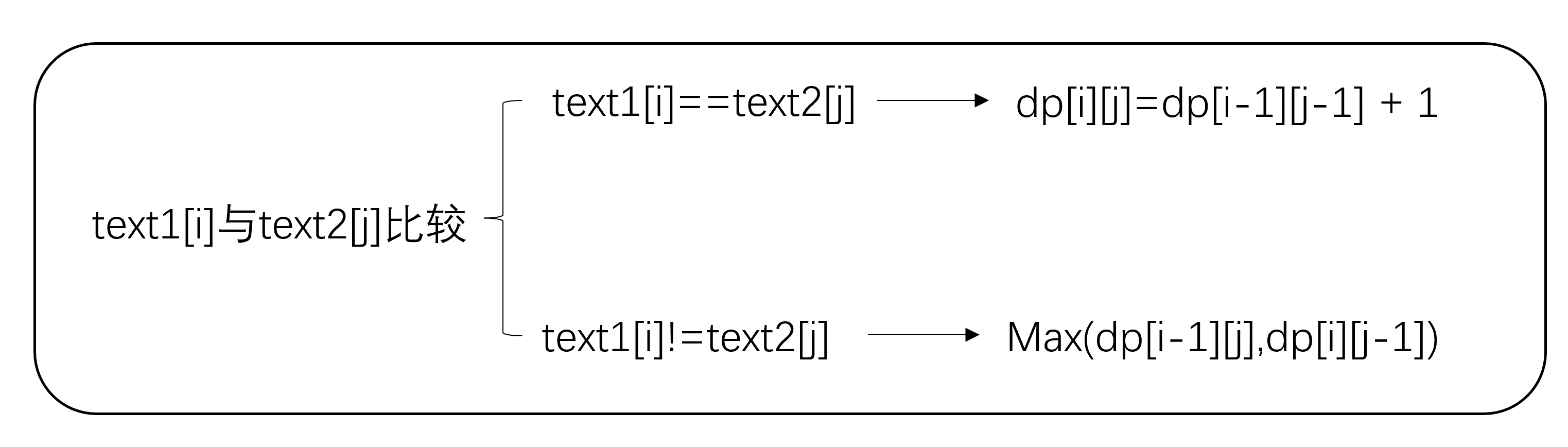
经过上面的分析后，我们可以得到如下的状态转移方程：若text1[i]==text2[j]，则dp[i][j]=dp[i-1][j-1]+1；若text1[i]!=text2[j]，则dp[i][j]=max(dp[i-1][j],dp[i][j-1])。

Step3：初始化->二维dp表每个元素初始应该为0，因为极端情况下，可能没有最长公共子序列。另外，为了防止越界，我们可以多开辟一行一列，从而text1[0]或text2[0]均表示空串，因而第0行与第0列应初始化为0。

Step4：填表顺序->因为dp[i][j]依赖于dp[i-1][j-1]、dp[i][j-1]、dp[i-1][j]，即依赖于左上元素、左侧元素和上侧元素，因此填表顺序应从左上自右下。

Step5：返回值->由上面分析可以得到返回值应为dp[text1.length()][text2.length()]。

经过上面的分析整理得到如下代码：

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m = text1.length();
        int n = text2.length();
		vector<vector<int>>dp(m + 1, vector<int>(n + 1));
        for(int i = 1; i <= m; i++)
            for(int j = 1; j <= n; j++)
                if(text1[i - 1] == text2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
		return dp[m][n];
    }
};