11.13

简述在决策树算法中，以信息增益和信息率为属性划分标准的问题分别是什么？

我的答案：

 

1. 信息增益作为属性划分标准的问题

   偏向选择取值较多的属性：        信息增益的计算方式会导致决策树算法更倾向于选择那些具有较多取值的属性。例如，在一个包含客户信息（如姓名、年龄、性别、购买记录等）的数据集里，如果有一个属性是客户的唯一识别码（每个客户都不同），这个属性的取值非常多。        根据信息增益的计算，该属性会有很大的信息增益，因为它几乎可以完美地区分每一个样本，从而使数据集的混乱度（熵）迅速降低。但实际上，这个属性对于分类（比如预测客户是否会购买某产品）没有实际意义，这就可能导致过拟合，模型在训练数据上表现很好，但在新数据上效果不佳。    对可取值数目较少的属性不公平**：        对于取值较少的属性，即使它们可能对分类结果有重要意义，在信息增益的评估标准下也可能被忽视。例如在判断水果是苹果还是橙子的简单分类任务中，“颜色”这个属性可能只有“红色”“橙色”等几个取值，但对分类结果非常关键。        然而，当数据集中存在取值更多的无关属性（如水果的条形码编号）时，“颜色”属性的信息增益可能相对较小，导致决策树构建时不能优先选择这个有实际意义的属性。 2. 信息率作为属性划分标准的问题    计算复杂度过高：        信息率的计算涉及到信息增益和分裂信息（split information）。分裂信息用于衡量属性分裂数据的广度和均匀性，其计算需要考虑属性的每个取值的分布情况。        例如，在一个大规模数据集上，若某个属性有大量不同的取值，计算分裂信息需要对每个取值的样本数量进行统计和计算，这会消耗大量的计算资源和时间，导致算法效率降低。    对噪声敏感：        信息率在计算过程中对数据中的噪声较为敏感。当数据存在噪声（如错误的分类标签或不准确的属性值）时，会影响分裂信息的计算。        假设在一个医疗诊断数据集中，部分患者的诊断结果被误标记，在计算属性的信息率时，可能会使一些原本有价值的属性被错误地评估，进而影响决策树的构建，降低决策树的准确性和稳定性。 信息增益和信息率在决策树算法的属性划分中都有各自的优缺点，在实际应用中需要根据具体情况进行选择或改进。

2. (简答题)在决策树算法中，预剪枝和后剪枝的优劣？

我的答案：

 

预剪枝 优点    计算效率高：预剪枝在决策树构建过程中提前停止生长，避免了对大量不必要分支的生成和计算。例如，在一个大型数据集上构建决策树，如果采用预剪枝，当树生长到一定深度或节点的样本数低于某个阈值时，就不再继续分裂节点。这样可以大大减少计算量，尤其是在处理海量数据时，能显著提高算法的运行速度。    简单有效防止过拟合：通过提前设定的规则，如限制树的深度、设定最小样本数或最小信息增益等阈值，能够直观地控制决策树的复杂度，从而在一定程度上避免生成过于复杂的决策树，有效地防止过拟合。比如，在一个小规模数据集上，如果不进行剪枝，决策树可能会对训练数据中的噪声过度学习，但预剪枝可以在早期就遏制这种趋势。 缺点    可能导致欠拟合：由于预剪枝是基于一些提前设定的规则来决定是否停止树的生长，可能会在决策树还未充分学习到数据中的有效信息时就停止生长。例如，在某些复杂的数据分布情况下，可能存在一些重要的特征需要在较深的层次才能体现出其分类价值，但预剪枝可能因为当前的深度限制而忽略这些特征，导致模型的泛化能力受限，出现欠拟合现象。    需要合理设定阈值：预剪枝的效果很大程度上依赖于所设定的阈值参数，如树的深度阈值、最小样本数阈值等。如果这些阈值设置不合理，可能无法达到预期的剪枝效果。例如，如果树的深度阈值设置过小，可能会导致决策树过于简单，无法捕捉数据中的复杂关系；反之，如果阈值设置过大，预剪枝的作用就会减弱，可能仍然会出现过拟合问题。 后剪枝 优点    通常能获得更好的泛化能力：后剪枝是在决策树完全生长之后进行的，它基于对整个树结构的分析来去除那些对泛化能力没有帮助的子树。这使得决策树在充分学习数据中的信息之后，再进行优化，从而能够保留更多重要的特征和结构，通常能得到比预剪枝更好的泛化能力。例如，在处理一些复杂的非线性数据分类问题时，后剪枝可以在决策树充分生长并学习到数据中的复杂模式后，对不必要的细节进行修剪，使模型在新数据上的表现更好。    不需要过多的提前设定：与预剪枝相比，后剪枝不需要对树的生长过程进行过多的提前干预，不需要精确地设定诸如树的深度、节点样本数等阈值。后剪枝更多地是基于对已生成树的评估，如使用验证集数据来判断子树是否应该被剪掉，这种方式更加灵活，对不同类型的数据和问题具有更好的适应性。 缺点    计算成本高：后剪枝需要先构建完整的决策树，这本身就需要大量的计算资源和时间，然后还要对已生成的树进行回溯和修剪，对每个非叶子节点都要考虑是否剪枝以及剪枝后的效果评估。例如，在处理大数据集或具有大量特征的数据集时，构建完整的决策树可能会消耗大量的内存，而后剪枝过程中的反复评估和计算会进一步加重计算负担，导致算法效率低下。    可能存在过拟合风险：尽管后剪枝的目的是防止过拟合，但在某些情况下，如果剪枝策略不当，例如在评估子树是否剪枝时使用的验证集数据本身存在偏差或噪声，可能会导致错误的剪枝决策，从而使模型仍然保留一些过拟合的特征，无法达到最佳的泛化效果。 预剪枝和后剪枝在不同的应用场景和数据条件下各有优劣，在实际使用决策树算法时，需要根据具体情况合理选择剪枝策略。

3. (简答题)在决策树算法中，三个算法终止条件分别是？

我的答案：

 

1. 节点中所有样本属于同一类别

2. 没有剩余属性可供划分

3. 样本数量小于某个阈值

二. 计算题（共1题，25分）

4. (计算题)

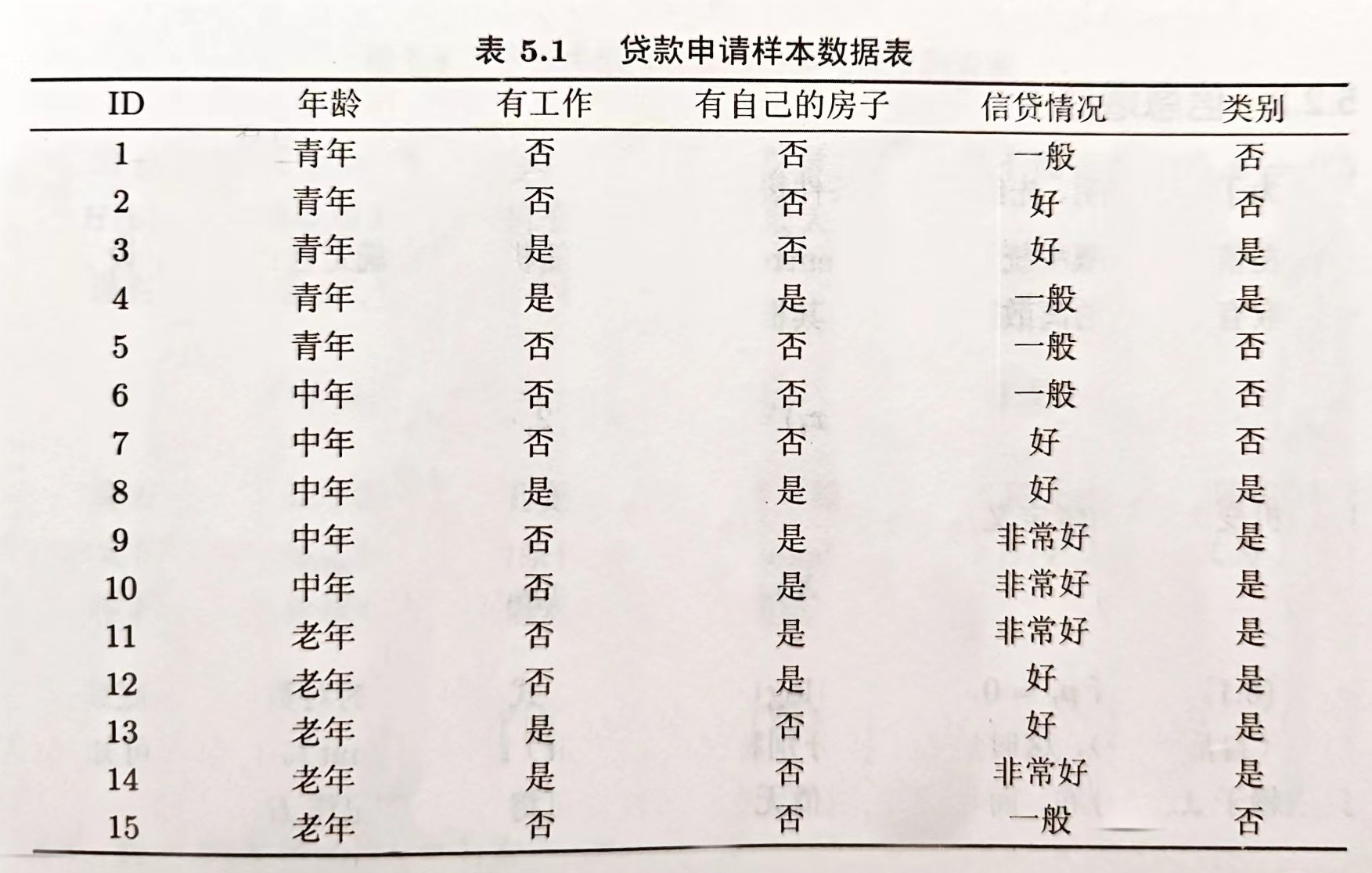
对上表中的数据，利用ID3算法（以信息增益为属性划分标准）建立决策树。

我的答案：

 

1. 计算初始信息熵：

   首先统计类别情况，在给定的数据中，类别情况并不明确，假设这里需要我们自己根据已有信息判断类别。如果假设类别只有两类，比如“可贷款”和“不可贷款”，需要先观察数据中哪些特征可能与贷款相关，比如信贷情况。    假设信贷情况为“好”或“非常好”的可以初步判断为“可贷款”，其他情况为“不可贷款”。这样统计可得，“可贷款”的数量假设为 n1，“不可贷款”的数量为 n2。   总样本数为 n = n1 + n2。   初始信息熵计算公式为：Entropy(S)=−p+×log2(p+)−p−×log2(p−)，其中 p+ = n1/n，p− = n2/n。 2. 计算各属性的信息增益：    年龄属性：分为青年、中年、老年三类。分别统计每类中“可贷款”和“不可贷款”的数量，计算出每类的信息熵，再根据每类样本占总样本的比例加权求和，得到该属性的条件熵。信息增益 = 初始信息熵 - 条件熵。    有工作属性：由于数据中该属性大多缺失，暂不考虑该属性计算信息增益。    有自己的房子属性：同样因为数据中该属性大多缺失，暂不考虑。    信贷情况属性：分为一般、好、非常好等情况，分别统计每种情况中“可贷款”和“不可贷款”的数量，计算条件熵，进而得到信息增益。 3. 选择信息增益最大的属性作为根节点进行划分：    比较年龄、信贷情况等属性的信息增益，选择信息增益最大的属性作为决策树的根节点。假设信贷情况属性的信息增益最大，则以信贷情况作为根节点进行划分。 4. 对划分后的子节点重复上述步骤：   对于信贷情况为“好”和“非常好”的子节点，继续计算其他属性（如年龄等）的信息增益，选择信息增益最大的属性进行进一步划分。对于信贷情况为“一般”的子节点也进行同样的操作。 5. 重复步骤直到满足决策树停止生长的条件：   当节点中的样本全部属于同一类别，或者没有剩余属性可供划分，或者样本数量小于某个阈值时，停止生长决策树。