XMOJ 2025-4

A：二叉树的路径

观察发现，如果一个节点的下标为 \(x\)，则左儿子对应的下标永远为 \(2x+1\)，右儿子则为 \(2x+2\)

于是可以简单粗暴使用搜索维护 path 数组记录每个点的路径

实现很简单

B：铺硬币游戏

通过手模，可以得出一个必胜方法

先发者为红

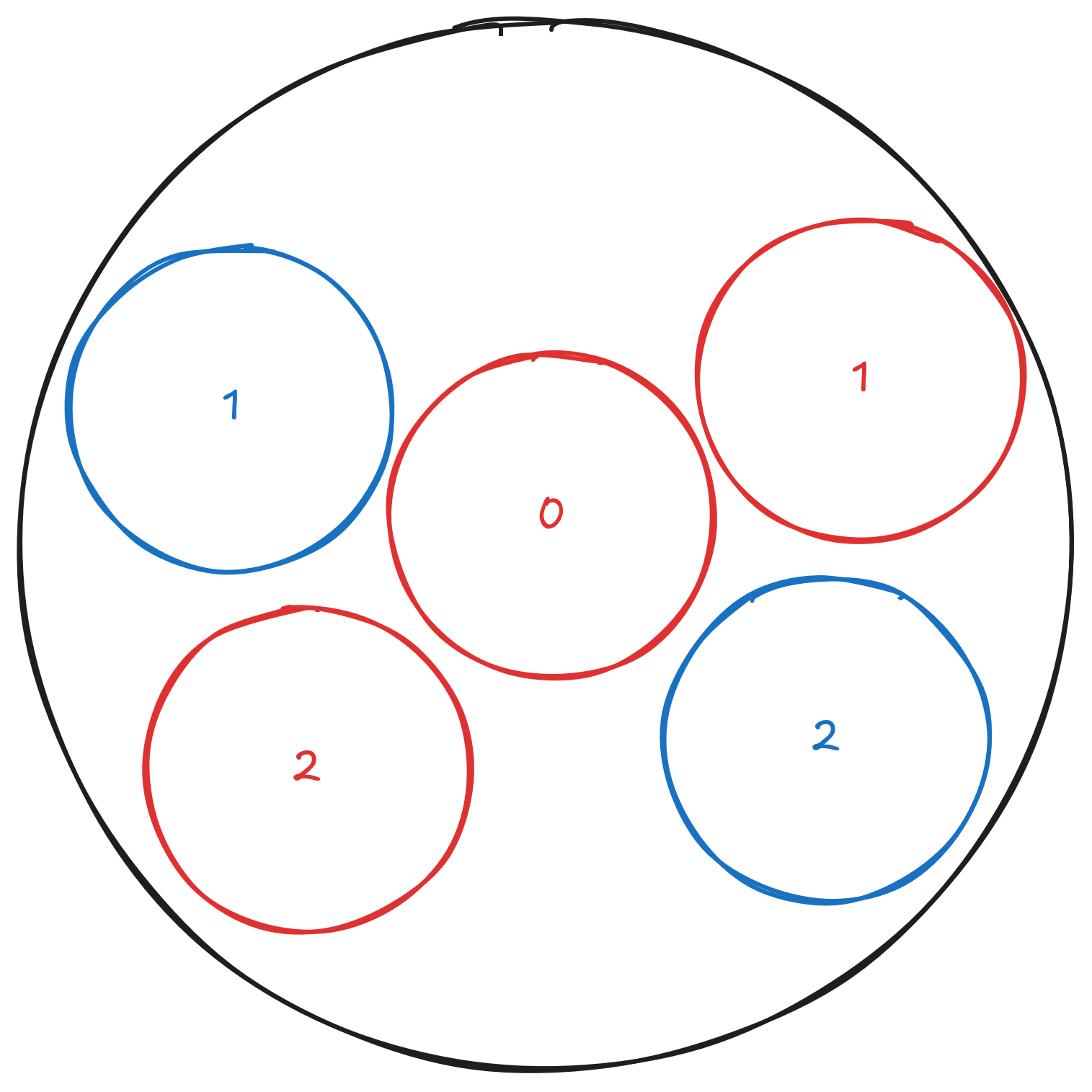
如图，第一步先铺到圆心，之后每一步都与对手对称，根据三角形的基本性质，对手能走你就能走，于是对手必输

但还有一个特殊情况，就是第一步都放不下，只需判断这一种情况即可

实现很简单

C：台词

模拟题，不说了，直接贴代码：

#include <bits/stdc++.h>
#define int long long
#define WORONG                \
    cout << "WRONG!" << endl; \
    return;
#define CORRECT                        \
    cout << "CORRECT (maybe)" << endl; \
    return;
const int N = 1e5 + 5;
const int Mod = 1e9 + 7;
using namespace std;
string S;
void solve()
{
    string name = "";
    int i = 0;
    while (i < S.size() && S[i] != ' ')
    {
        name += S[i];
        i++;
    }
    if (i + 1 >= S.size())
    {
        WORONG
    }
    S = S.substr(i + 1);
    if (S.empty())
    {
        WORONG
    }
    if (name == "rabi")
    {
        for (char i : S)
        {
            if (isalnum(i))
            {
                CORRECT
            }
        }
        WORONG
    }
    i = S.size() - 1;
    while (i >= 0 && !isalnum(S[i]))
    {
        if (S.size() - i > 3)
        {
            WORONG
        }
        i--;
    }
    cerr << S << endl;
    S = S.substr(0, i + 1);
    cerr << S << endl;
    if (name == "digi" || name == "petit" || name == "piyo")
    {
        if (S.size() < 3)
        {
            WORONG
        }
        string tmp;
        for (int i = S.size() - 3; i < S.size(); i++)
        {
            tmp += tolower(S[i]);
        }
        if (name == "digi" && tmp == "nyo")
        {
            CORRECT
        }
        if (name == "petit" && tmp == "nyu")
        {
            CORRECT
        }
        if (name == "piyo" && tmp == "pyo")
        {
            CORRECT
        }
    }
    if (name == "gema")
    {
        if (S.size() < 4)
        {
            cout << "WRONG!" << endl;
            return;
        }
        string tmp;
        for (int i = S.size() - 4; i < S.size(); i++)
        {
            tmp += tolower(S[i]);
        }
        if (tmp == "gema")
        {
            CORRECT
        }
    }
    WORONG
}
signed main()
{
    freopen("dialogue.in", "r", stdin);
    freopen("dialogue.out", "w", stdout);
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    while (getline(cin, S))
    {
        solve();
    }
    return 0;
}

注意点：一定要搞清 STL 函数的意义，不然就调半天都调不出来

D：最长倍数序列

先进行排序

设 \(dp_x\) 为结尾为 \(x\) 的情况下最长倍数序列的长度

枚举 \(x\) 的因数，\(dp_x\) 可以由它们转移过来

取最大即可，别忘了加 \(1\)

E：红绿蓝涂色

开始上难度了

因为涂色最多连续涂两个

把涂出来的色块分为两部分，一个组和两个组

• 遍历两个组数量 \(two\)，便可得知一个组数量 \(one\)

  • 把最少使用的格子数量超过 \(n\) 的判掉

  • 遍历两个组中有红色的数量 \(r\)

    • 把剩余蓝绿组合无法填满的判掉
    • 计算剩余空白个数
    • 
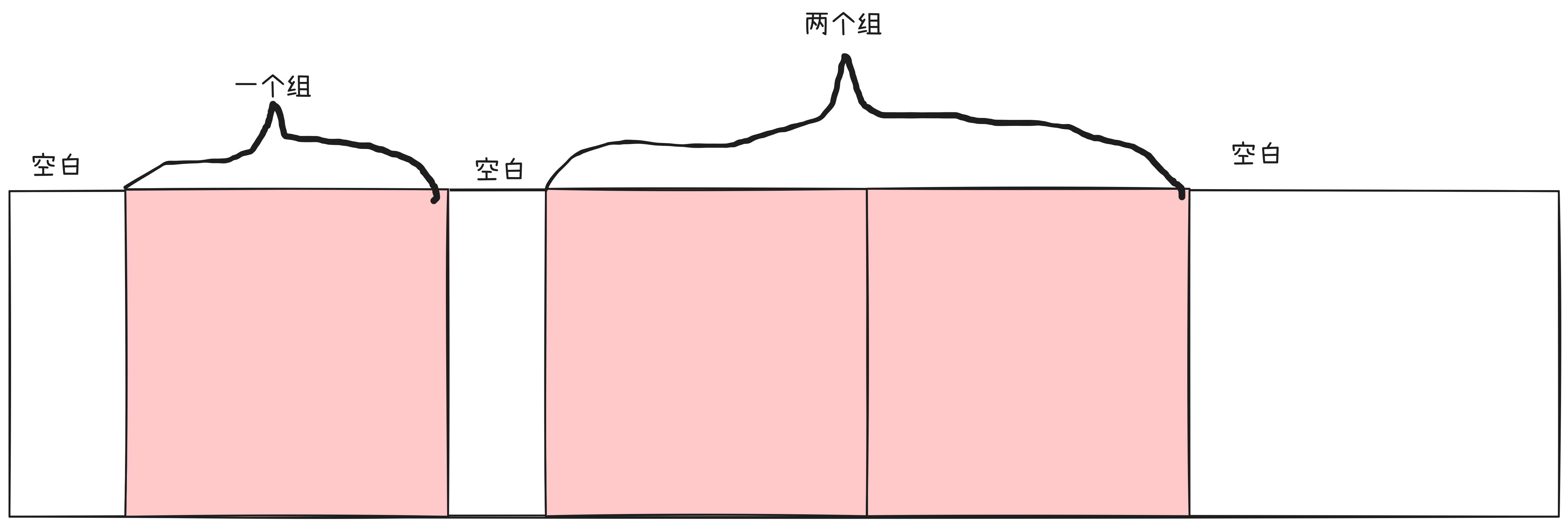
      由图片可知，组之间的空白数量为 \(two + one - 1\)，每个空白至少有一个格子。而两边的空白数量为 \(2\)，至少有 \(0\) 个格子
    • 使用栅栏法求出空白位置可能性，再乘上用组合数求出的一二组别位置可能性以及两个组前后交换可能性，即可得知位置可能性 \(placeCnt\)
    • 接着，将利用组合数算出的把红色分给两个组的可能性乘上把剩下的红色分给一个组的可能性，即可知道红色分配可能性 \(redCnt\)
    • 最后，再用组合数求出绿色可能性 \(greenCnt\)
    • 三个数相乘就是答案

记得取模

F：喜欢蓝宝石

一眼二分答案，因为符合单调性

然后由于是环，所以要先“破环成链”

现在思考 check 函数的写法

我们可以发现，蓝色在 \(\left[l,r\right]\) 区间占比为区间总和除以区间总数，所以要满足的式子就是：

\[\frac{\sum_{i=l}^{r} a_i}{r - l + 1} \geq mid \]

我们可以先移项，得：

\[\sum_{i=l}^{r} a_i \geq mid(r - l + 1) \]

再移项，得：

\[\sum_{i=l}^{r} a_i - mid(r - l + 1) \geq 0 \]

可以发现，减去的式子就相当于每项都减去 \(mid\)

所以，我们可以先将每一项都减去 \(mid\)，再求前缀和

答案的判断就是判断是否有 \(sum_r \geq sum_l\) 在 \(l < r\) 并且 \(k \leq r - l \leq n\) 的情况下

于是我们可以先确定 \(l\)，之后再在 \(\left[l + x, l + n\right]\) 中找一个 \(sum\) 的最大值与 \(sum_l\) 相减判断差是否大于等于 \(0\);

使用滑动窗口维护即可

记得用双精度浮点数