Floyd算法【最短路1】

Floyd算法是最短路问题的入门算法，后期有和他类似的Dijkstra算法(迪杰斯特拉，简称dij算法)，Floyd算法的时间复杂度是O(n³)，即三个for循环，适合数据量小的题目，但是这似乎很少用到，大多数情况下仍是使用dij算法，但作为最短路问题的初级算法，他比dij容易理解得多。

核心思路：

通过下面的例题，详细解答，

 

 

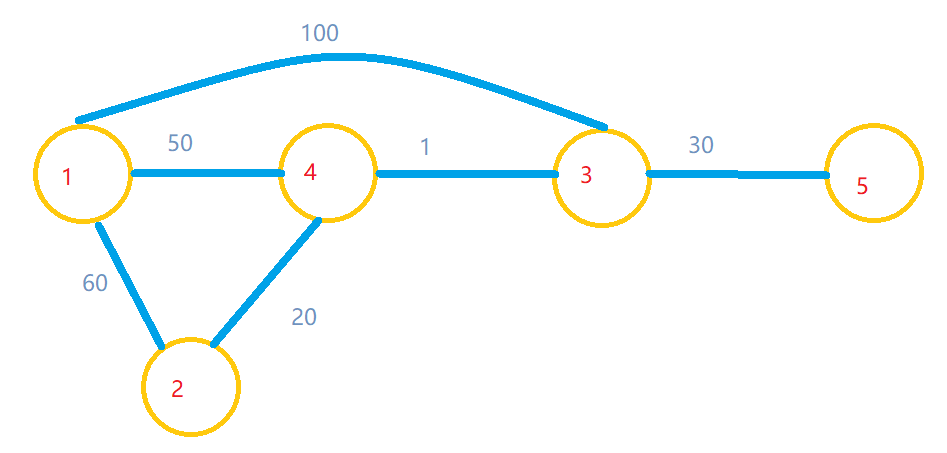
 从1号点出发，5号点结束，求找到一条最短的路径，当然你可以一眼看出1-4-3-5是最短的，但是作为程序，你需要从1号点出发，遍历每一条边的权值(这是Floyd算法的重点也是一句废话)，即第一层循环就是每个中转站的点(问题来了，中转站的点是否可以包含起点和终点呢？)，第二层循环表示的是起点，第三层循环指的是终点，通过判断是直接从起点到终点直接的路径短呢？还是通过中转站的路径短？如果直接路径更短的话，那就忽略吧，否则将简介路径的值赋值给直接(最终，默认直接路径是最短的路径)路径。刚才的问题已经解答完毕，假设中转站是起点或者是终点，那么起点到中转站的距离或者是中转站到终点的距离即为0，无意义，直接忽略。

注意：这边存在一种特殊情况默认的情况下都是直接走的，不经过中转站，如上图，1-3的直接路径是100个单位，而1-4-3的间接路径相比1-3的直接路径会短的很多，所以要把所有边的路径都给跑个遍。

基础模板

注意：for循环的顺序不可以改变不然就wa

for(ll k=1;k<=节点数;k++)
    {
        for(ll i=1;i<=节点数;i++)
        {
            for(ll j=1;j<=节点数;j++)
            {
                if(a[i][k]+a[k][j]<a[i][j])
                {
                    a[i][j]=a[i][k]+a[k][j];
                }
            }
        }
    }

参考题目：

P2910 [USACO08OPEN]Clear And Present Danger S

题目意思指的是，你要从1号岛到n号岛，给出一个n*n规模大小的危险值表(不一定是对称矩阵，也就是说危险值_a-b ≠ 危险值_b-a)，要求你寻找出从1号岛到n号岛危险值最小的一个值，由于是入门题，不要求输出具体的最短路径

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m;
ll a[105][105],s,d[100005];
int main()
{
    scanf("%lld%lld",&n,&m);
    for(ll i=1;i<=m;i++)
    {
        scanf("%lld",&d[i]);
    }
    for(ll i=1;i<=n;i++)
    {
        for(ll j=1;j<=n;j++)
        {
            scanf("%lld",&a[i][j]);
        }
    }
    for(ll k=1;k<=n;k++)
    {
        for(ll i=1;i<=n;i++)
        {
            for(ll j=1;j<=n;j++)
            {
                if(a[i][k]+a[k][j]<a[i][j])
                {
                    a[i][j]=a[i][k]+a[k][j];
                }
            }
        }
    }
    for(ll i=2;i<=m;i++)
    {
        s+=a[d[i-1]][d[i]];
    }
    printf("%lld\n",s);;
}

 

在带权有向图G中，求G中的任意一对顶点间的最短路径问题，也是十分常见的一种问题。

解决这个问题的一个方法是执行n次迪杰斯特拉算法，这样就可以求出每一对顶点间的最短路径，执行的时间复杂度为O(n³)。

而另一种算法是由弗洛伊德提出的，时间复杂度同样是O(n3)，但算法的形式简单很多。

可以将弗洛伊德算法描述如下：

在本题中，读入一个有向图的带权邻接矩阵（即数组表示），建立有向图并按照以上描述中的算法求出每一对顶点间的最短路径长度。

输入

输入的第一行包含1个正整数n，表示图中共有n个顶点。其中n不超过50。

以后的n行中每行有n个用空格隔开的整数。对于第i行的第j个整数，如果大于0，则表示第i个顶点有指向第j个顶点的有向边，且权值为对应的整数值；如果这个整数为0，则表示没有i指向j的有向边。当i和j相等的时候，保证对应的整数为0。

输出

共有n行，每行有n个整数，表示源点至每一个顶点的最短路径长度。如果不存在从源点至相应顶点的路径，输出-1。对于某个顶点到其本身的最短路径长度，输出0。

请在每个整数后输出一个空格，并请注意行尾输出换行。

样例输入 Copy

4
0 3 0 1
0 0 4 0
2 0 0 0
0 0 1 0

样例输出 Copy

0 3 2 1 
6 0 4 7 
2 5 0 3 
3 6 1 0 

提示

在本题中，需要按照题目描述中的算法完成弗洛伊德算法，并在计算最短路径的过程中将每个顶点是否可达记录下来，直到求出每一对顶点的最短路径之后，算法才能够结束。

相对于迪杰斯特拉算法，弗洛伊德算法的形式更为简单。通过一个三重循环，弗洛伊德算法可以方便的求出每一对顶点间的最短距离。

另外需要注意的是，为了更方便的表示顶点间的不可达状态，可以使用一个十分大的值作为标记。而在题目描述中的算法示例使用了另外一个三维数组对其进行表示，这使原本的O(n³)时间复杂度增长到了O(n⁴)，这也是需要自行修改的部分。

 

相较网上其他做法而言，大多数都是采用fill去初始化a数组的，查过资料，memset比fill的处理速度会更快一些

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f;
ll n;
ll a[55][55];
int main()
{
    memset(a,inf,sizeof a);//初始化a数组最大
    scanf("%lld",&n);
    for(ll i=1;i<=n;i++)
    {
        for(ll j=1;j<=n;j++)
        {
            scanf("%lld",&a[i][j]);
            if(a[i][j]==0&&i!=j)//表示i到j不能够到达，默认为inf最大
            {
                a[i][j]=inf;
            }
        }
    }
    for(ll k=1;k<=n;k++)
    {
        for(ll i=1;i<=n;i++)
        {
            for(ll j=1;j<=n;j++)
            {
                if(a[i][j]>a[i][k]+a[k][j]&&a[i][k]!=inf&&a[k][j]!=inf)//如果i到k和k到j能够走得通，则表示i到j也一定可以走通，包括间接路径和直接路径
                {
                    a[i][j]=a[i][k]+a[k][j];
                }
            }
        }
    }
    for(ll i=1;i<=n;i++)
    {
        for(ll j=1;j<=n;j++)
        {
            if(j!=1)
            {
                printf(" ");
            }
            if(a[i][j]==inf)//将之前i到j走不通的inf设为-1
            {
                a[i][j]=-1;
            }
            printf("%lld",a[i][j]);
        }
        printf("\n");
    }
}