蚁群算法（ACA)及其Matlab实现

1基本原理：

本质上也是一种概率算法，通过大概率收敛到最佳值，和其他的智能算法很相似。蚁群分泌的信息素存在正反馈，使得较佳的解

具有大概率被选到，当全局都选用较佳的解，变可以得到整体的最优解。

2几个关键点：

  1） 概率选择：

      受信息素浓度和启发函数影响，启发函数为距离的倒数

   2）信息素挥发

      考虑到信息素随时间的挥发，加入挥发因子                

3程序设计步骤：

    1初始化各个参数：包括各点的距离，信息素的初始浓度，蚂蚁数量，信息素挥发因子，

                                    信息素和启发函数的重要度因子，启发函数，最大迭代次数，路径记录表等等

      2迭代：对每个蚂蚁随机制定初始值，再根据概率选择，选择出每只蚂蚁的路径，确定每只蚂蚁的路径总长度，

                   以及蚁群的最佳路径长度和平均长度，并对信息素进行更新。

      3展示：展示出最佳路径，以及最佳路径对迭代的变化图

   4Matlab代码

 

clc,clear                                                                                    %清空环境中的变量
load data.txt                                                                           %读入城市的坐标
t0 = clock;                                                                                %程序计时开始
%%
%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%
city=data;
n = size(city,1);                                                                      %城市距离初始化
D = zeros(n,n);                                                    
for i = 1:n
    for j = 1:n
           if i ~= j
            D(i,j) = sqrt(sum((city(i,:) - city(j,:)).^2));
        else
            D(i,j) = 0;      %设定的对角矩阵修正值
        end
    end    
end
m=30;                                                                                        %蚂蚁数量
alpha = 1;                                                                                 % 信息素重要程度因子
beta = 5;                                                                                  % 启发函数重要程度因子
v = 0.1;                                                                                     % 信息素挥发因子
Q = 0.5;                                                                                     % 信息因子常系数
H= 1./D;                                                                         % 启发函数
T= ones(n,n);                                                                         % 信息素矩阵
Table = zeros(m,n);                                                               % 路径记录表
iter = 1;                                                                                    % 迭代次数初值
iter_max = 50;                                                                     % 最大迭代次数 
best_route = zeros(iter_max,n);                                       % 各代最佳路径       
best_length = zeros(iter_max,1);                                     % 各代最佳路径的长度  
%%
while iter<=iter_max
   
                        % 随机产生每只蚂蚁的起点城市
                          start = zeros(m,1);
                          for i = 1:m
                              temp = randperm(n);
                              start(i) = temp(1);
                          end
                          Table(:,1) = start; 
                          city_index=1:n;
                          for i = 1:m
                          % 逐个城市路径选择
                         for j = 2:n
                             tabu = Table(i,1:(j - 1));                                                   % 已访问的城市集合
                             allow =city_index( ~ismember(city_index,tabu));    % 筛选出未访问的城市集合
                             P = zeros(1,length(allow));
                             % 计算相连城市的转移概率
                             for k = 1:length(allow)
                                 P(k) = T(tabu(end),allow(k))^alpha * H(tabu(end),allow(k))^beta;
                             end
                             P = P/sum(P);
                             % 轮盘赌法选择下一个访问城市
                            Pc = cumsum(P);     %参加说明2(程序底部)
                            target_index = find(Pc >= rand); 
                            target = allow(target_index(1));
                            Table(i,j) = target;
                         end
                      end

                          % 计算各个蚂蚁的路径距离
                                  Length = zeros(m,1);
                                  for i = 1:m
                                      Route = [Table(i,:) Table(i,1)];
                                      for j = 1:n
                                          Length(i) = Length(i) + D(Route(j),Route(j + 1));
                                      end
                                  end   
             %对最优路线和距离更新            
                   if iter == 1
                      [min_length,min_index] = min(Length);
                      best_length(iter) = min_length;  
                      best_route(iter,:) = Table(min_index,:);
                  else
                      [min_length,min_index] = min(Length);
                           if min_length<best_length(iter-1)
                                     best_length(iter)=min_length;
                                     best_route(iter,:)=Table(min_index,:);
                           else
                                    best_length(iter)=best_length(iter-1);
                                    best_route(iter,:)=best_route(iter-1,:);
                           end 
                   end
                            % 更新信息素
                          Delta_T= zeros(n,n);
                          % 逐个蚂蚁计算
                          for i = 1:m
                              % 逐个城市计算
                              Route = [Table(i,:) Table(i,1)];
                              for j = 1:n
                                  Delta_T(Route(j),Route(j+1)) = Delta_T(Route(j),Route(j+1)) +D(Route(j),Route(j+1))* Q/Length(i);
                              end
                          end
                          T= (1-v) * T + Delta_T;
                                 % 迭代次数加1，并清空路径记录表
                        iter = iter + 1;
                        Table = zeros(m,n);              
end
%--------------------------------------------------------------------------
%% 结果显示
shortest_route=best_route(end,:);                 %选出最短的路径中的点
short_length=best_length(end);
Time_Cost=etime(clock,t0);
disp(['最短距离:' num2str(short_length)]);
disp(['最短路径:' num2str([shortest_route shortest_route(1)])]);
disp(['程序执行时间:' num2str(Time_Cost) '秒']);
%--------------------------------------------------------------------------
%% 绘图
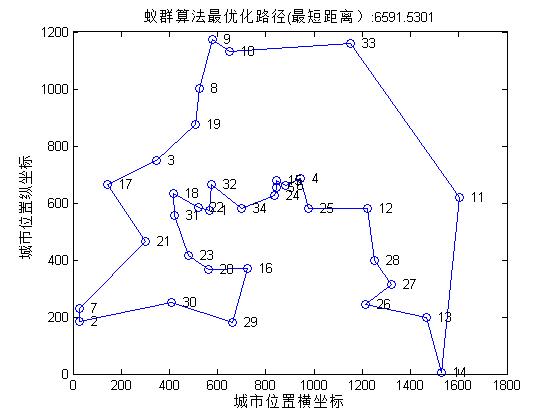
figure(1)
%采用连线图画起来
plot([city(shortest_route,1);city(shortest_route(1),1)], [city(shortest_route,2);city(shortest_route(1),2)],'o-');
for i = 1:size(city,1)
    %对每个城市进行标号
    text(city(i,1),city(i,2),['   ' num2str(i)]);
end
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法最优化路径(最短距离）:' num2str(short_length) ''])

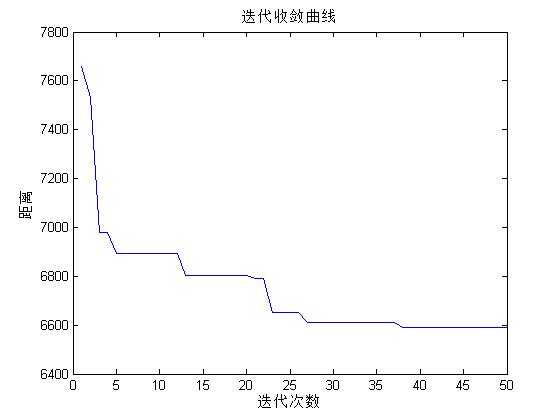
figure(2)
%画出收敛曲线
plot(1:iter_max,best_length,'b')
xlabel('迭代次数')
ylabel('距离')
title('迭代收敛曲线')

 

　程序说明：采用蚁群算法求取TSP问题，共有34个城市，从txt文件加载数据：

运行结果：