构造题-题单-思路

题单

图形构造

牛客练习赛106-D

传送门

思路

条件 n为奇数， 01数量相差为1，无回路， 1和1连通，0和0连通。

首先 该图可能满足 0 和 1在图中所构成的图形相同， 我们可以构造一个螺旋矩阵

但是螺旋矩阵中间的数无法填写， 因为会构成回路。

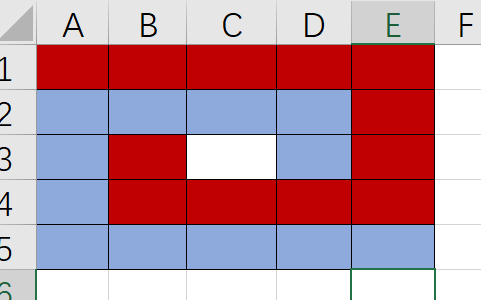
首先构成该图后，我们假设填入中间为红色，那么 对于红色和蓝色的任意次交换都不会改变其\(\lfloor \frac{n}{2} \rfloor + 1\) 和 \(\lfloor \frac{n}{2} \rfloor\) 的数量。

如果，我们填蓝色经过交换D3处和其有些对角线处元素，可以满足条件

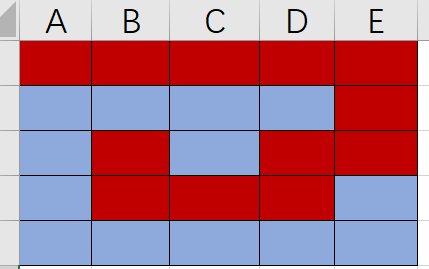
不失一般性， 对于任意大于3的奇数n我们都可以构造螺旋矩阵, 在中间填写上与其正上方或右侧相同颜色的元素， 那么对其右侧和下方连续交换直到不存在右侧下方元素，必然会得到满足该条件的矩阵，证略。

Code

#include <iostream>
#include <queue>
#include <vector>
#include <utility>
#include <cstring>
#include <stack>
#include <map>
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
const int N = 1e3 + 10;

int a[N][N], n;

void dfs(int x, int y, int dir, int len) {
	if (len == 1)
		return;
	if (dir == 0) { // 向右

		while (y < len) a[x][++y] = 1;
		dfs(x, y, 1, len - 1);

	} else if (dir == 1) { // 向下

		while (x < len) a[++x][y] = 1;
		dfs(x, y, 2, len);

	} else if (dir == 2) { // 向左

		while (y > n - len + 1) a[x][--y] = 1;	
		dfs(x, y, 3, len - 1);

	} else if (dir == 3) { // 向上

		while (x > n - len + 1) a[--x][y] = 1;
		dfs(x, y, 0, len);

	}
}

int main() {
	cin >> n;
	dfs(1, 0, 0, n);
	int mx, my, tx, ty;
	mx = my = n/2 + 1;
	tx = mx, ty = my + 1;
	a[mx][my] = a[mx-1][my];

	while (ty <= n && ty <= n) {
		swap(a[tx][ty], a[tx + 1][ty + 1]);
		tx ++, ty ++;
	}


	for (int i = 1; i <= n; i ++) {
		for (int j = 1; j <= n; j ++) {
			cout << a[i][j];
		}
		cout << endl;
	}
}