二叉树学习笔记

二叉树学习

​ 二叉树是，每个结点最多只有两个分支（即不存在分支度大于2的结点）的树结构。分支被称为“左子树”，“右子树”，顺序不能随意颠倒。二叉树的第i层至多拥有\(2^{i - 1}\) 个结点；深度为k的二叉树至多总共有\(2^{k} - 1\)个节点(定义根节点深度\(k_0 = 1\))， 对于任何一颗非空的二叉树\(T\), 如果其叶片（终端节点）数为\(n_0\), 分支度为2的节点数为\(n_2\), 则 \(n_0 = n_2 + 1\)(总结点数等于\(n = n_1 + n_2 + n_0 = 2n_2 + n_1 + 1\))

遍历

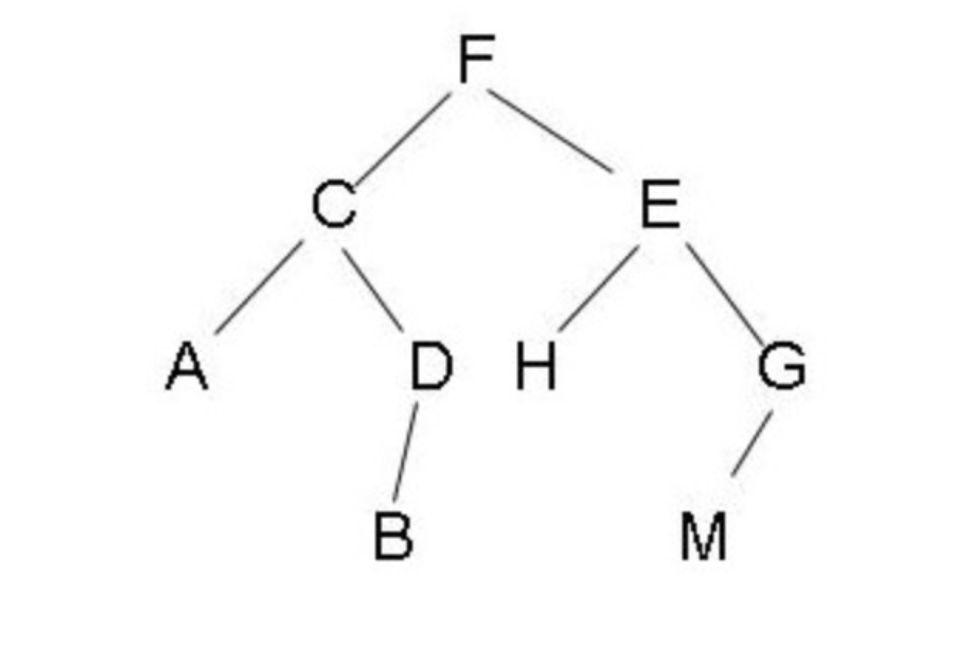
前序遍历

根左右，递归遍历

F C A D B E H G M

中序遍历

左根右，递归遍历

A C B D F H E M G

后序遍历

左右根，递归遍历

A B D C H M G E F

根据上面的遍历特点，总结一下的规律：

1. 左子树总是在右子树之前遍历
2. 中序遍历任取一点其左边必然是其左子树，右边必然是其右子树

建树

总结一下，其实根据先序（或后序）和中序是很好理解怎么建树的，但是判断推出条件很复杂，需要判断left（表示在中序中找根节点）是否没找到， 中序和先序（或后序）数组是否为空，长度len是否小于等于0来结束程序， 另外还需要给左右子树赋空值NULL

根据先序和中序建树

#include <iostream>
#include <cstdio>
#include <queue>

using namespace std;

typedef struct node {
    int data;
    struct node *lc, *rc;
}BiTree;

// 根据先序和中序建立一颗二叉树
void rebuild(int mid[], int order[], int len, BiTree* &root) {        //用引用传递指针, 避免双*使程序复杂
    if (len <= 0|| !mid || !order) return; // 判断长度是否合法, 中序序列是不为空, order 是不为空
    int left;

    for (left = 0; left < len; left ++) {
        if (mid[left] == order[0]) break; // 找到第一个相等的数值
    }

    if (left >= len) return; // 判断根节点是否在中序节点中

    root = new BiTree;
    root->data = order[0];
    root->lc = root->rc = NULL; // 左右子树赋为空, 防止随机地址造成if判断异常

    rebuild(mid, order + 1, left, root->lc); // 递归左子树

    rebuild(mid + 1 + left, order + 1 + left, len - left - 1, root->rc);  // 递归右子树

    // cout << root->data << endl;
}

根据后序和中序建树

#include <iostream>
#include <cstdio>
#include <queue>

using namespace std;

typedef struct node {
    int data;
    struct node *lc, *rc;
}BiTree;

int dep[100000];

// 根据后序和中序建立一颗二叉树
void rebuild(int mid[], int post[], int len, BiTree* &root) {
	if (len <= 0 || !mid || !post) return;
	int left;
	for (left = 0; left < len; left ++) {
		if (mid[left] == post[len - 1]) break;	
	}
	if (left >= len) return;
	root = new BiTree;
	root->data = mid[left], root->lc = root->rc = NULL;
	rebuild(mid, post, left, root->lc);
	rebuild(mid + left + 1, post + left, len - left - 1, root->rc);
}

int main() {
    int mid[7], post[7], last = 1;
    auto bfs = [&last](BiTree *p) {
        queue<BiTree*> q1;
        q1.push(p), dep[p->data] = 1;
        while (q1.size()) {
            auto t = q1.front(); q1.pop();
            if (dep[t->data] != last) {
                last = dep[t->data];
                cout << "\n";
            }
            cout << t->data << " ";
            if (t->lc) q1.push(t->lc), dep[t->lc->data] += dep[t->data] + 1;
            if (t->rc) q1.push(t->rc), dep[t->rc->data] += dep[t->data] + 1;
        }
    };
    for (int i = 0; i <= 6; i ++) {
        cin >> post[i];
    }
    for (int i = 0; i <= 6; i ++) {
        cin >> mid[i];
    }
    BiTree* root;
    rebuild(mid, post, 7, root);
    bfs(root);
}

分类

满二叉树

拥有当前深度下最多结点的二叉树，成为满二叉树

完全二叉树

深度为k有n个节点二叉树，当且仅当其中的每一个节点，都可以和深度k的满二叉树，序号从1到n的节点一一对应时，称为完全二叉树。