PTA-数塔

7-3 数塔

分数 30

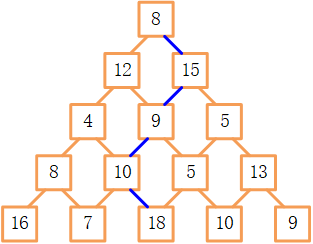
有一个N层数塔，顶层只有一个结点，每向下一层增加一个结点，最底层有N个结点(下图给出了一个5层数塔)。从顶层出发，每个结点可以选择向左下或者向右下行走，一直走到底层。要求找到一条路径，使得路径上的数值之和最大。例如，下图所示的5层数塔的最大和及其路径为：60=8+15+9+10+18。

输入格式:

输入在N+1进行，首先给出数塔的高度值N。接下来的N行输入数塔各层结点的值，第一行给出顶层结点的一个值，每向下一行增加一个值，每行的值之间用空格间隔。

输出格式:

按照如下格式输出最大值及其路径。
最大值[结点-->结点-->... ... -->结点]

输入样例:

5
8
12 15
4  9  5
8 10 5 13
16 7 18 10 9

输出样例:

60[8-->15-->9-->10-->18]

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

思路

\(dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + a[i][j]\)

另外因为可能有负数的情况，所以边界可能会出错，有两种解决方法

1. 将边界初始化为-INF

2. 倒序dp从底层向上dp

   那么我们的dp方程可以写成\(dp[i][j] = max(dp[i + 1][j + 1], dp[i + 1][j]) + a[i][j]\), 这样我们不会触碰到边界

回溯方法：

开个数组记录一下每一层的前驱节点, 然后递归访问

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

long long dp[1000][1000], a[1000][1000];

// dp[i][j] 表示第i层若选择该节点的最优解
// 则有 dp[i][j] = max(dp[i - 1][j + 1], dp[i - 1][j - 1]) + now

// 滚动
// for i in range(0, n):
// a[ti][j]

int b[9000][9000];

void out(int j, int i){
	if(j == 1) {
		cout << a[j][i];
	} else {
		out(j - 1, b[j][i]);
		cout << "-->" << a[j][i];
	}
}

int main() {
	int n; cin >> n;
	for (int i = 1; i <= n; i ++) {
		for (int j = i; j >= 1; j --) {
			cin >> a[i][j];
            if(dp[i - 1][j] > dp[i - 1][j - 1]) {
                b[i][j] = j;
                dp[i][j] = dp[i - 1][j] + a[i][j];
            }else {
                b[i][j] = j - 1;
                dp[i][j] = dp[i - 1][j - 1] + a[i][j];
            }
		}
	}
	long long ans = -1;
    int ai = 1;
	for(int i = 1; i <= n; i ++) {
		if (dp[n][i] > ans)
			ans = dp[n][i], ai = i;
	}
    cout << ans;
	cout << "[";
    out(n, ai);
    cout << "]";
}